如果S是复数那么1/S 在空间上的图形就是：既然是复数肯定含有相位角。所以图形是有复数的模和相位角共同组成的。
305f88f735894d1a8302a3698d3fd213~noop.image?_iz=58558&from=article.jpg

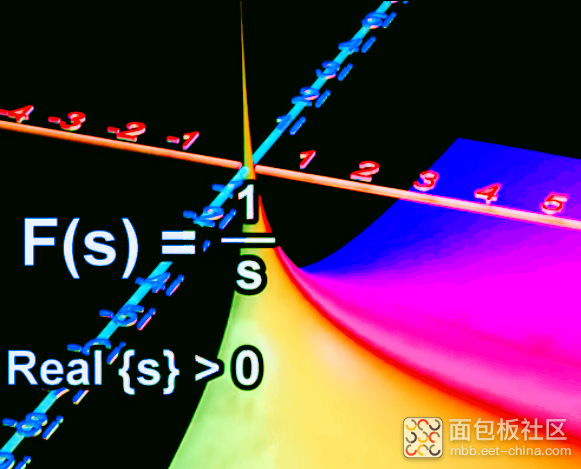
相位角的表示方法
c676d33e55694e82aec7483dac85d945~noop.image?_iz=58558&from=article.jpg

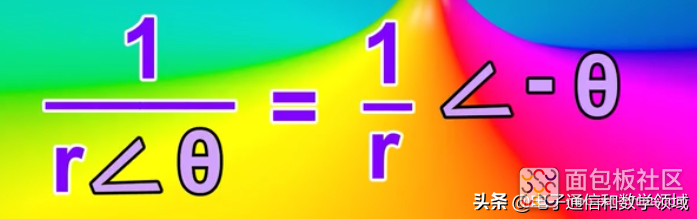
让任意一条线通过复平面的图形
5bb653d677fc4b77a5c5c49ca96a3da4~noop.image?_iz=58558&from=article.jpg

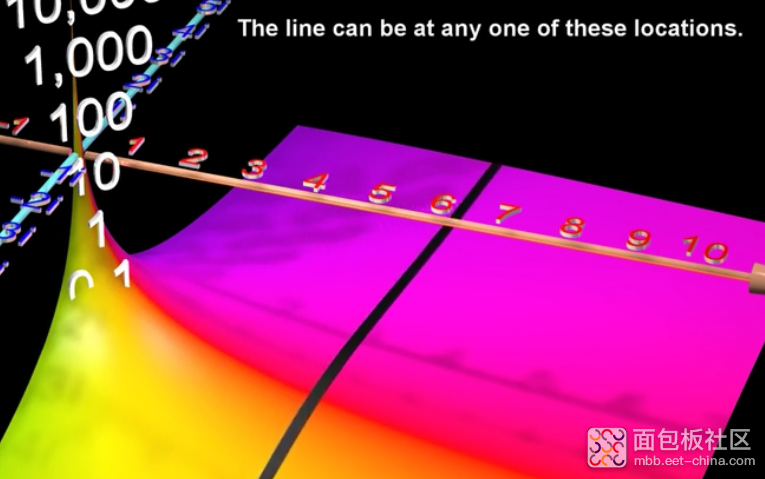
把这条线上的任意一点看做是复指数函数，那么这条线就被看所是复指数函数的叠加，叠加在一起就是一条波形
1f43a2feab9a4038bf95ff32f2e145f9~noop.image?_iz=58558&from=article.jpg

f48e13b82a284a6bab193bdeba3ef620~noop.image?_iz=58558&from=article.jpg

如下图每个时间点下的s都是一个常数，波形只不过是这些s为常数的复指数的累积，在复平面上的那条线可以看做如图波形
d12cc1acd5d7430097c2724eee0ddf52~noop.image?_iz=58558&from=article.jpg

所以F(S)乘以e^st就构成了以整个复平面为基础的旋转量，这一步很关键哦。
（这个类似于傅里叶级数中 c *e^it,c是旋转半径，e^it是1圈/秒时在单位圆上的位置）
这里只是将c换成了复平面F(S)，e^it换成了复指数e^st
6d802ce78e32485bbc559ff85c483d81~noop.image?_iz=58558&from=article.jpg

每个点之间的间距看做微元dx
77edd522414a456dabffd852242b550a~noop.image?_iz=58558&from=article.jpg

整个复指数的总和就是如下的公式
a3c7883849574f64999a67b7f98c7474~noop.image?_iz=58558&from=article.jpg

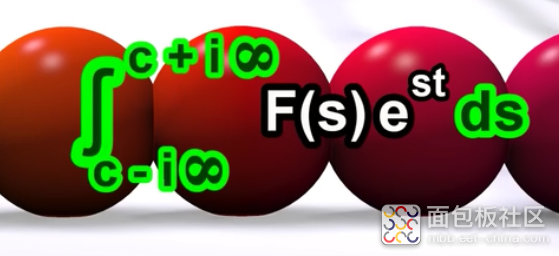
这样就得到原来创建的时间函数，其中c是常数。伙伴么你知道积分前面的常数怎么来的么？
8e1b5d5f889440caa9fd2db37a8d2fae~noop.image?_iz=58558&from=article.jpg

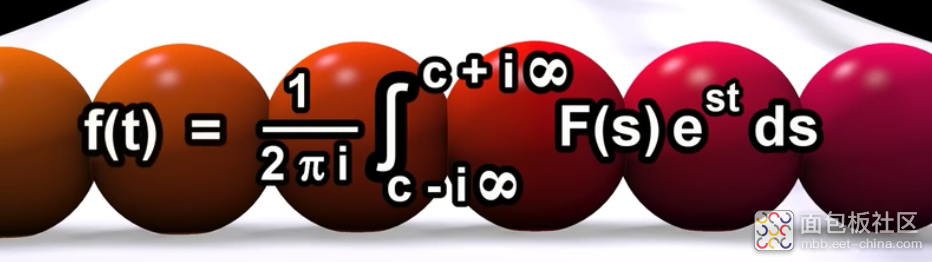
我们希望找到谁是f（t）的拉普拉斯变换，我们利用上式的原理乘以e^-st
图中用单位阶跃函数来表示f（t）就变成了
42129b206f3940a8a11a7bbd134723bf~noop.image?_iz=58558&from=article.jpg

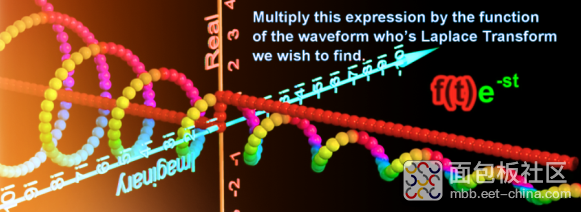
得到如图的模型，很明显乘积是个复数，每个点都用箭头表示
3ddc51d47c7e47c7b96fa587b676775f~noop.image?_iz=58558&from=article.jpg

将所有箭头叠加在一起
b5aa9ecb561e4106aef46e1466c0158a~noop.image?_iz=58558&from=article.jpg

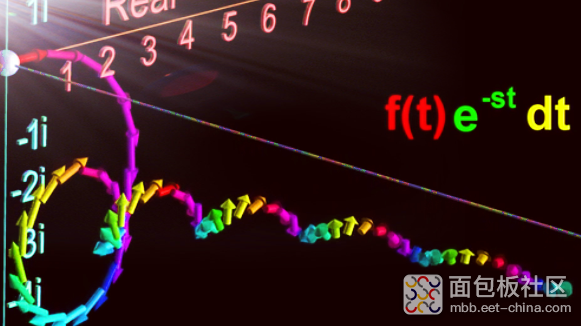
得到如图复数表示的拉普拉斯变换结果
cb7a0c86e49842d1bb46ccfcfbfa5c1a~noop.image?_iz=58558&from=article.jpg

上述就是整个拉普拉斯变换的原理与模型。非常直观也很容易理解。