比例,积分,微分的线性组合,构成控制量u(t),称为:比例(Proportional)、积分(Integrating)、微分(Differentiation)控制,简称PID控制
图1
控制器公式
在实际应用中,可以根据受控对象的特性和控制的性能要求,灵活地采用不同的控制组合,构成
比例(P)控制器
比例+积分(PI)控制器
比例+积分+微分(PID)控制器
式中
或
式中
控制系统中的应用
在单回路控制系统中,由于扰动作用使被控参数偏离给定值,从而产生偏差。自动控制系统的调节单元将来自变送器的测量值与给定值相比较后产生的偏差进行比例、积分、微分(PID)运算,并输出统一标准信号,去控制执行机构的动作,以实现对温度、压力、流量、也为及其他工艺参数的自动控制。
比例作用P只与偏差成正比;积分作用I是偏差对时间的积累;微分作用D是偏差的变化率;
比例(P)控制
比例控制能迅速反应误差,从而减少稳态误差。除了系统控制输入为0和系统过程值等于期望值这两种情况,比例控制都能给出稳态误差。当期望值有一个变化时,系统过程值将产生一个稳态误差。但是,比例控制不能消除稳态误差。比例放大系数的加大,会引起系统的不稳定。
图2比例(P)控制阶跃响应
积分(I)控制
在积分控制中,控制器的输出与输入误差信号的积分成正比关系。
为了减小稳态误差,在控制器中加入积分项,积分项对误差取决于时间的积分,随着时间的增加,积分项会增大。这样,即使误差很小,积分项也会随着时间的增加而加大,它推动控制器的输出增大使稳态误差进一步减少,直到等于零。
积分(I)和比例(P)通常一起使用,称为比例+积分(PI)控制器,可以使系统在进入稳态后无稳态误差。如果单独用积分(I)的话,由于积分输出随时间积累而逐渐增大,故调节动作缓慢,这样会造成调节不及时,使系统稳定裕度下降。
图3积分(I)控制和比例积分(PI)控制阶跃相应
微分(D)控制
在微分控制中,控制器的输出与输入误差信号的微分(即误差的变化率)成正比关系。
由于自动控制系统有较大的惯性组件(环节)或有滞后(delay)组件,在调节过程中可能出现过冲甚至振荡。解决办法是引入微分(D)控制,即在误差很大的时候,抑制误差的作用也很大;在误差接近零时,抑制误差的作用也应该是零。37ab9a9a-a2f0-476b-9c7f-dceaf7ce6bcc.JPG
图4微分 (D)控制和比例微分(PD)控制阶跃相应
总结:
PI比P少了稳态误差,PID比PI反应速度更快并且没有了过冲。PID比PI有更快的响应和没有了过冲。
图5
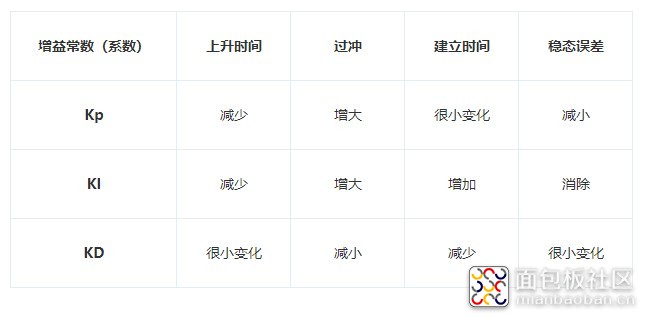
表1
注意,这里的
图6 典型的PID控制器对于阶跃跳变参考输入的响应
参数的调整
应用PID控制,必须适当地调整比例放大系数KP,积分时间TI和微分时间TD,使整个控制系统得到良好的性能。
最好的寻找PID参数的办法是从系统的数学模型出发,从想要的反应来计算参数。很多时候一个详细的数学描述是不存在的,这时候就需要实际地调节PID的参数.
Ziegler-Nichols方法
Ziegler-Nichols方法是基于系统稳定性分析的PID整定方法.在设计过程中无需考虑任何特性要求,整定方法非常简单,但控制效果却比较理想。
具体整定方法步骤如下:
1. 先置I和D的增益为0,逐渐增加KP直到在输出得到一个持续的稳定的振荡。
2. 记录下振荡时的P部分的临界增益Kc,和振荡周期Pc,代到下表中计算出KP,Ti, Td。
Ziegler-Nichols整定表
表2
Tyreus-Luyben 整定表:
表3
Tyreus-Luyben的整定值减少了振荡的作用和增强了稳定性。
自动测试方法:
为了确定过程的临界周期Pc和临界增益Kc,控制器会临时使它的PID算法失效,取而代之的是一个ON/OFF的继电器来让过程变为振荡的。这两个参数很好的将过程行为进行了量化以决定PID控制器应该如何整定来得到理想的闭环回路性能。
图6
51单片机PID算法程序(二)位置式PID控制算法
由51单片机组成的数字控制系统控制中,PID控制器是通过PID控制算法实现的。51单片机通过AD对信号进行采集,变成数字信号,再在单片机中通过算法实现PID运算,再通过DA把控制量反馈回控制源。从而实现对系统的伺服控制。
位置式PID控制算法
位置式PID控制算法的简化示意图
上图的传递函数为:
在时域的传递函数表达式
对上式中的微分和积分进行近似
式中n是离散点的个数。
于是传递函数可以简化为:
其中
u(n)——第k个采样时刻的控制;
KP ——比例放大系数;
Ki ——积分放大系数;
Kd ——微分放大系数;
T ——采样周期。
如果采样周期足够小,则(2-4)的近似计算可以获得足够精确的结果,离散控制过程与连续过程十分接近。
(2-4)表示的控制算法直接按(2-1)所给出的PID控制规律定义进行计算的,所以它给出了全部控制量的大小,因此被称为全量式或位置式PID控制算法。
缺点:
1)由于全量输出,所以每次输出均与过去状态有关,计算时要对e(k)(k=0,1,…n)进行累加,工作量大。
2)因为计算机输出的u(n)对应的是执行机构的实际位置,如果计算机出现故障,输出u(n)将大幅度变化,会引起执行机构的大幅度变化,有可能因此造成严重的生产事故,这在实际生产中是不允许的。
位置式PID控制算法C51程序
具体的PID参数必须由具体对象通过实验确定。由于单片机的处理速度和ram资源的限制,一般不采用浮点数运算,而将所有参数全部用整数,运算到最后再除以一个2的N次方数据(相当于移位),作类似定点数运算,可大大提高运算速度,根据控制精度的不同要求,当精度要求很高时,注意保留移位引起的“余数”,做好余数补偿。这个程序只是一般常用pid算法的基本架构,没有包含输入输出处理部分。
=====================================================================================================*/ #include <reg52.h> #include <string.h> //C语言中memset函数头文件 typedef struct PID { double SetPoint; // 设定目标Desired value double Proportion; // 比例常数Proportional Const double Integral; // 积分常数Integral Const double Derivative; // 微分常数Derivative Const double LastError; // Error[-1] double PrevError; // Error[-2] double SumError; // Sums of Errors } PID; double PIDCalc( PID *pp, double NextPoint ) { double dError, Error; Error = pp->SetPoint - NextPoint; // 偏差 pp->SumError += Error; // 积分 dError = Error - pp->LastError; // 当前微分 pp->PrevError = pp->LastError; pp->LastError = Error; return (pp->Proportion * Error // 比例项 + pp->Integral * pp->SumError // 积分项 + pp->Derivative * dError // 微分项 ); } void PIDInit (PID *pp) { memset ( pp,0,sizeof(PID)); } /*==================================================================================================== Main Program 主程序 =====================================================================================================* double sensor (void) // Dummy Sensor Function { return 100.0; } void actuator(double rDelta) // Dummy Actuator Function {} void main(void) { PID sPID; // PID Control Structure double rOut; // PID Response (Output) double rIn; // PID Feedback (Input) PIDInit ( &sPID ); // Initialize Structure sPID.Proportion = 0.5; // Set PID Coefficients sPID.Integral = 0.5; sPID.Derivative = 0.0; sPID.SetPoint = 100.0; // Set PID Setpoint for (;;) { // Mock Up of PID Processing rIn = sensor (); // Read Input rOut = PIDCalc ( &sPID,rIn ); // Perform PID Interation actuator ( rOut ); // Effect Needed Changes }
复制代码51单片机PID算法程序(三)增量式PID控制算法
当执行机构需要的不是控制量的绝对值,而是控制量的增量(例如去驱动步进电动机)时,需要用PID的“增量算法”。
增量式PID控制算法可以通过(2-4)式推导出。由(2-4)可以得到控制器的第k-1个采样时刻的输出值为:
将(2-4)与(2-5)相减并整理,就可以得到增量式PID控制算法公式为:
其中
由(2-6)可以看出,如果计算机控制系统采用恒定的采样周期T,一旦确定A、B、C,只要使用前后三次测量的偏差值,就可以由(2-6)求出控制量。
增量式PID控制算法与位置式PID算法(2-4)相比,计算量小得多,因此在实际中得到广泛的应用。
位置式PID控制算法也可以通过增量式控制算法推出递推计算公式:
增量式PID控制算法C51程序
/*====================================================================================================PID Function The PID (比例、积分、微分) function is used in mainly control applications. PIDCalc performs one iteration of the PID algorithm. While the PID function works, main is just a dummy program showing a typical usage. =====================================================================================================*/ typedef struct PID { int SetPoint; //设定目标 Desired Value long SumError; //误差累计 double Proportion; //比例常数 Proportional Const double Integral; //积分常数 Integral Const double Derivative; //微分常数 Derivative Const int LastError; //Error[-1] int PrevError; //Error[-2] } PID; static PID sPID; static PID *sptr = &sPID; /*==================================================================================================== Initialize PID Structure PID参数初始化 =====================================================================================================*/ void IncPIDInit(void) { sptr->SumError = 0; sptr->LastError = 0; //Error[-1] sptr->PrevError = 0; //Error[-2] sptr->Proportion = 0; //比例常数 Proportional Const sptr->Integral = 0; //积分常数Integral Const sptr->Derivative = 0; //微分常数 Derivative Const sptr->SetPoint = 0; } /*==================================================================================================== 增量式PID计算部分 =====================================================================================================*/ int IncPIDCalc(int NextPoint) { register int iError, iIncpid; //当前误差 iError = sptr->SetPoint - NextPoint; //增量计算 iIncpid = sptr->Proportion * iError //E[k]项 - sptr->Integral * sptr->LastError //E[k-1]项 + sptr->Derivative * sptr->PrevError; //E[k-2]项 //存储误差,用于下次计算 sptr->PrevError = sptr->LastError; sptr->LastError = iError; //返回增量值 return(iIncpid); }
复制代码1)Mixed-Signal Control Circuits Use Microcontroller for Flexibility in Implementing PID Algorithms,By Eamon Neary
2)Atmel 8-bit AVR Microcontrollers Application Note:AVR221: Discrete PID controller
3)使用Ziegler-Nichols方法的自整定控制 http://article.cechinamag.com/2007-03/200733042815.htm
4)Ziegler-Nichols Method http://www.chem.mtu.edu/~tbco/cm416/zn.html
5)Ziegler-Nichols方法PID参数整定--随风的blog http://blog.eccn.com/u/4/archives/2007/97.htm
6) PID控制原理教程,胡晓若编制
7)Atmel 8-bit AVR Microcontrollers Application Note:AVR221: Discrete PID controller
8)茶壶 - pid C程序,好东西 - 腾讯博客 – Qzone http://qzone.qq.com/blog/38162254-1225976777
9) PID 调节控制做电机速度控制,SUNPLUS凌阳科技
10)增量式PID控制模块程序设计 http://www.dzsc.com/data/html/2008-11-24/73560.html
作者 藤井树
原创文章,转载请注明出处
原帖地址:https://mbb.eet-china.com/blog/1315563-212882.html





 /5
/5 


