近几年,有几个被媒体大肆报道的事件,如下表所示。
如上所示,深度学习作为人工智能的一种具有代表性的实现方法,取得了很大的成功。那么,深度学习究竟是什么技术呢?深度学习里的“学习”是怎么做到的呢?为了解答这个疑问,我们需要先来了解一下神经网络,因为深度学习是以神经网络为出发点的。
神经网络的灵感来源谈到神经网络的想法,我们需要从生物学上的神经元(neuron)开始说起。从生物学扎实的研究成果中,我们可以得到以下关于构成大脑的神经元知识。
人的大脑是由多个神经元互相连接形成网络而构成的。也就是说,一个神经元从其他神经元接收信号,也向其他神经元发出信号。大脑就是根据这个网络上的信号的流动来处理各种各样的信息的。
神经元主要由细胞体、轴突、树突等构成。树突是从其他神经元接收信号的突起。轴突是向其他神经元发送信号的突起。由树突接收的电信号在细胞体中进行处理之后,通过作为输出装置的轴突,被输送到其他神经元。另外,神经元是借助突触结合而形成网络的。
让我们来更详细地看一下神经元传递信息的结构。如上图所示,神经元是由细胞体、树突、轴突三个主要部分构成的。其他神经元的信号(输入信号)通过树突传递到细胞体(也就是神经元本体)中,细胞体把从其他多个神经元传递进来的输入信号进行合并加工,然后再通过轴突前端的突触传递给别的神经元。
那么,神经元究竟是怎样对输入信号进行合并加工的呢?让我们来看看它的构造。
假设一个神经元从其他多个神经元接收了输入信号,这时如果所接收的信号之和比较小,没有超过这个神经元固有的边界值(称为阈值),这个神经元的细胞体就会忽略接收到的信号,不做任何反应。
注:对于生命来说,神经元忽略微小的输入信号,这是十分重要的。反之,如果神经元对于任何微小的信号都变得兴奋,神经系统就将“情绪不稳定”。
不过,如果输入信号之和超过神经元固有的边界值(也就是阈值),细胞体就会做出反应,向与轴突连接的其他神经元传递信号,这称为点火。
那么,点火时神经元的输出信号是什么样的呢?有趣的是,信号的大小是固定的。即便从邻近的神经元接收到很大的刺激,或者轴突连接着其他多个神经元,这个神经元也只输出固定大小的信号。点火的输出信号是由0 或1 表示的数字信息。
将神经元的工作在数学上抽象化,并以其为单位人工地形成网络,这样的人工网络就是神经网络。将构成大脑的神经元的集合体抽象为数学模型,这就是神经网络的出发点。
对于用神经网络实现的人工智能,人们只需要简单地提供数据即可。神经网络接收数据后,就会从网络的关系中自己学习并理解。如此看来,神经网络似乎有一些不可思议的逻辑。然而,从数学上来说,其原理十分容易。下面我们就一点点阐述它的原理。
神经网络中的数学一、神经元工作的数学表示
让我们先整理一下已经考察过的神经元点火的结构。
(i) 来自其他多个神经元的信号之和成为神经元的输入。
(ii) 如果这个信号之和超过神经元固有的阈值,则点火。
(iii) 神经元的输出信号可以用数字信号0 和1 来表示。即使有多个输出端,其值也是同一个。
下面让我们用数学方式表示神经元点火的结构。
首先,我们用数学式表示输入信号。由于输入信号是来自相邻神经元的输出信号,所以根据(iii),输入信号也可以用“有”“无”两种信息表示。因此,用变量x 表示输入信号时,如下所示。
注:与视细胞直接连接的神经元等个别神经元并不一定如此,因为视细胞的输入是模拟信号。
接下来,我们用数学式表示输出信号。根据(iii),输出信号可以用表示点火与否的“有”“无”两种信息来表示。因此,用变量y 表示输出信号时,如下所示。
最后,我们用数学方式来表示点火的判定条件。
从(i) 和(ii) 可知,神经元点火与否是根据来自其他神经元的输入信号的和来判定的,但这个求和的方式应该不是简单的求和。例如在网球比赛中,对于来自视觉神经的信号和来自听觉神经的信号,大脑是通过改变权重来处理的。因此,神经元的输入信号应该是考虑了权重的信号之和。
用数学语言来表示的话,例如,来自相邻神经元1、2、3 的输入信号分别为x1、x2、x3,则神经元的输入信号之和可以如下表示。
式中的w1、w2、w3 是输入信号x1、x2、x3 对应的权重(weight)。
根据(ii),神经元在信号之和超过阈值时点火,不超过阈值时不点火。于是,利用式(1),点火条件可以如下表示。
这里,θ 是该神经元固有的阈值。
例1
来自两个神经元1、2 的输入信号分别为变量x1、x2,权重为w1、w2,神经元的阈值为θ。当w1 = 5,w2 = 3,θ = 4 时,考察信号之和w1x1+ w2x2 的值与表示点火与否的输出信号y 的值。
二、点火条件的图形表示
下面我们将表示点火条件的式(2) 图形化。以神经元的输入信号之和为横轴,神经元的输出信号y 为纵轴,将式(2) 用图形表示出来。如下图所示,当信号之和小于θ 时,y 取值0,反之y 取值1。
如果用函数式来表示这个图形,就需要用到下面这个单位阶跃函数。
单位阶跃函数又称单位布阶函数,目前有三种定义,它们共同之处是自变量取值大于0时,函数值为1;自变量取值小于0时,函数值为0,不同之处是,自变量为0时函数值各不相同。
单位阶跃函数的图形如下所示。
利用单位阶跃函数u(z),式(2) 可以用一个式子表示如下。
通过下表可以确认式(3) 和式(2) 是一样的。
此外,该表中的z(式(3) 的阶跃函数的参数)的表达式
这称为该神经元的加权输入。
三、将神经元的工作一般化
上面为了接近神经元的形象,我们将神经元表示为了下图的样子。
然而,为了画出网络,我们需要画很多的神经元,在这种情况下上面那样的图就不合适了。因此,我们使用如下所示的简化图,这样很容易就能画出大量的神经元。
为了与生物学的神经元区分开来,我们把经过这样简化、抽象化的神经元称为神经单元(unit)。
将神经元的示意图抽象化之后,对于输出信号,我们也对其进行一般化。
上面我们提到,根据点火与否,生物学上的神经元的输出y 分别取值1 和0(下图)。
然而,如果除去“生物”这个条件,这个“0 和1 的限制”也应该是可以解除的。这时表示点火与否的下式(前边式(3))就需要修正。
这里,u 是单位阶跃函数。我们将该式一般化,如下所示。
这里的函数a 是建模者定义的函数,我们称为激活函数(activation function)。x1、x2、x3 是模型允许的任意数值,y 是函数a 能取到的任意数值。这个式(2) 就是今后所讲的神经网络的出发点。
注:虽然式(2) 只考虑了3 个输入,但这是很容易推广的。另外,式(1) 使用的单位阶跃函数u(z) 在数学上也是激活函数的一种。
请注意,式(2) 的输出y 的取值并不限于0 和1,对此并没有简单的解释。一定要用生物学来比喻的话,可以考虑神经单元的“兴奋度”“反应度”“活性度”。
我们来总结一下神经元和神经单元的不同点,如下表所示。
将神经元点火的式(1) 一般化为神经单元的激活函数式(2),要确认这样做是否有效,就要看实际做出的模型能否很好地解释现实的数据。实际上,式(2) 表示的模型在很多模式识别问题中取得了很好的效果。
四、神经单元的激活函数
Sigmoid 函数
神经单元激活函数的代表性例子是Sigmoid 函数σ(z),其定义如下所示。
关于这个函数,我们以后可以继续深入学习。这里,我们先来看看它的图形,Sigmoid 函数σ(z) 的输出值是大于0 小于1 的任意值。此外,该函数连续、光滑,也就是说可导。这两种性质使得Sigmoid 函数很容易处理。
右图是激活函数的代表性例子Sigmoid 函数σ(z) 的图形。除了原点附近的部分,其余部分与单位阶跃函数(左图)相似。Sigmoid 函数具有处处可导的性质,很容易处理。
单位阶跃函数的输出值为1 或0,表示点火与否。然而,Sigmoid 函数的输出值大于0 小于1,这就有点难以解释了。如果用生物学术语来解释的话,如上文中的表格所示,可以认为输出值表示神经单元的兴奋度等。输出值接近1 表示兴奋度高,接近0 则表示兴奋度低。
偏置
再来看一下激活函数的式(2)。
这里的θ 称为阈值,在生物学上是表现神经元特性的值。从直观上讲,θ表示神经元的感受能力,如果θ 值较大,则神经元不容易兴奋(感觉迟钝),而如果值较小,则神经元容易兴奋(敏感)。
然而,式(2) 中只有θ 带有负号,这看起来不漂亮。数学不喜欢不漂亮的东西。另外,负号具有容易导致计算错误的缺点,因此,我们将- θ 替换为b。
经过这样处理,式子变漂亮了,也不容易发生计算错误。这个b 称为偏置(bias)。
我们将式(4) 作为标准使用。另外,此时的加权输入z如下所示。
式(4) 和式(5) 是今后所讲的神经网络的出发点,非常重要。
另外,生物上的权重w1、w2、w3 和阈值θ( = - b)都不是负数,因为负数在自然现象中实际上是不会出现的。然而,在将神经元一般化的神经单元中,是允许出现负数的。
练习题
下图是一个神经单元。如图所示,输入x1 的对应权重是2,输入x2的对应权重是3,偏置是- 1。根据下表给出的输入,求出加权输入z 和输出y。注意这里的激活函数是Sigmoid函数。
请自行填写之后看下面答案。
解:结果如下表所示(式(3) 中的e 取e = 2.7 进行计算)。
备注
改写式(5)。
我们将式(5) 像下面这样整理一下。
这里增加了一个虚拟的输入,可以理解为以常数1 作为输入值(下图)。于是,加权输入z 可以看作下面两个向量的内积。
( w1,w2,w3,b)(x1,x2,x3,1)
计算机擅长内积的计算,因此按照这种解释,计算就变容易了。
神经网络作为本文的主题,它究竟是什么样的呢?下面让我们来看一下其概要。
五、神经网络
上面我们考察了神经单元,它是神经元的模型化。那么,既然大脑是由神经元构成的网络,如果我们模仿着创建神经单元的网络,是不是也能产生某种“智能”呢?这自然是让人期待的。众所周知,人们的期待没有被辜负,由神经单元组成的网络在人工智能领域硕果累累。
在进入神经网络的话题之前,我们先来回顾一下上面考察过的神经单元的功能。
将这样的神经单元连接为网络状,就形成了神经网络。它的连接方法多种多样,本文将主要考察作为基础的阶层型神经网络。
神经网络各层的职责
阶层型神经网络如下图所示,按照层(layer)划分神经单元,通过这些神经单元处理信号,并从输出层得到结果,如下图所示。
构成这个网络的各层称为输入层、隐藏层、输出层,其中隐藏层也被称为中间层。
各层分别执行特定的信号处理操作。
- 输入层负责读取给予神经网络的信息。属于这个层的神经单元没有输入箭头,它们是简单的神经单元,只是将从数据得到的值原样输出。
- 隐藏层的神经单元执行前面所复习过的处理操作(1) 和(2)。在神经网络中,这是实际处理信息的部分。
- 输出层与隐藏层一样执行信息处理操作(1) 和(2),并显示神经网络计算出的结果,也就是整个神经网络的输出。
人工智能中著名的深度学习,顾名思义,就是叠加了很多层的神经网络。叠加层有各种各样的方法,其中著名的是卷积神经网络。
从数学角度看神经网络的学习了解卷积神经网络可以阅读《卷积神经网络的Python实现》这本书。
关于神经网络的详细介绍,请看《这是我看过,最好懂的神经网络》这篇文章。
我们了解了神经网络识别输入图像的机制,。具体来说,就是根据神经单元中的权重关系来判断。那么,这个权重的大小是如何确定的呢?神经网络中比较重要的一点就是利用网络自学习算法来确定权重大小。
神经网络的参数确定方法分为有监督学习和无监督学习。本文只提到了监督学习,有监督学习是指,为了确定神经网络的权重和偏置,事先给予数据,这些数据称为学习数据。神经网络根据给定的学习数据确定权重和偏置,称为学习。
注:学习数据也称为训练数据。
那么,神经网络是怎样学习的呢?其实思路极其简单:计算神经网络得出的预测值与正解的误差,确定使得误差总和达到最小的权重和偏置。这在数学上称为模型的最优化(下图)。
关于预测值与正解的误差总和,有各种各样的定义。本文采用的是最古典的定义:针对全部学习数据,计算预测值与正解的误差的平方(称为平方误差),然后再相加。这个误差的总和称为代价函数(cost function),用符号CT 表示(T 是Total 的首字母)。
利用平方误差确定参数的方法在数学上称为最小二乘法,它在统计学中是回归分析的常规手段。
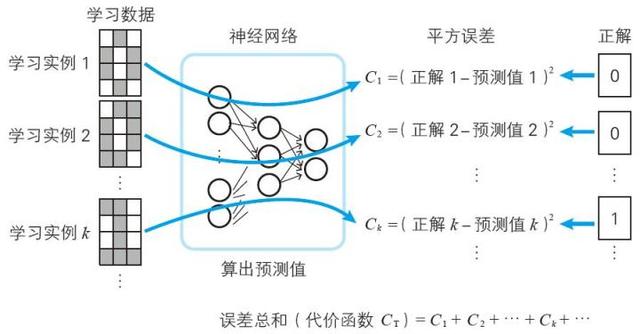
最优化是指确定使得误差总和最小的参数的方法。
来源:图灵教育《深度学习的数学》







 /2
/2 

