机器学习是什么,是用来干什么的?
机器学习就是样本中有大量的x(特征量)和y(目标变量)然后求这个function。
机器学习是让机器寻找函数Y=f(X)的过程,使得当我们给定一个X时,会返回我们想要得到的Y值。
例:
房价预测:X:位置、层数 -> Y:xxxx元/平
相亲预测:X:高富帅、矮矬穷 -> Y:见、不见
车牌识别:X:(车牌图片)-> Y:车牌号码
机器翻译:X:(中文) -> Y:(英文)
语音识别:X:(一段语音)-> Y:(一段文字)
聊天机器人:X:How are you -> Y:IM fine
一、机器学习
大致可以把机器学习分为Supervised learning(监督学习)和Unsupervised learning(非监督学习)两类。两者区别在于训练样本。
监督学习( supervised learning): 这种方法使用已标记数据来学习,它使用的标记数据可以是用户对电影的评级(对推荐来说)、电影标签(对分类来说)或是收入数字(对回归预测来说)。
无监督学习( unsupervised learning): 一些模型的学习过程不需要标记数据,我们称其为无监督学习。这类模型试图学习或是提取数据背后的结构或从中抽取最为重要的特征。
监督学习多用于回归分析(求解是连续值,比如某一区间)和分类问题(求解是离散值,比如对错)。非监督学习初步多用于聚类算法(群分析)。
1. 监督学习
1.1 回归分析
初识:
"回归于事物本来的面目"
出自高尔顿种豆子的实验,通过大量数据统计,他发现个体小的豆子往往倾向于产生比其更大的子代,而个体大的豆子则倾向于产生比其小的子代,然后高尔顿认为这是由于新个体在向这种豆子的平均尺寸"回归",大概的意思就是事物总是倾向于朝着某种"平均"发展,也可以说是回归于事物本来的面目。
进阶:
线性回归:
即y=ax+b,因变量和自变量为线性关系,输出y为一具体数值,例如房价预测中的房价,产量预测中的产量等等,主要用于预测某一具体数值。
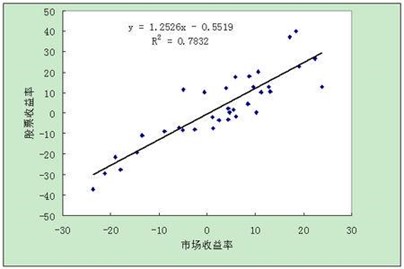
逻辑回归:
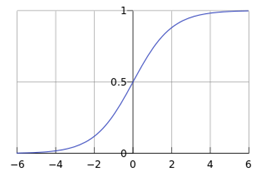
一个被logistic方程(sigmoid函数,如下图)归一化后的线性回归,将线性回归输出的很大范围的数,压缩到0和1之间,这样的输出值表达为某一类别的概率,主要用于二分类问题。
1.2 决策树
初识:
相亲预测:
决策树分类的思想类似于找对象。现想象一个女孩的母亲要给这个女孩介绍男朋友,于是有了下面的对话:
女儿:多大年纪了?
母亲:26。
女儿:长的帅不帅?
母亲:挺帅的。
女儿:收入高不?
母亲:不算很高,中等情况。
女儿:是公务员不?
母亲:是,在税务局上班呢。
女儿:那好,我去见见。
这个女孩的决策过程就是典型的分类树决策。相当于通过年龄、长相、收入和是否公务员对将男人分为两个类别:见和不见。
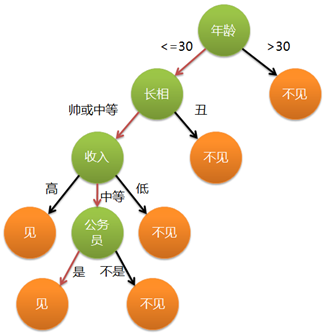
其中绿色节点表示判断条件,橙色节点表示决策结果,箭头表示在一个判断条件在不同情况下的决策路径。
进阶:
决策树(decision tree)是一个树结构。其每个非叶节点表示一个特征属性上的测试,每个分支代表这个特征属性在某个值域上的输出,而每个叶节点存放一个类别。使用决策树进行决策的过程就是从根节点开始,测试待分类项中相应的特征属性,并按照其值选择输出分支,直到到达叶子节点,将叶子节点存放的类别作为决策结果。
1.3 随机森林
初识:
"三个臭皮匠顶过诸葛亮"
随机森林中的每一棵决策树可以理解为一个精通于某一个窄领域的专家,这样在随机森林中就有了很多个精通不同领域的专家,对一个新的问题(新的输入数据),可以用不同的角度去看待它,最终由各个专家投票得到结果。

进阶:
随机森林通过自助法(bootstrap)重采样技术,从原始训练样本集N中有放回地重复随机抽取k个样本生成新的训练样本集合,然后根据自助样本集生成k个分类树组成随机森林,新数据的分类结果按分类树投票多少形成的分数而定。
随机森林可以用于分类和回归。当因变量Y是分类变量时,是分类;当因变量Y是连续变量时,是回归。
1.4 朴素贝叶斯
初识:
贝叶斯公式:
已知某种疾病的发病率是0.001,即1000人中会有1个人得病。现有一种试剂可以检验患者是否得病,它的准确率是0.99,即在患者确实得病的情况下,它有99%的可能呈现阳性。它的误报率是5%,即在患者没有得病的情况下,它有5%的可能呈现阳性。现有一个病人的检验结果为阳性,请问他确实得病的可能性有多大?
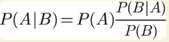
P(A|B)约等于0.019。也就是说,即使检验呈现阳性,病人得病的概率:也只从0.1%增加到了2%左右。这就是所谓的"假阳性",即阳性结果完全不足以说明病人得病。
进阶:
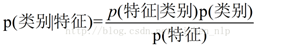
对于给出的待分类项,求解在此项特征出现的条件下各个类别出现的概率,哪个最大,就认为此待分类项属于哪个类别。
比如输入法里的错拼也能搜出正确的词,根据输入的字母及其周边可能出现的字母出现的概率,推荐出最符合想输入的词组。
1.5 支持向量机
初识:
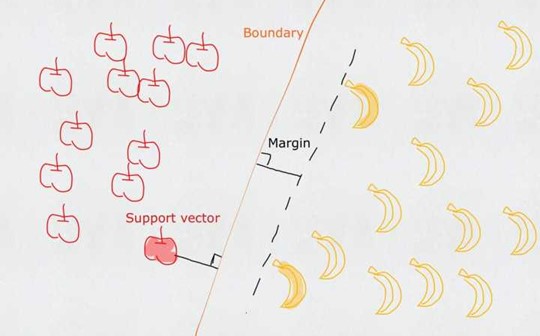
一个普通的支持向量机(SVM)就是一条直线,用来完美划分线性分割的两类。但这又不是一条普通的直线,这是无数条可以分类的直线当中最完美的,因为它恰好在两个类的中间,距离两个类的点都一样远。而所谓的支持向量就是这些离分界线最近的『点』。如果去掉这些点,直线多半是要改变位置的。可以说是这些vectors(主,点)support(谓,定义)了machine(宾,分类器)。
进阶:
在线性不可分的情况下,支持向量机通过某种事先选择的非线性映射(核函数)将输入变量映射到一个高维特征空间,在这个空间中构造最优分类超平面。

2. 非监督学习
2.1 Kmeans
初识:
"人以类聚,物以群分"
例:你左手在地上撒一把盐,右手在地上撒一把糖。假设你分不清盐和糖,但是你分别是用左右手撒的,所以两个东西位置不同,你就可以通过俩玩意的位置,判断出两个东西是两类(左手撒的,右手撒的)。然而能不能区别出是糖还是盐?不行。你只能分出这是两类而已。但是分成两类以后再去分析,就比撒地上一堆分析容易多了。
聚类分析主要就是把大类分为小类,然后再人工的对每一小类进行分析。
进阶:
K-均值是把数据集按照k个簇分类,其中k是用户给定的,其中每个簇是通过质心来计算簇的中心点。
首先创建一个初始划分,随机地选择 k 个对象(中心点),每个对象初始地代表了一个簇中心。对于其他的对象,根据其与各个簇中心的距离,将它们赋给最近的簇,然后重新计算簇的平均值,将每个簇的平均值重新作为中心点,然后对对象进行重新分配。这个过程不断重复,直到没有簇中对象的变化。
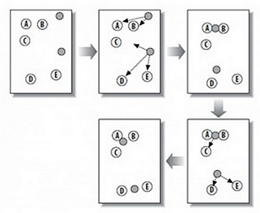
上图中,A,B,C,D,E是五个聚类点,灰色的点是质心点,聚为两类。
(1)随机在图中取K(这里K=2)个种子点。
(2)然后对图中的所有点求到这K个种子点的距离,假如点Pi离种子点Si最近,那么Pi属于Si点群。(上图中,我们可以看到A,B属于上面的种子点,C,D,E属于下面中部的种子点)
(3)接下来,我们要移动种子点到属于他的"点群"的中心。(见图上的第三步)
(4)然后重复第2)和第3)步,直到,种子点没有移动(我们可以看到图中的第四步上面的种子点聚合了A,B,C,下面的种子点聚合了D,E)。
版权声明:本文为CSDN博主「ukakasu」的原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/ukakasu/article/details/80015546







 /4
/4 

