在一个完美的世界里,我想要6英尺高,聪明,英俊;不幸的是,正如我妻子所证明的,我不符合这些条件。在信号完整性方面,S参数也是如此。在大多数情况下(不总是),当我们看到一条平滑的曲线,在频域中表现得很好而没有波纹时,我们觉得世界是安全的。另一方面,当我们看到奇怪的共振物质或S参数中的大幅度下降/峰值时,我们会感到疑惑和自问:到底发生了什么?(中间有几个形容词)。
让我们快速看一下图1。我敢说蓝色曲线很美,但红色锯齿状曲线很糟糕。正如你可能已经猜到的,蓝色曲线是一条很好的传输线,红色曲线是相同长度的线,上面叠加了一些半波共振。我们稍后再谈这个。
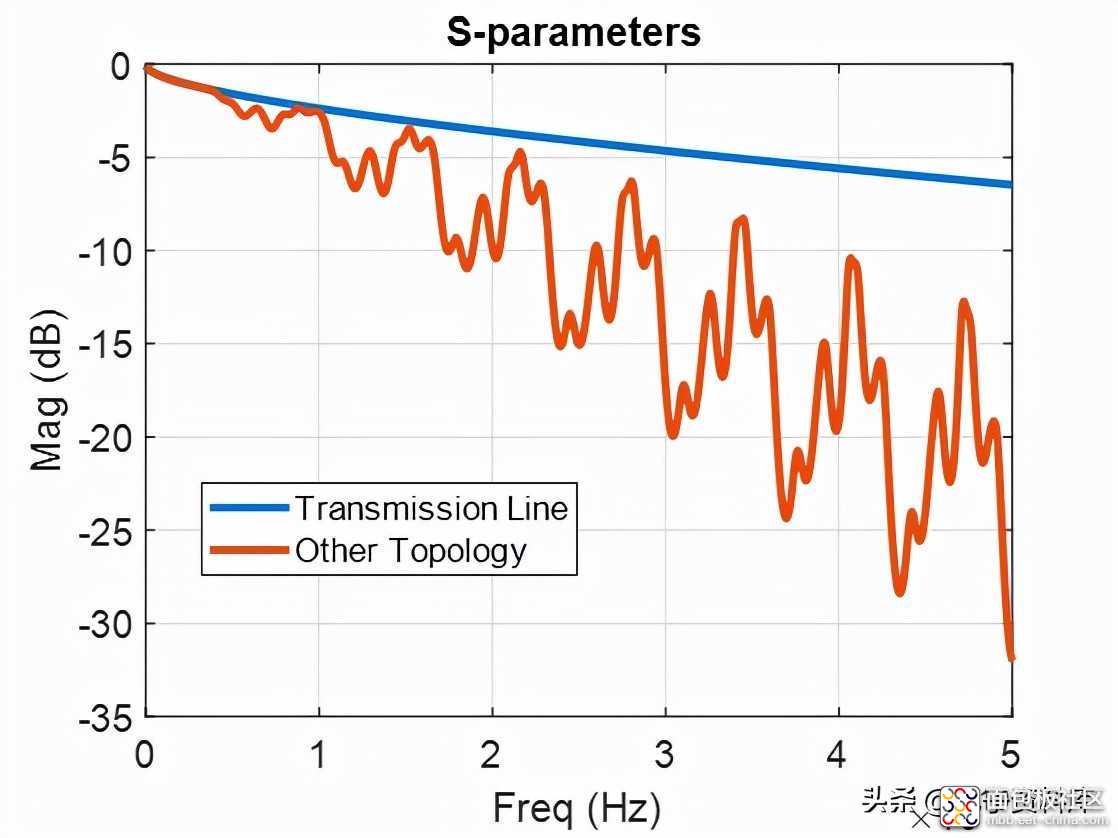
图1:输电线路与复杂拓扑S参数
这些年来,我逐渐意识到,特别是在信号完整性方面,半波共振通常是导致S参数变差的原因。你可以说任何类型的共振都会引起问题,你是对的。然而,在波的条件中,很容易形成共振,这是很有必要的。
也许解释半波共振产生的必要条件的最简单的方法是通过图2中的插图。想象两个孩子在荡绳子。靠近他们的手,他们将需要移动一点绳子,以刺激它,使它上下摆动。在孩子们中间,就在中间,绳子摆动得最厉害,达到顶峰。在这个类比中,把绳子想象成可能发生的任何其他振荡的包络,但不能超出这个包络。
你马上就会意识到绳子的形状类似于一个完整波形的一半,或者换句话说,整个波形需要一个等于两个孩子之间距离的距离。
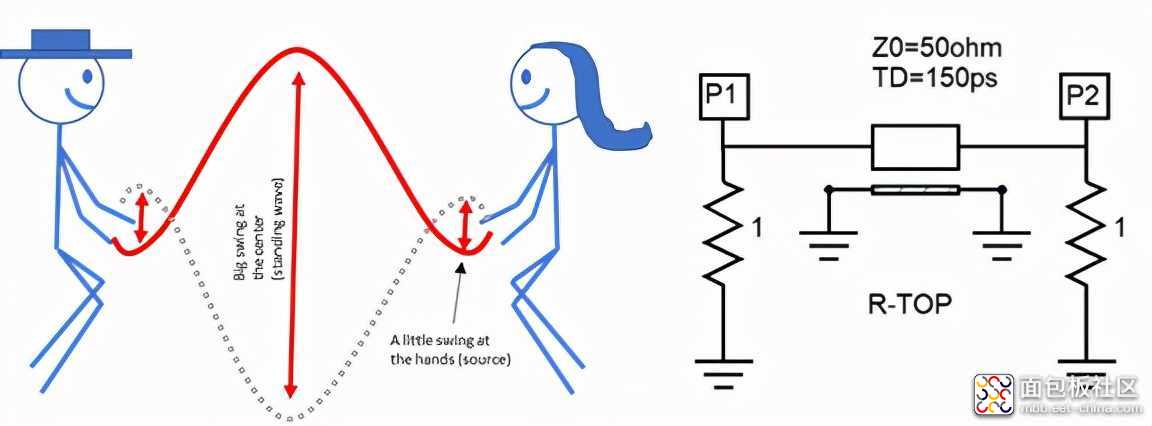
图2:半波共振基本原理
如图2所示,电路类比是显而易见的。我们把孩子们之间的距离表示为我们的传输线。事实上,孩子们有一只几乎不动的手,两端的终端,端口P1和P2作为源,或者孩子们用来移动绳子的力。你看,不管绳子有多大,都要甩在孩子的手上,它也不会,因为孩子们都在拉它,把它稳住。在绳子的中心,情况是非常不同的;绳子可以随意移动。
总之,要发生半波共振,我们需要满足以下条件:
- 两个终端/不连续同类的(相似但不一定相同),被电距离隔开
- 一种具有一定延迟的传输线介质,用于分离终端。
- 两端终端的阻抗与传输线特性阻抗不同这允许我们称端部终止不连续。

既然我们知道了半波共振发展所需的条件,我想回到以前的观点。为什么它们在信号完整性拓扑中如此常见?
一般来说,将SI拓扑想象成某种统一基带传输框架的方法之一是将其视为使用不同组件填充的某种统一基带传输框架(参见图3)。任何东西都可以构成一个组件,从直流屏蔽帽到各种连接器、电缆等。通常,当我们将这些组件连接到基带拓扑结构时,两端的连接大致相同,产生类似的不连续性。如果我们认为大多数元件/元件都有某种固有的延迟或电长度,我们就会意识到我们完全满足半波共振发生的条件,这就是为什么,只需简单地沿互连放置元件就可以促进半波共振。
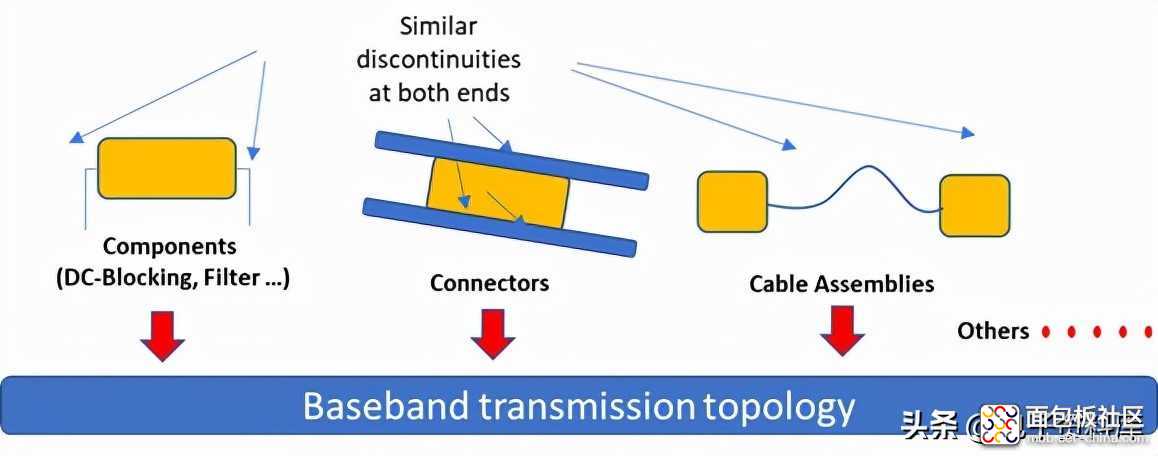
图3:拓扑结构
你可能会很快想到:“如果每一次我需要创建一个复杂的拓扑,我会有这些讨厌的半波共振,我是注定的!”好吧,是与否。正如你所想象的,就像SI中的每一件事一样,都有最小化它的方法,你会看到这些共振的程度会根据不同的情况而变化。我们稍后再讨论这个问题。
让我们回到图1,进一步分析锯齿线。图4是放大版,我们可以识别出两个共振。

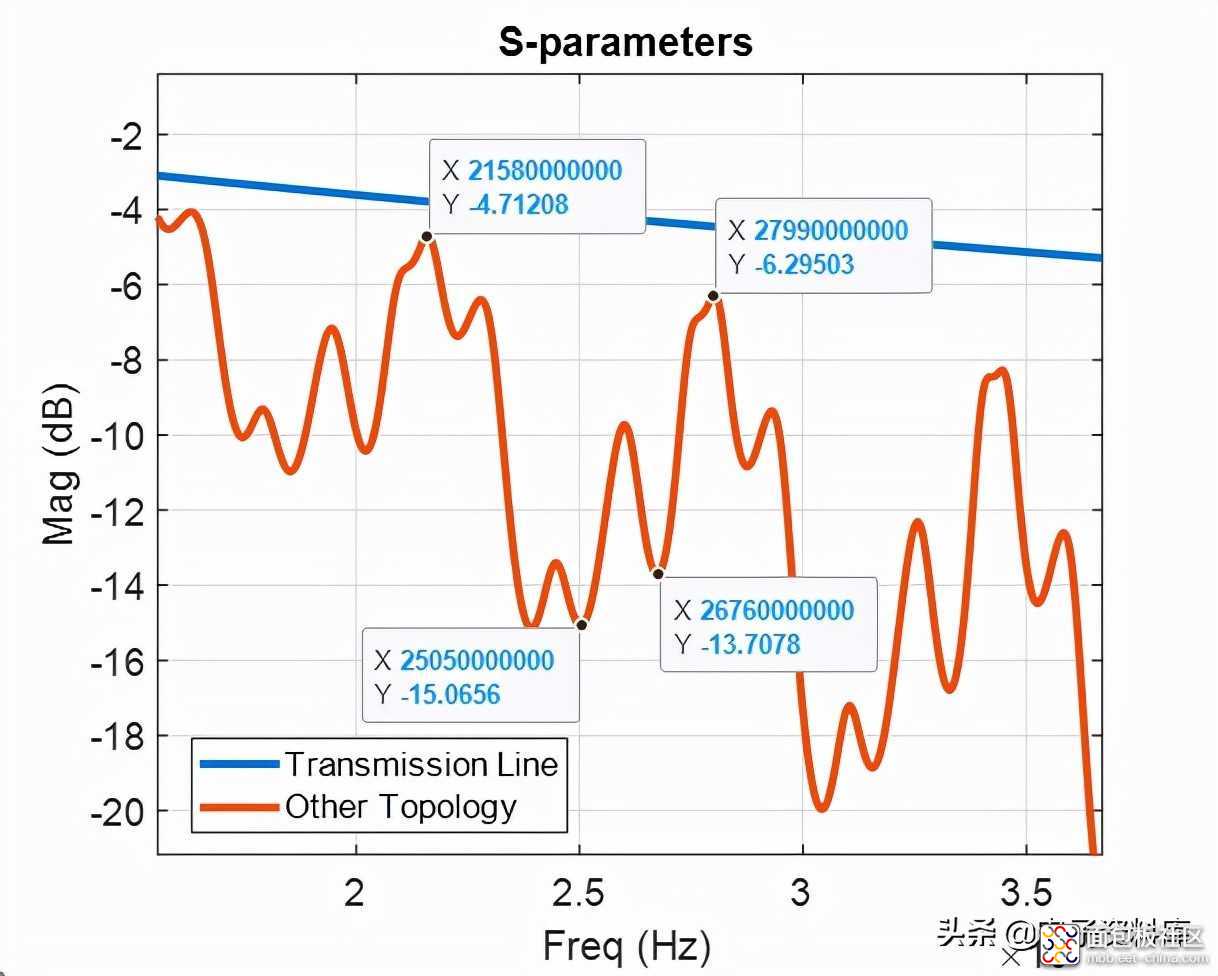
图4:双共振神秘拓扑
假设我们知道红色曲线代表一个复杂的拓扑,每单位长度的基带传输延迟为153ps/in
通过观察曲线和所有共振,我们怀疑它很可能有几个不连续性。有了这个框架,我们想看看我们能否确定这些不连续性之间的分离只要看看S参数的插入损耗。通过回顾跳绳儿童的例子,我们得出结论,所形成的共振是半波共振。(这意味着全波将是两个孩子之间距离的两倍。)在电路世界中,我们将用电长度代替单词distance,并且从数学上我们可以将测量到的谐振频率转换为距离,如下所示:
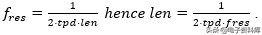
如果我们大致知道传输线的传播延迟,在我们的例子中
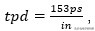
然后只要简单地看一下频域,我们就可以计算出不连续之间的近似长度。
让我们这样做:
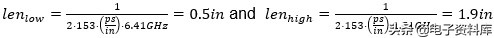
本质上只要看频域S参数,如果我们假设只有½波共振我们可以估计应该有两组不连续性,一组0.5in,另一组以大约2in。
图5显示了生成前面显示的红色曲线的神秘拓扑。如您所见,这是一个简化的行为拓扑,传输线具有不同的长度,但具有相同的特性阻抗
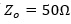
单位长度传播延迟
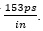
此外,拓扑结构具有集中元素,可以表示不同组件的附着不连续性。
这个拓扑非常简单,只是为了说明这一点,但是请注意,在更复杂的拓扑中,完全相同的行为也会发生。例如,与0.5in,当你有一个75ps
连接器两端连接的通孔未正确调整。
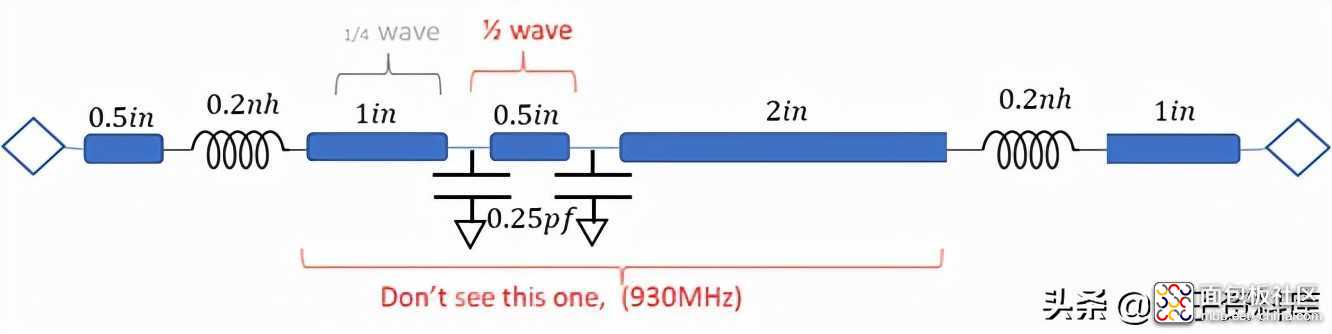
图5:神秘拓扑图
最终通过分析频域,我们能够正确地识别出最强的共振flow,较小的fhigh
共振来自于另一种被称为¼波共振的共振,这是未来文章的主题。我们注意到两个电感器之间的相互作用(同一类型的不连续性)不容易被发现,或者它被其他更大的共振严重掩盖和衰减。
主要的一点是,有了这些知识和使用一个非常简单的公式,我们可以尝试跟踪和最小化共振。
但是,等等,到目前为止,我们已经讨论过如何识别电路中的半波共振,这也是战斗的一部分,但是我们没有提到如何最小化它们。
共振抑制有两种基本方法可以最小化这些共振:
- 减小不连续性幅值(末端反射)
- 增加不连续性之间的损失
为了说明这一点,我将作弊并使用
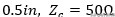
传输线拓扑,但我将用
forty
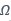
重整化阻抗如图6所示。

图6:40Ω的简单输电线路
使用与传输线不同的重整化阻抗Z0
以最简单的方式为½波共振的发展创造了合适的条件。请注意,我们在末端有两个不同于传输线特性阻抗的终端,在末端产生两个相等的反射,并满足半波共振产生的条件。
关于使用S参数重整化阻抗对我们有利的更深入的讨论可以在上一篇文章中找到,S参数重整化,作弊的艺术 ” [1].
如前所述,不断增加的损失往往会使这些共振的影响最小化。
我们可以设想两种增加损耗的方法,一种是改变介质(如改变损耗正切),另一种是增加介质长度0.5in
输电线路如图6所示
记住,通过损耗正切改变损耗不改变传输线端到端的总延迟,这意味着频域中的共振周期将保持不变。另一方面,改变输电线路的长度,是否会改变端到端的总延迟因此,半波共振的共振周期将发生变化。
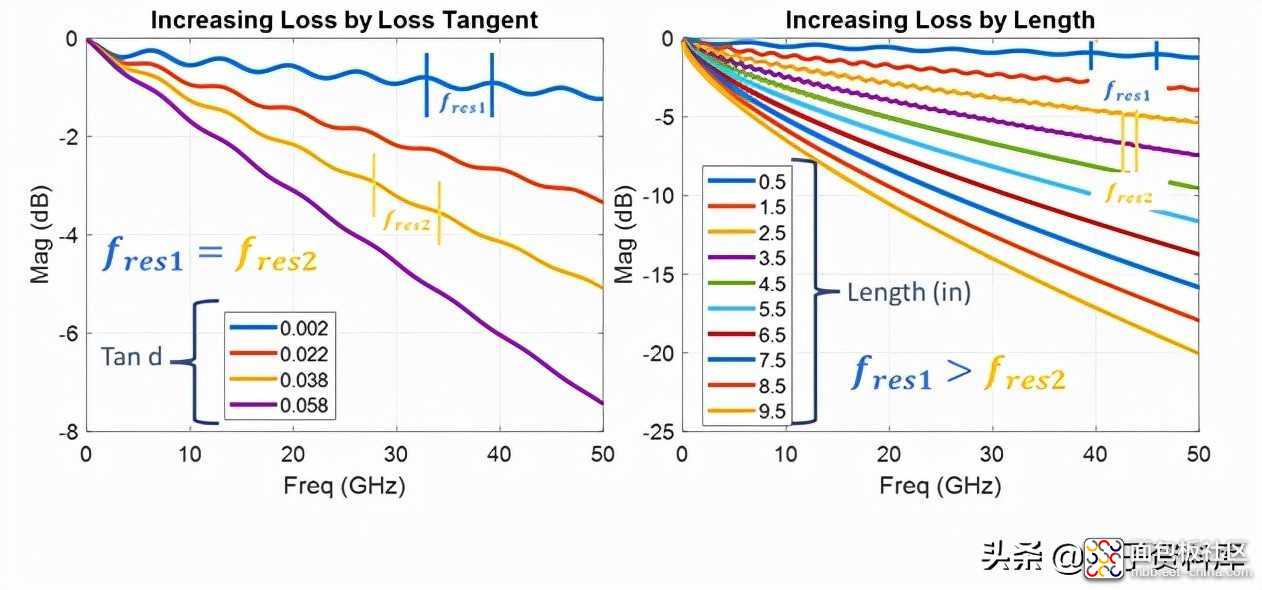
图7:通过增加损耗减少不连续性:(左)增加损耗正切,(右)增加tan d=0.002的长度
如图7所示,当我们通过增加损耗角正切来增加损耗时,谐振频率保持不变,但是随着损耗的增加,共振会受到更多的抑制。另一方面,当我们通过增加长度和使用非常低的介电损耗来增加损耗时,
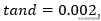
我们看到两个影响:阻尼衰减和共振频率随着不连续间隔的增加而变化。
当目测图7的右侧时
当然,频率比
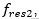
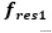
所以
我为什么要说
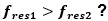
对于工程师来说,这是一个常见的混淆点。请注意,我们正在测量一个频率在频率轴上,本质上是一个频率的频率(这被称为倒谱),这就是为什么它令人困惑。要想放松自己,只需测量连续峰值上的频率值,然后减去。在本文前面提到图4时,已经展示了这一点。当你这么做的时候,你会看到的
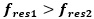
.让我们继续讨论最小化这些半波共振的最明显的方法。
我们知道要得到共振,我们必须有在两端产生反射的不连续,所以最小化半波共振的明显方法就是最小化这些不连续/反射。
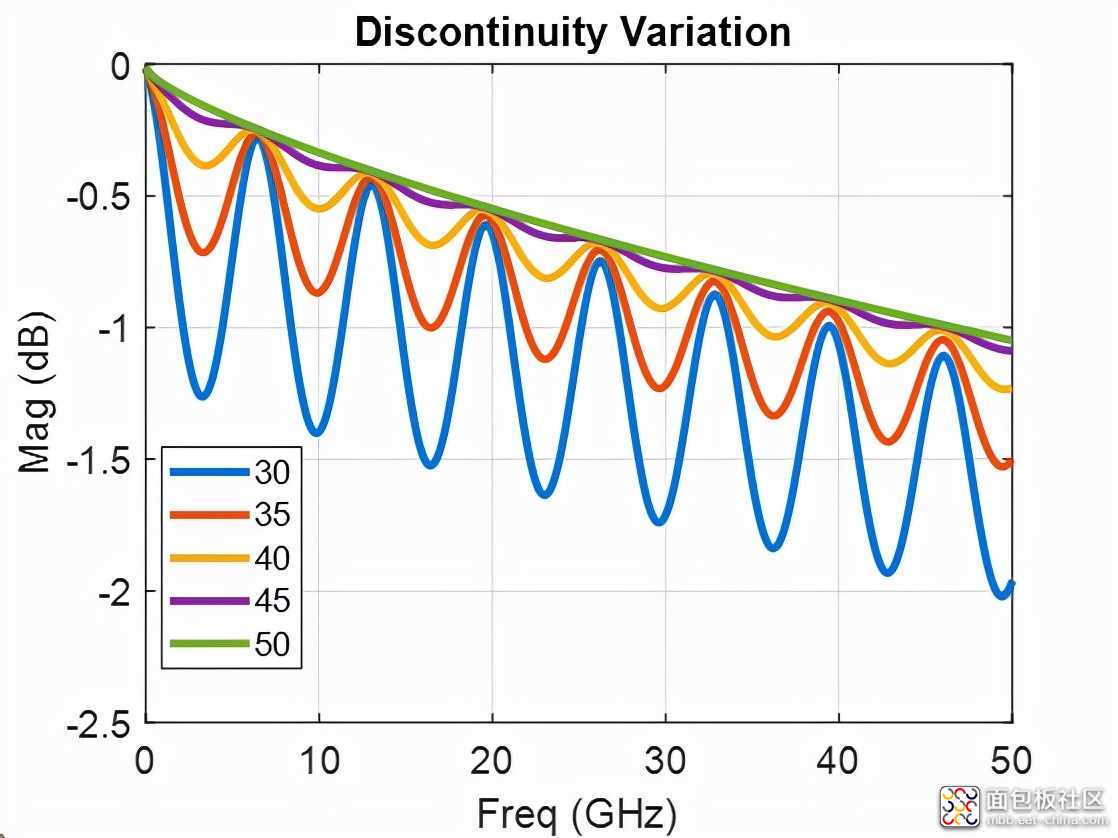
图8:阻抗幅值引起的共振振幅变化
在图8中,我们使用了图6所示的相同拓扑,并且通过改变S参数重整化阻抗
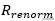
更接近
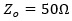
,反射越小,情况就越变越好。
最后,什么时候
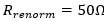
没有反射,半波共振消失。
这是一个非常简单的方法来说明反射的大小如何影响这些半波共振的整体大小。在实际的拓扑结构中,当元件的连接设计不当,并且连接的阻抗与分离连接的介质的阻抗相差很大时,这种情况经常发生。
来源:电子资料库







 /3
/3 
