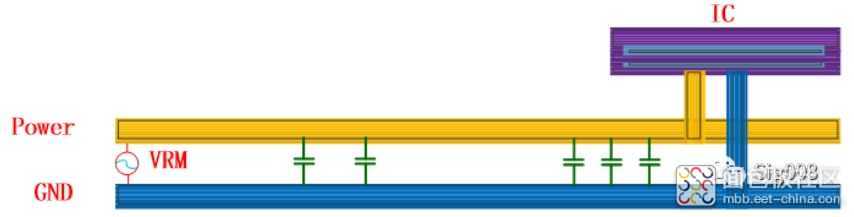
电容在PDN(power distribution network)当中的示意图
想要知道电容如何降低PDN阻抗,首先就要知道电容自身的阻抗特性,自身寄生参数的影响。
话不多说,首先思考一下,纯电容的阻抗是什么样的?
我们可能会想到这样一个公式:
Z=1/(2*pi*f*c)
没错,可是这样不太能帮助我们理解电容在PDN中起到的作用,还不够直观;
我们再思考一下,如果画一个电容的阻抗 VS 频率的曲线会是什么样的呢?
如下图:
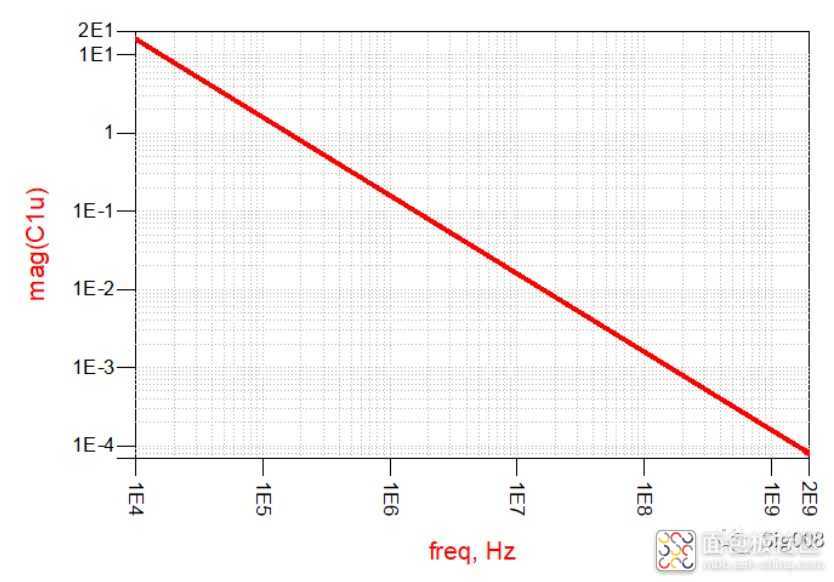
这就是纯电容的阻抗 VS 频率曲线,在曲线中我们可以直观的看出电容阻抗和频率的关系;
下面再来看一下不同容值电容的阻抗曲线:
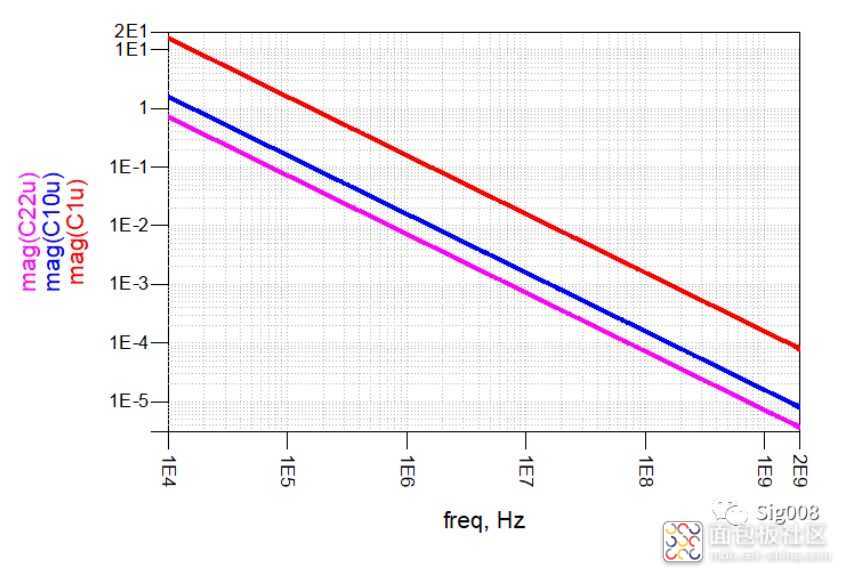
容值越大,阻抗越小,整个曲线表现为整体向下平移;
正因为电容对于高频信号表现为低阻抗特性,因此,在PDN系统中加了很多去耦电容,但是,我们已经介绍过,电容当中还有寄生电感(ESL)和等效串联电阻(ESR),所以我们还得研究寄生参数的影响;
下面,我们来看一下,纯电感的阻抗特性,公式如下;
Z=2*pi*L*f
同样,我们也看一下电感的阻抗 VS 频率的曲线:
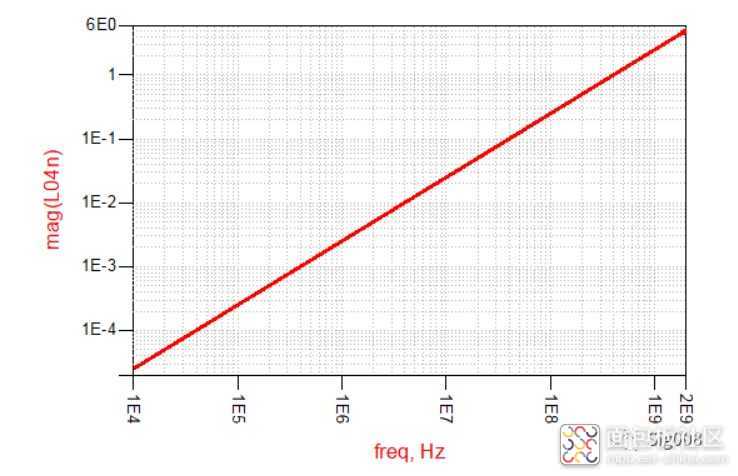
通过曲线,可以直观看到,电感的阻抗随频率的变化关系;
下面看一下,不同电感值的阻抗曲线,相信此时大家已经有了直观的印象,可以脑补出不同电感的曲线了:
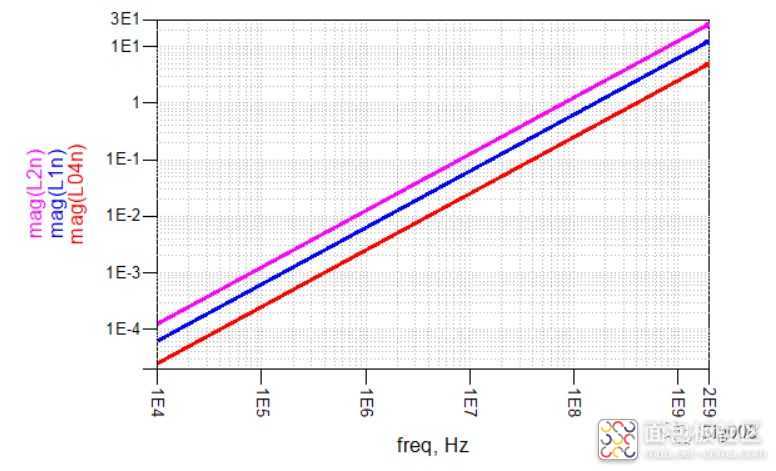
下面该电阻了,纯电阻的阻抗 VS 频率曲线如下:
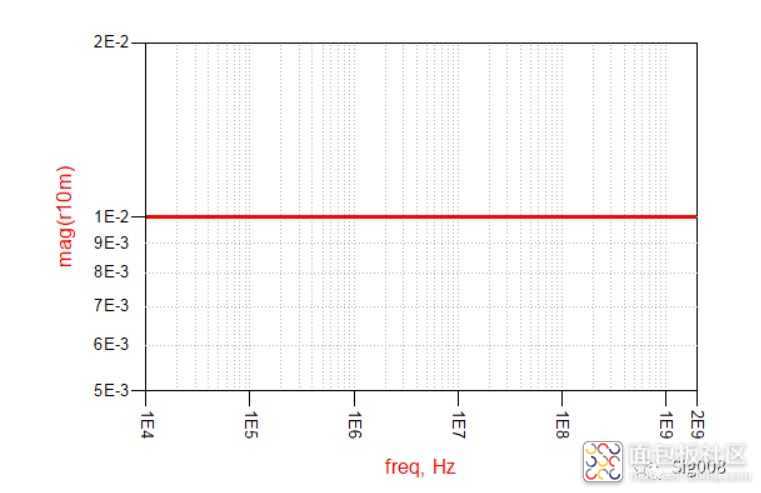
这个没什么好说的了,往下看
下面重点来了
单个器件的阻抗特性知道了,那么他们串联之后是什么样的呢,下面请看电阻和电容串联:
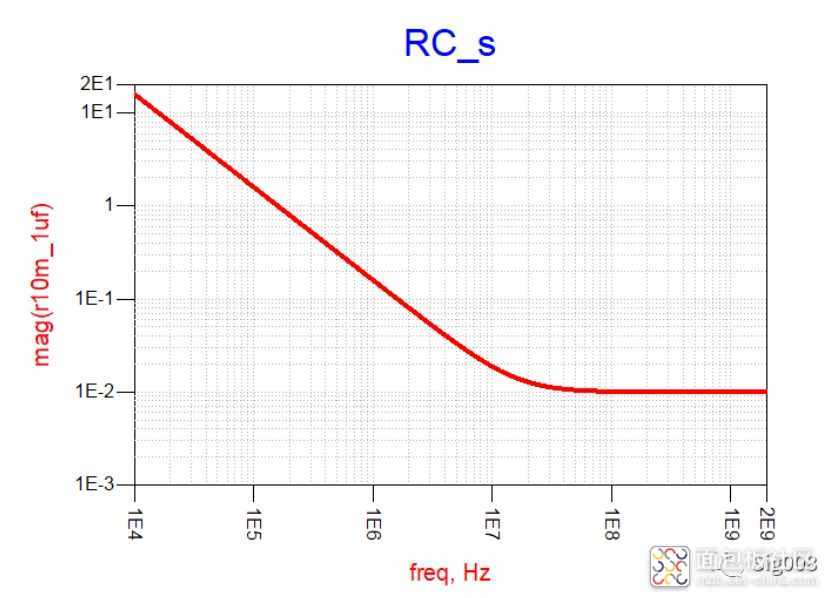
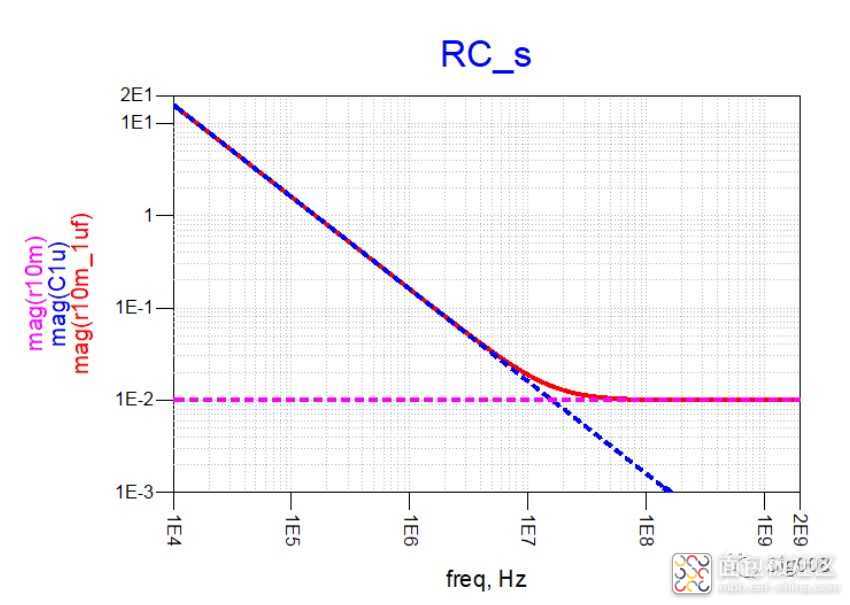
可以看到,RC串联后,低频部分阻抗呈现荣性,大小就是串联电容的阻抗大小,高频部分为阻性,大小为电阻的阻抗大小,下面请看电阻和电感串联:
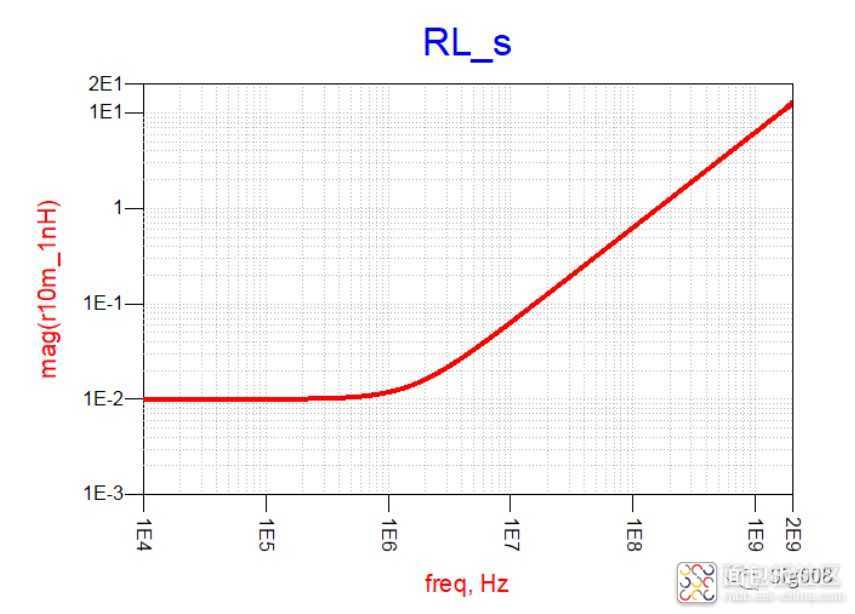
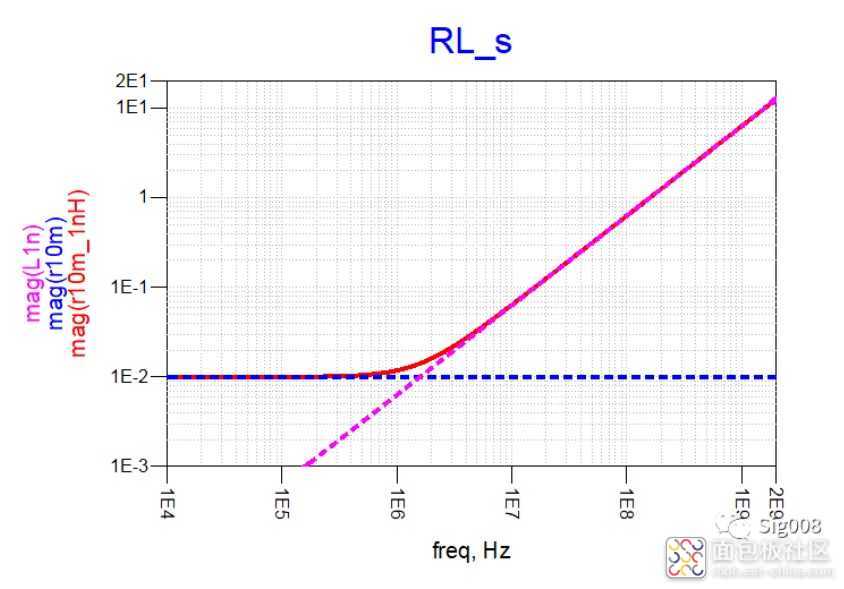
可以看到,RL串联后,低频部分阻抗呈现为阻性,大小为电阻的阻抗大小,高频部分阻抗呈现感性,大小就是串联电感的阻抗大小,下面请看电容和电感串联:
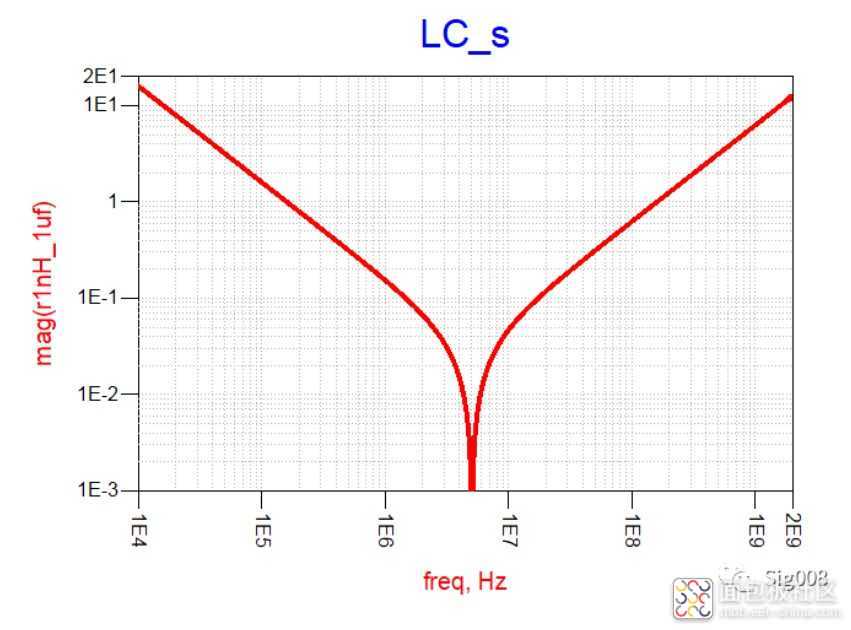
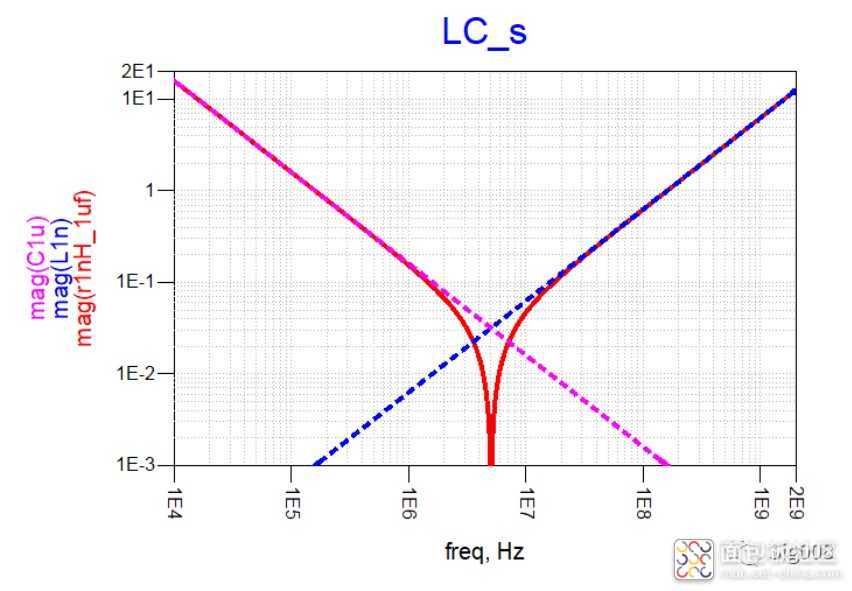
可以看到,LC串联后,低频部分阻抗呈现为容性,大小为电容的阻抗大小,高频部分阻抗呈现感性,大小就是串联电感的阻抗大小,而不同于与电阻串联的一点就是,LC串联会形成谐振,谐振点的频率可以这样计算:
在谐振点处,电容的阻抗值等于电感的阻抗值,即
Z=1/(2*pi*f*c)=2*pi*L*f
推导出f=1/(2*pi*)
在知道了电容和电感值之后,就可以求出谐振点频率,在此频率之前为容性,在此频率点之后为感性,下图的相位就说明了这一点;
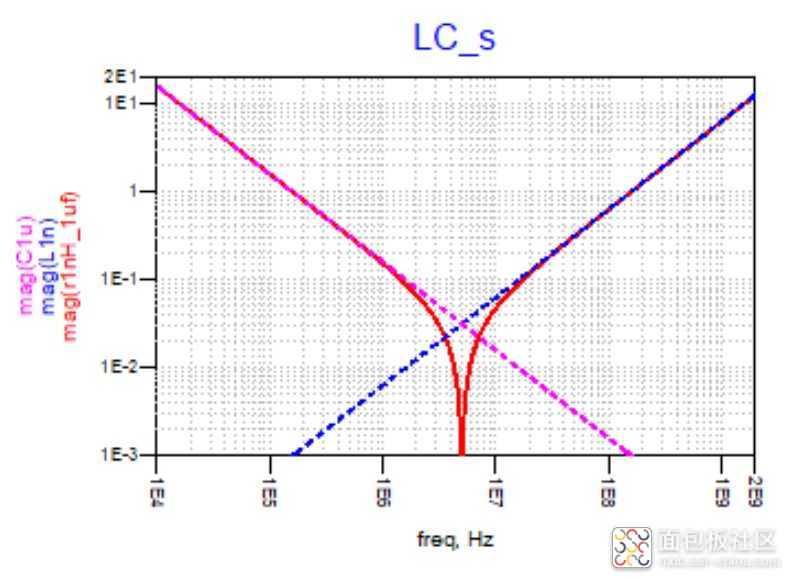
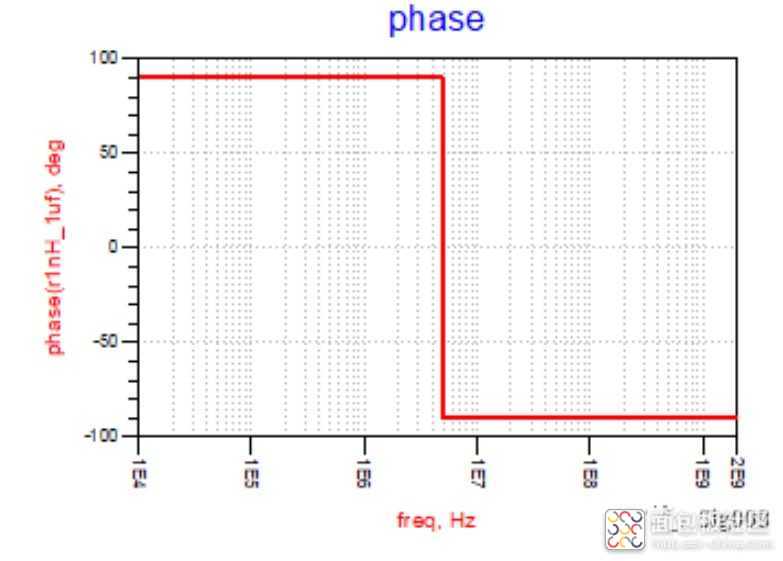
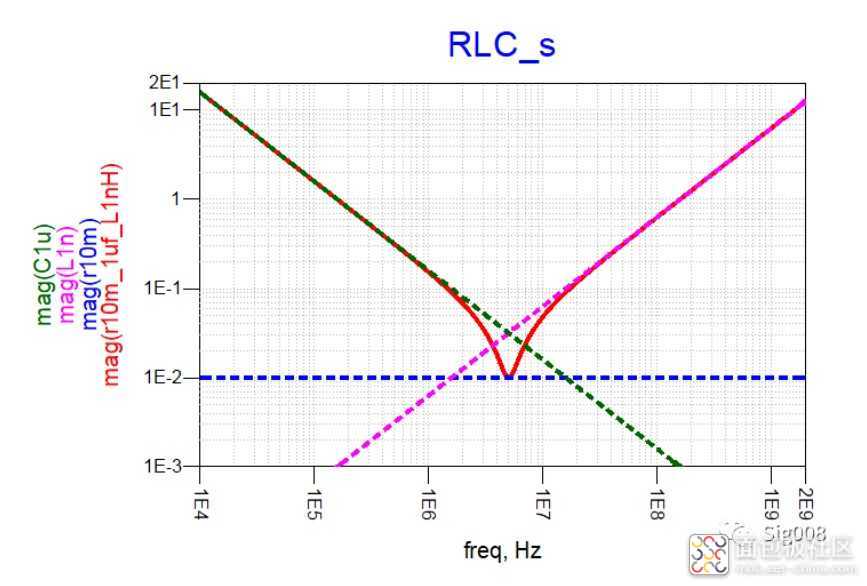
好了,以上这些是基本功,都是为了更好地了解非理想电容的阻抗特性做准备,下面请看真实电容的阻抗特性,即RLC串联(简单模型)
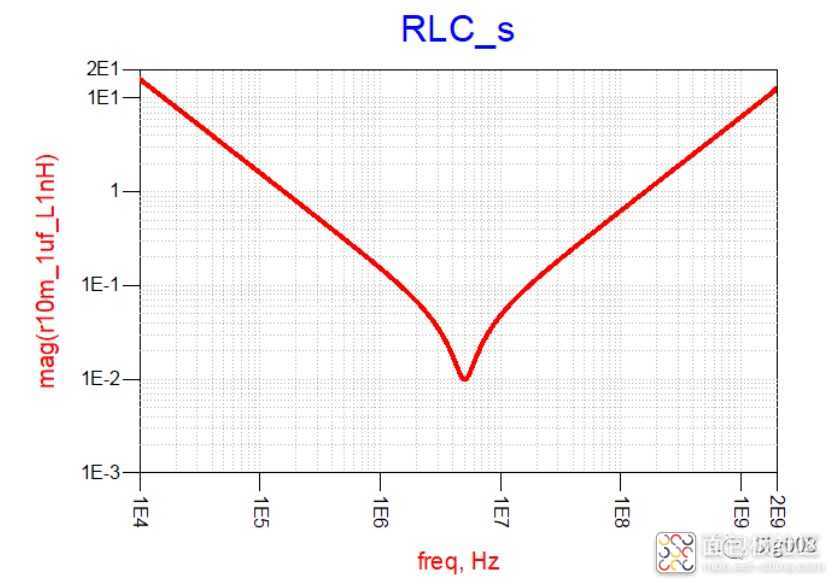
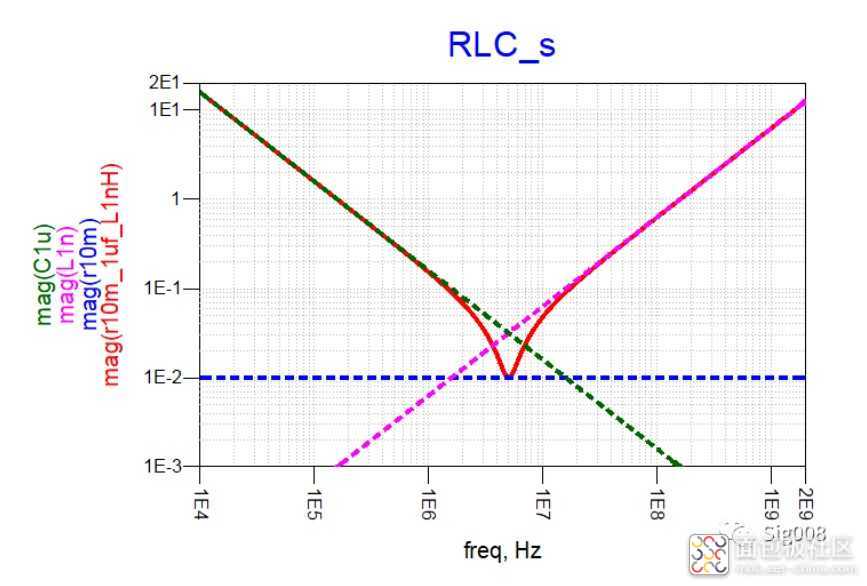
RLC串联后的曲线和LC比较像,同样是有一个自谐振频点,计算方法相同,在自谐振频点以前呈现容性,在自谐振频点以后呈现感性,LC之间也同样存在谐振,不同的是,此时的谐振大小是受控的,大小等于等效串联电阻的大小;
这就是非理想电容的阻抗特性,一定要印在大脑中,正是因为电容对高频的低阻抗特性,我们选择电容来降低PDN阻抗,但也因为电容的寄生参数导致的在某一频段后呈现为感性,因此要选取自谐振频点合适的电容,下面对比几个非理想电容的阻抗曲线,曲线来自电容厂家官方网站spice模型:
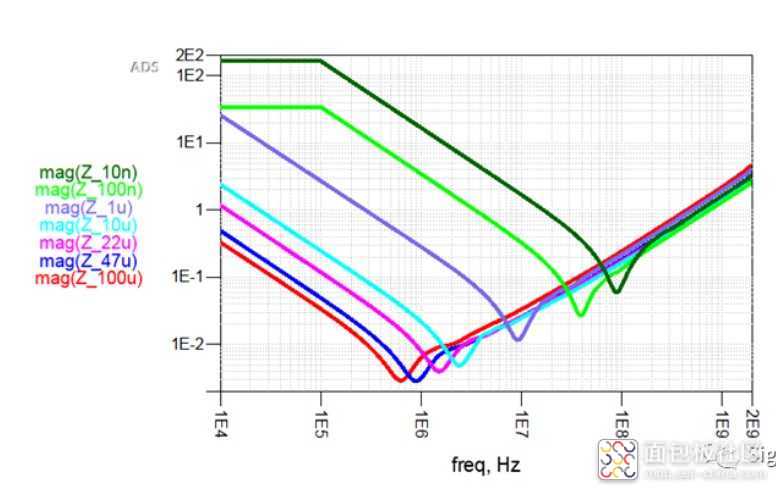
上边就是几组不同容值的电容阻抗曲线,从10nF到100uF,可以看到,在这个范围内(都是贴片陶瓷电容)寄生电感基本是差不多的,而由于电容容值的不同,导致各自的自谐振频点不同,因此在PDN中去耦时,就要选择合适的电容;
那么电容除了自身的自谐振频点以外,不同的电容在并联使用时还会出现反谐振频点,下篇文章就对相同容值电容并联、不同容值并联这两种情况来看电容并联的阻抗特性,这一特性在电容去耦时也会起到反作用,所以也是至关重要的一点。







 /4
/4 

