我是一直使用C语言写嵌入式程序的，最近看了一下STM32的触摸屏辅助工具touchGFX，其输出代码是C++，感受到了 C++在模块化代码生成中的优势。（我会陆续写一些关于 C++的文件，主要结合touchGFX工具，从嵌入式的角度看 C++的学习应用）。
元操作的由来
今天讲的元操作是基于类型的操作运算，而不是基于数值的运算，这点和普通程序代码有很大不同。问题起始于1994年，Erwin Unruh在一次C++会议上展示了一段不能编译的程序代码，这可能是最著名的一段无法编译的Erwin Unruh代码。
C++
  • template <int i> struct D
  • { D(void*); operator int(); };
  • template <int p, int i> struct is_prime {enum { prim = (p%i) && is_prime<(i > 2 ? p : 0), i -1> :: prim };
  • };
  • template < int i > struct Prime_print {
  • Prime_print<i-1> a;
  • enum { prim = is_prime<i, i-1>::prim };
  • void f() { D<i> d = prim; }
  • };
  • struct is_prime<0,0> { enum {prim=1}; };
  • struct is_prime<0,1> { enum {prim=1}; };
  • struct Prime_print<2> { enum {prim = 1}; void f() { D<2> d = prim; } };
  • #ifndef LAST#define LAST 10#endif
  • main () {
  • Prime_print<LAST> a;
  • }
    • 复制代码
    Erwin Unruh使用元操作编译器，但是显示这是无效 C++代码。为什么这段代码如此著名，请看下面的编译结果。
    forum.jpg
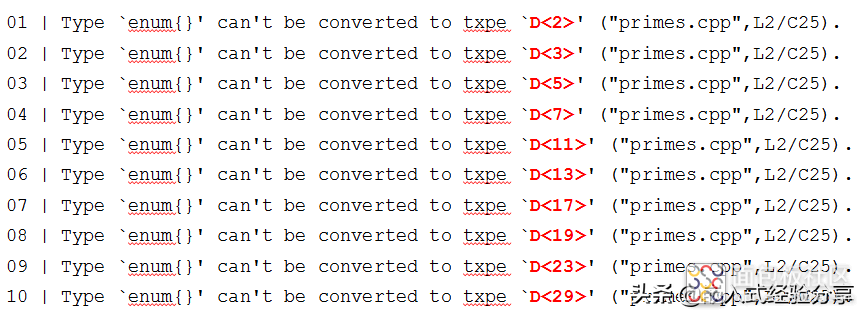
    编译结果
    请注意红色部分代码结构。 该程序在编译的过程中，计算出了前30个质数。这意味着模版实例可以在编译过程中完成计算，而且模版元操作是Turing-complete的（即状态自动转换），因此可以用于解决计算问题（当然，这里也要考虑到递归计算的深度问题，在C++11里至少可达到1024次递归计算）。
    元操作工作原理
    我们看一段阶乘的运算代码
    C++
  • #include <iostream>template <int N> // (2)struct Factorial{static int const value = N * Factorial<N-1>::value;
  • };
  • template <> // (3)struct Factorial<1>{static int const value = 1;
  • };
  • int main(){
  • std::cout << std::endl;
  • std::cout << "Factorial<5>::value: " << Factorial<5>::value << std::endl; // (1)std::cout << "Factorial<10>::value: " << Factorial<10>::value << std::endl;
  • std::cout << std::endl;
  • }
    • 复制代码
    在（1）处调用 factorial<5>::value实现了对 (2)处模版的实例化，在初始化的过程中Factorial<4>::value也被实例化。这种递归一直运算直到 template Factorial<1> ，满足 (3)处条件结束，看下图
    forum.jpg
    递归过程
    程序输出结果
    forum.jpg
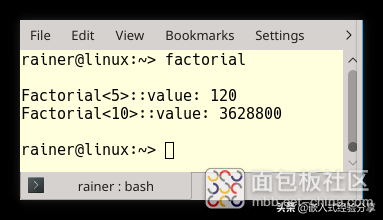
    结果
    那如何看到这结果是编译时运算的呢？
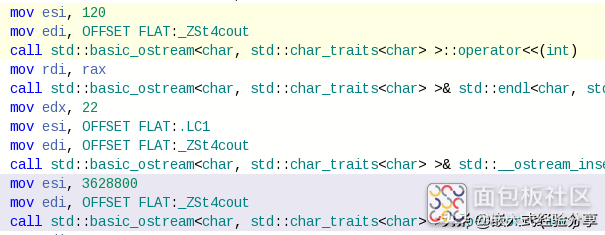
    forum.jpg

    forum.jpg
    上图加深语句的反汇编代码
    可以看到，factorial<10>直接就是一个常数3628800赋值，因此可判断是在编译过程中计算出来的。
    元操作虽然可以极大的提高程序运算效率，但是不建议大量使用，在嵌入式系统中适当的使用，却能极大的提高系统运行效率。在touchGFX里，使用到了typelist和元件操作，但是不是C++的库文件，是touchGFX里自定义的库文件，可以进一步提高效率，缩减代码。