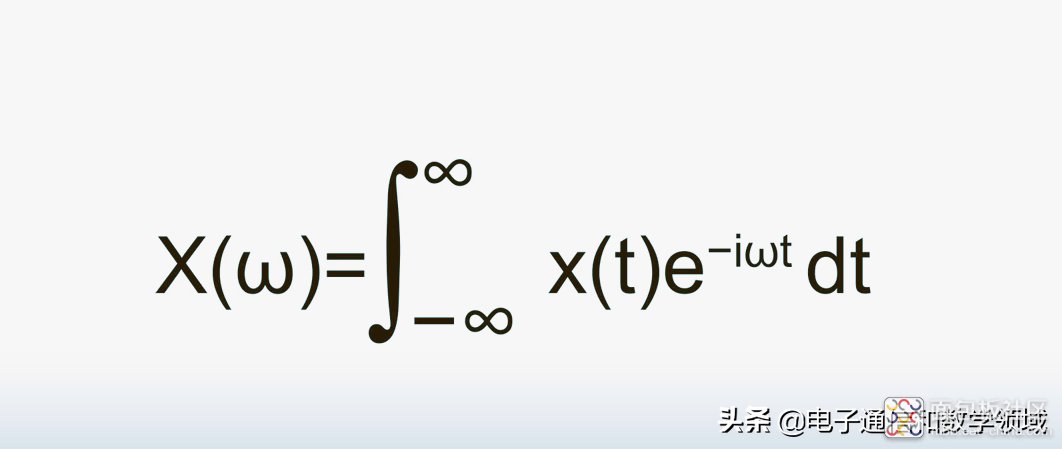
我们输入一个有关时间t的函数,就会得到一个有关ω的输出函数,这个公式会告诉我们信号中存在哪些正弦波。为什么这么说呢?
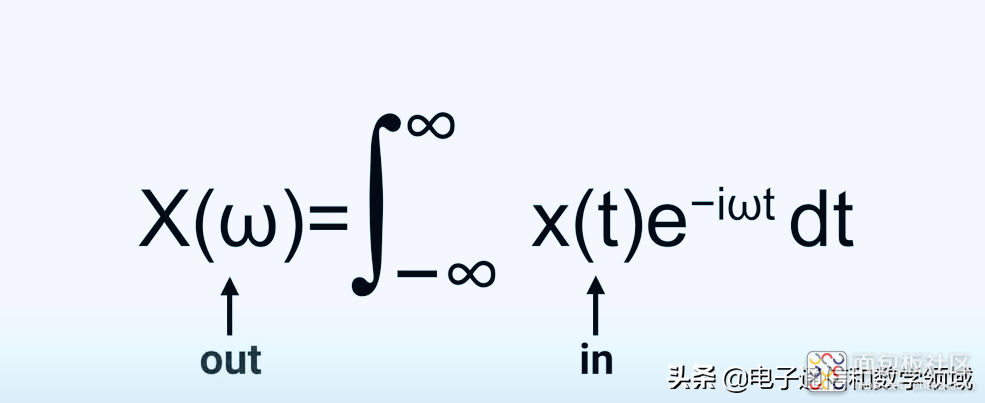
如果我们输入一个纯余弦函数或纯正弦波函数,输出函数只有一个尖峰,因为余弦函数是关于y轴对称的,所以你会看到两个尖峰,如下图所示
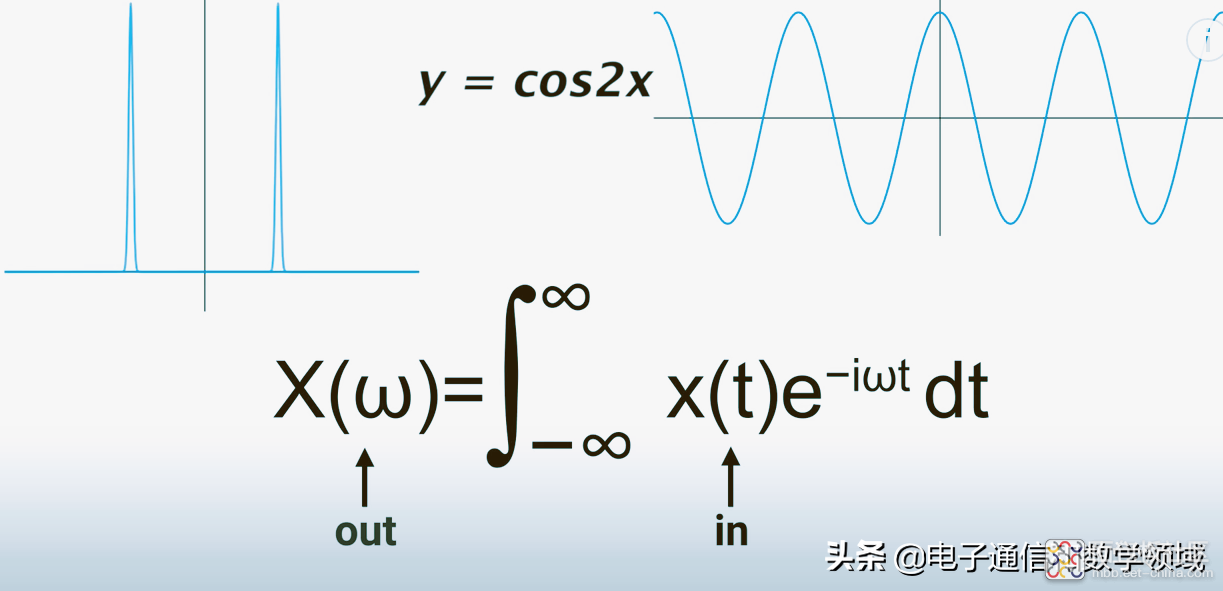
而且这两个尖峰对应的角频率ω=2和ω=-2
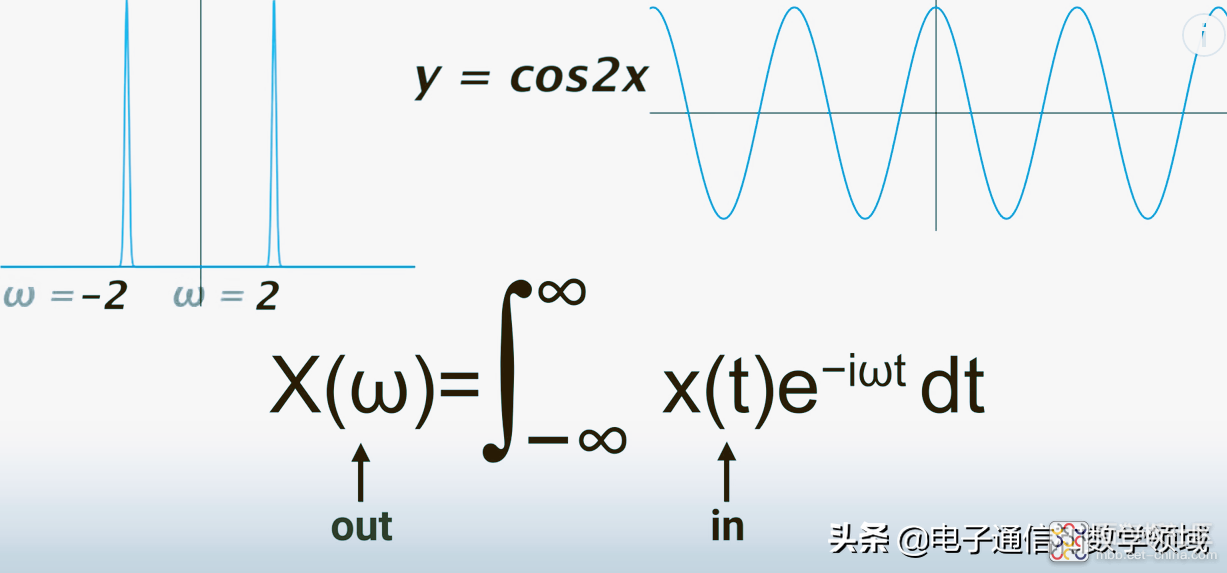
如果我们输入的是一个非周期函数,经过傅里叶变换就会得到一个更为复杂的结果,因为这个非周期函数需要无穷多个正弦波的叠加才能形成
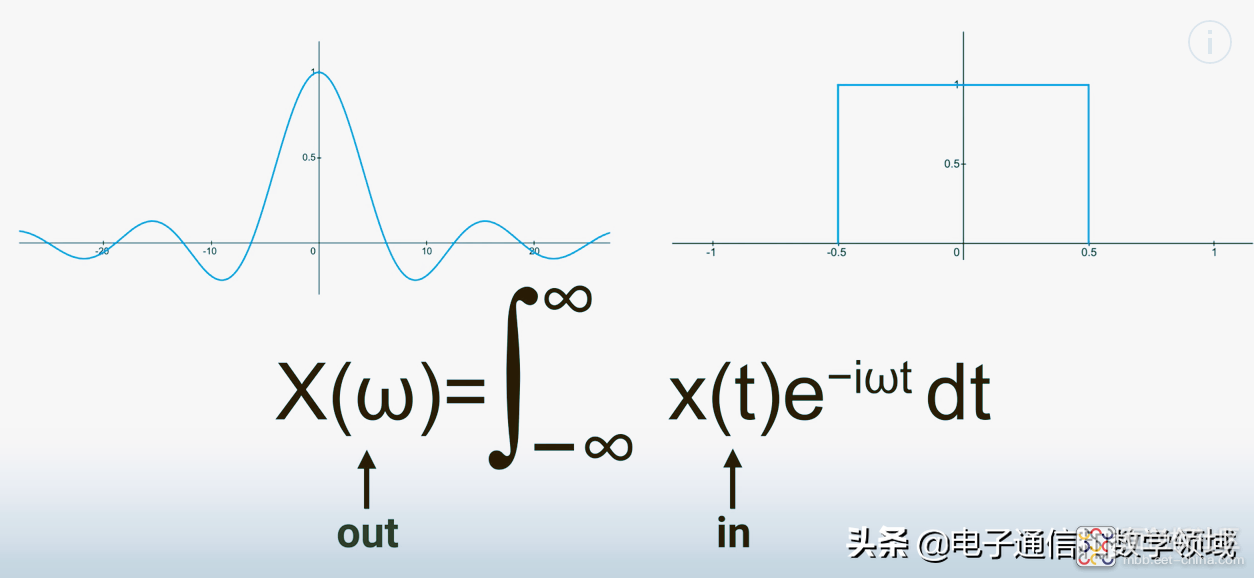
如下图所示:中间的蓝色部分,是无穷多个正弦波的叠加,构成了非周期的方波。右边的波浪线是f(t)在各个频率上的分布强度,可以理解为正弦波的强度
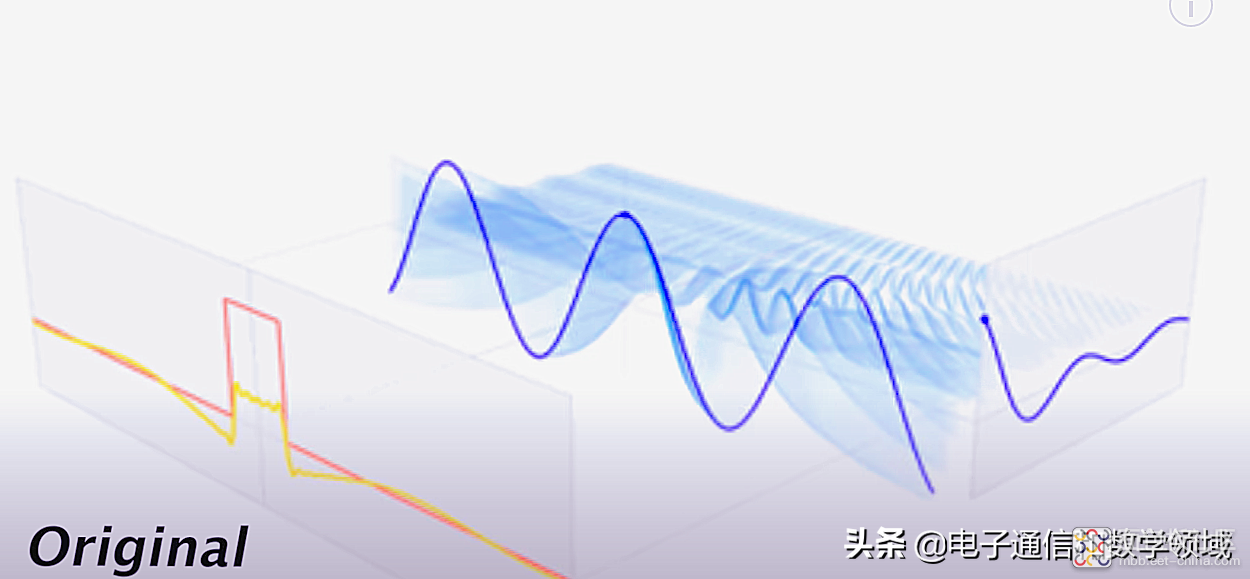


在这里有一个非常有意思的结论:傅里叶变换的零点,表示的是原始信号曲线下的面积,
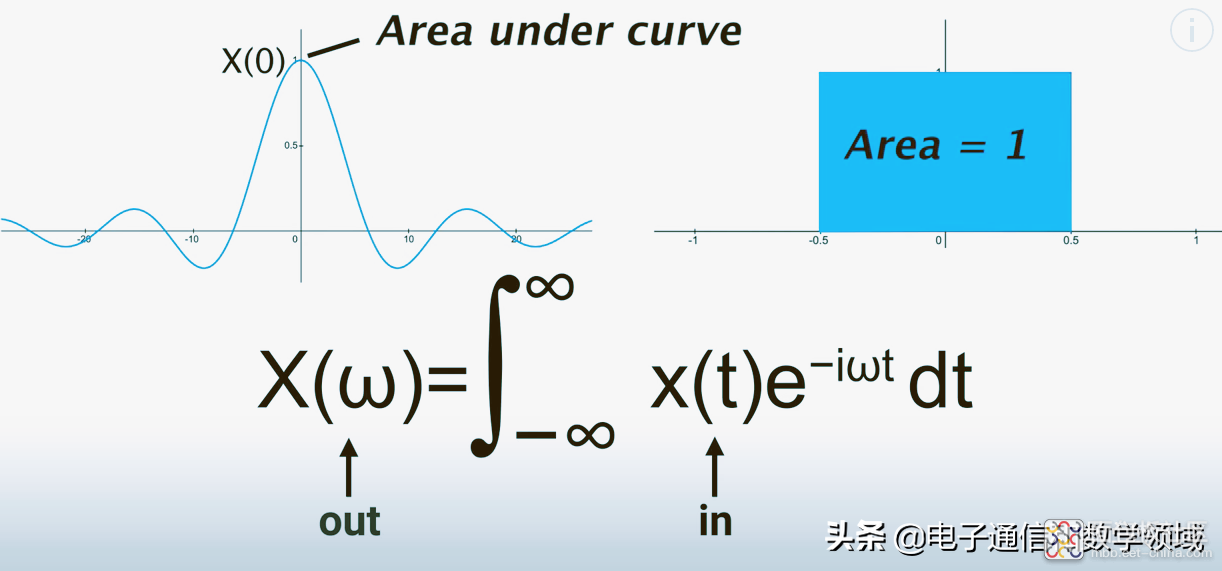
在这里,当角频率ω=0的时候,变换公式中有关e的指数项等于1
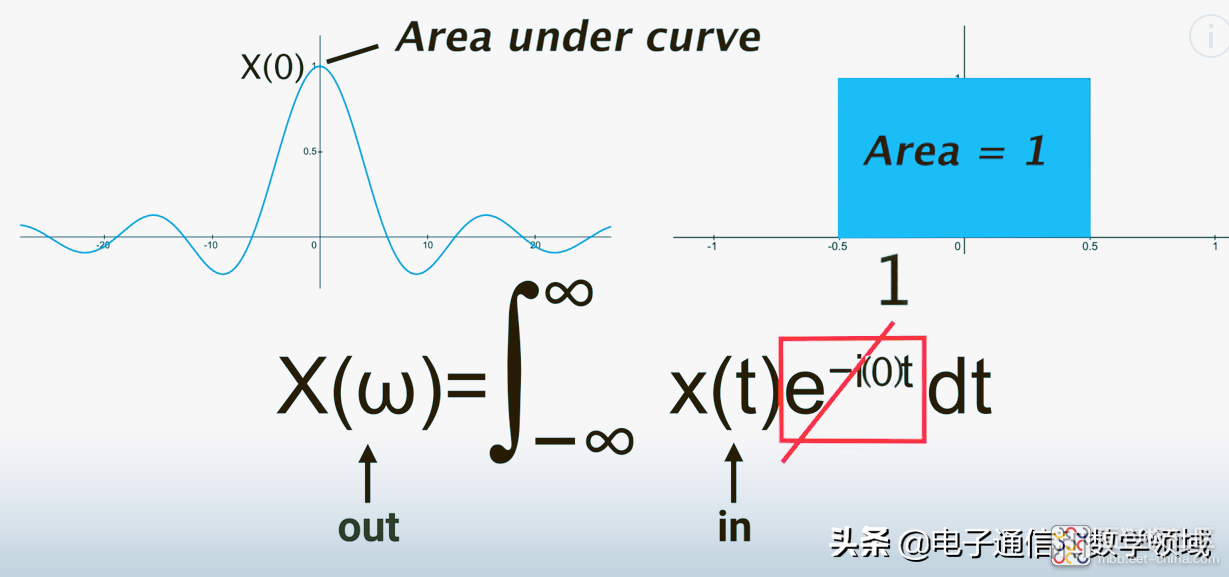
所以我们就得到了一个一般性的积分公式,它就是曲线下的面积,如下图所示
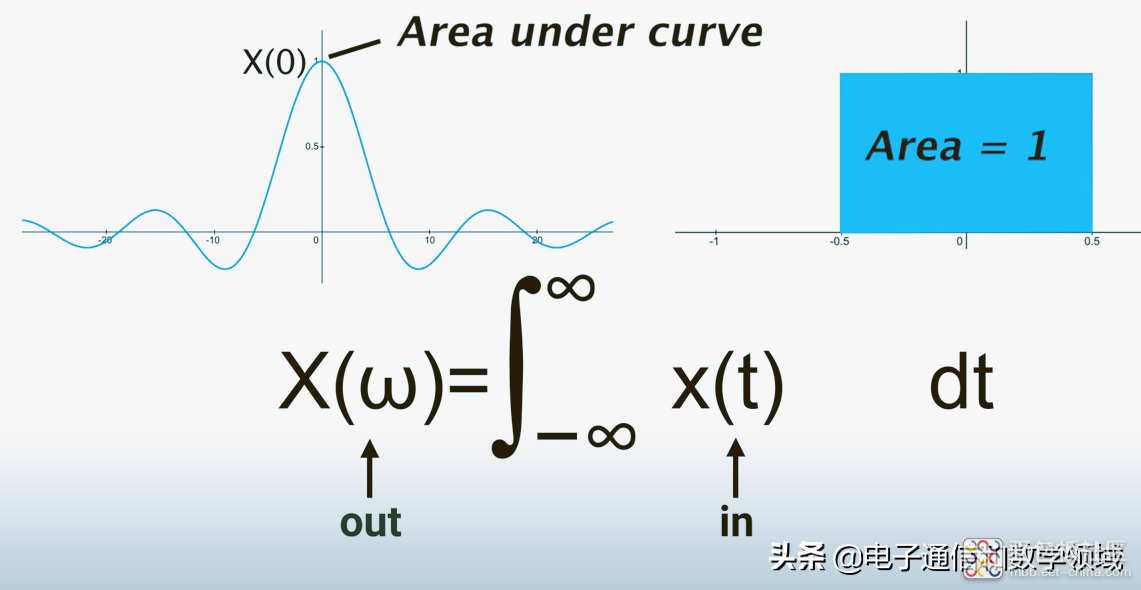
用图解的方法解读傅里叶变换的本质原理
傅里叶变换为非周期函数的处理提供了强有力的数学工具,我们用欧拉公式将e的指数项分解为实数和虚数两部分

我们以矩形函数为例,这个矩形函数的T=∞,左边对应的是实数情况下的余弦波,右边对应的是复数情况下的正弦波函数,我们来看这个波形是如何与傅里叶变换对应的
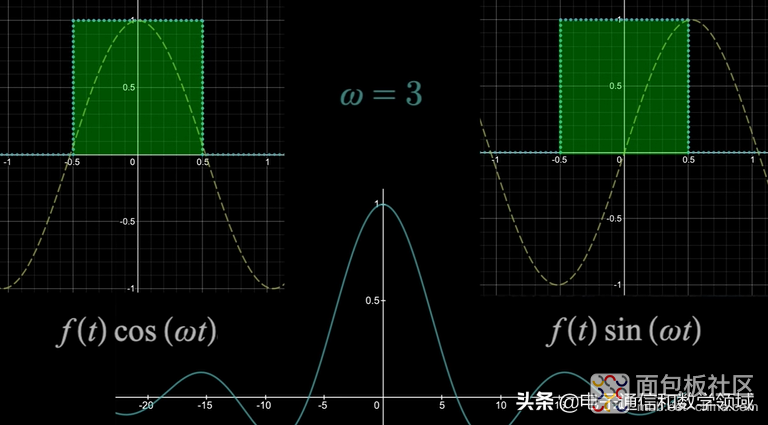
因为矩形波在-0.5<t<0.5的情况下等于1,其余都等于0,所以就是如下的图形
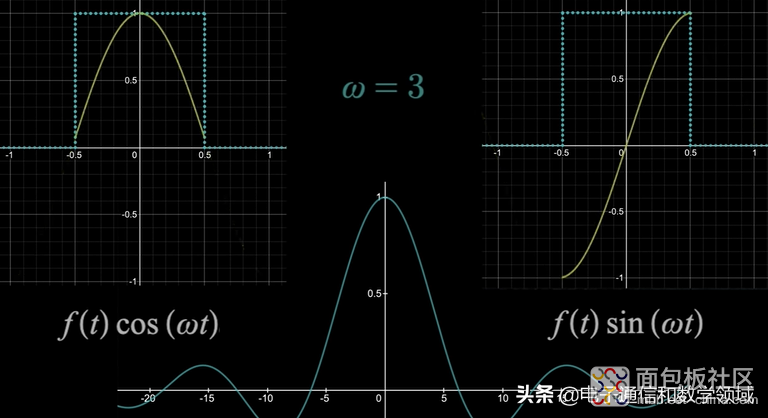
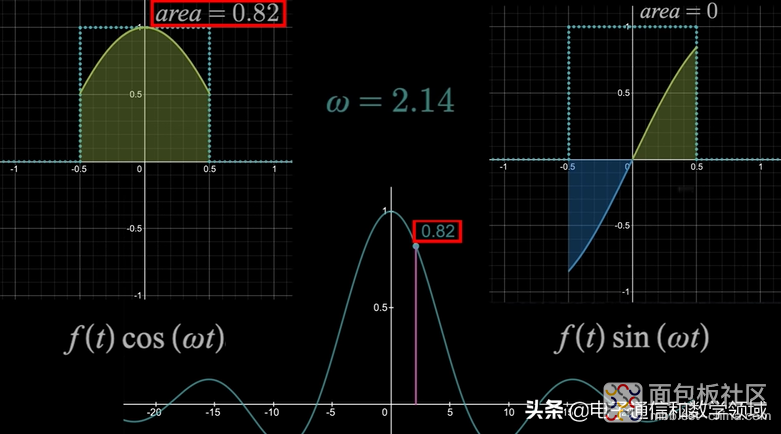
正余弦阴影区域的面积之和就是我们要得到的傅里叶变换
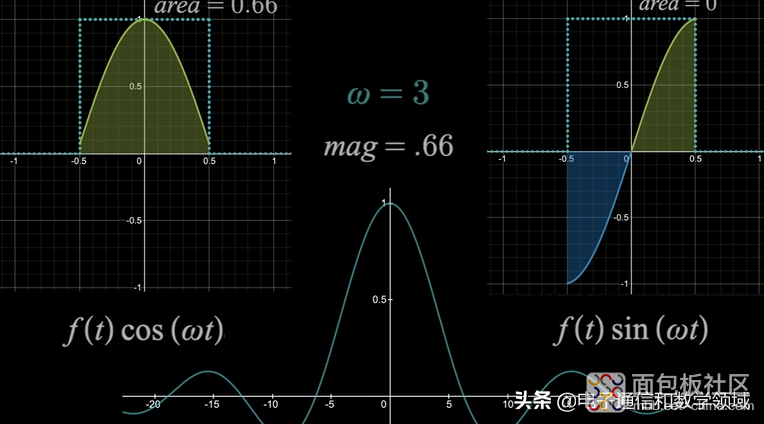
如下,当角频率ω=2.14时,左边图形下的面积=0.82,右边等于0,所以ω=2.14时傅里叶变换就等于0.82
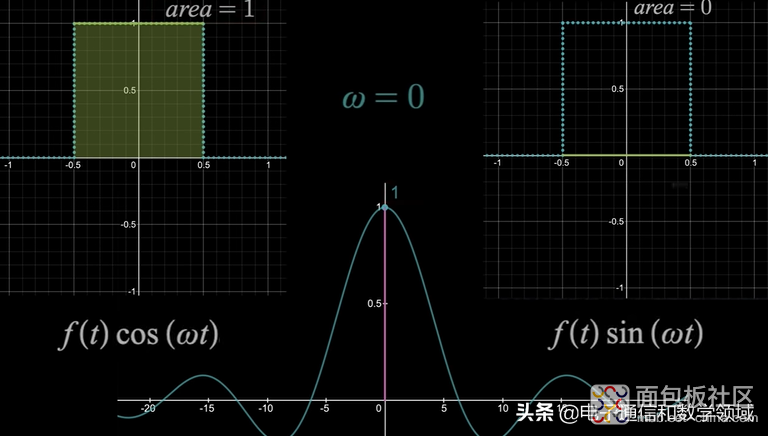
但有一个有趣的结论:ω=0时,傅里叶变换的值就是原函数曲线下的面积,如下图面积等于1,但右边的波形区域下的面积始终等于0
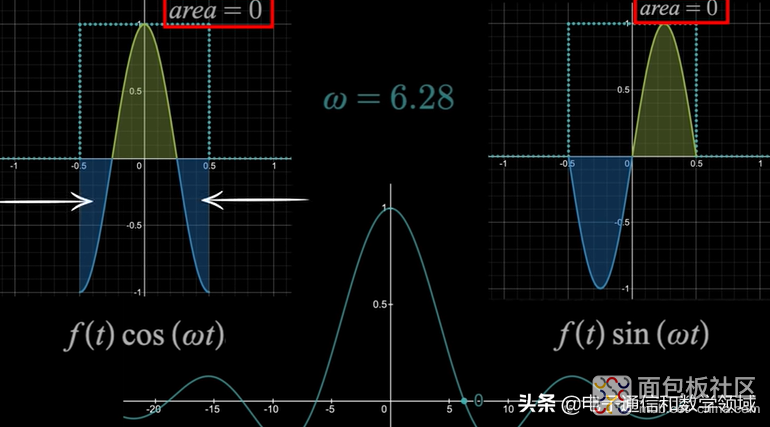
我们继续,当ω=6.28=2π时,左边的余弦波图形是一个完整的周期函数,所以面积等于0,右边的正弦波函数图形仍然等于0
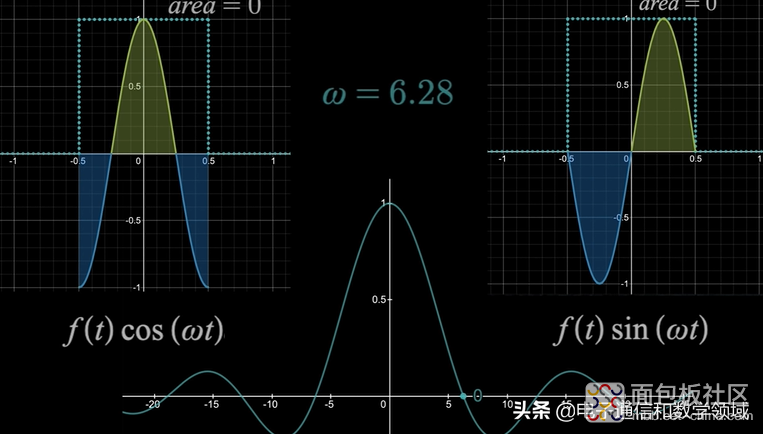
所以ω=0时,傅里叶变换F(ω)的值等于0
当ω=10.8,左边正弦波下的面积是-0.14,所以F(ω)=-0.14
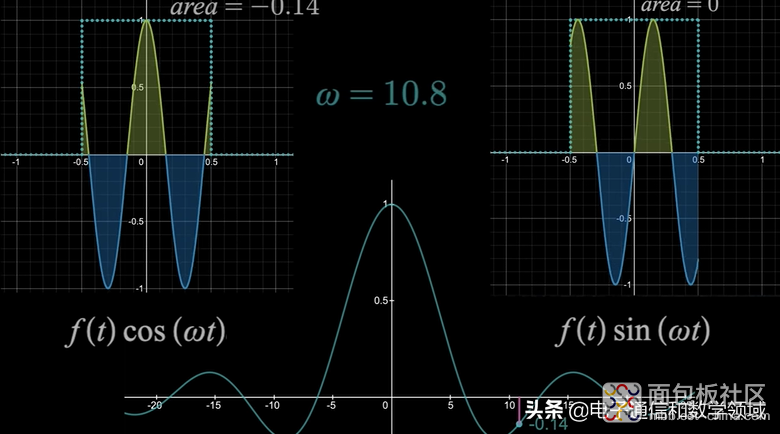
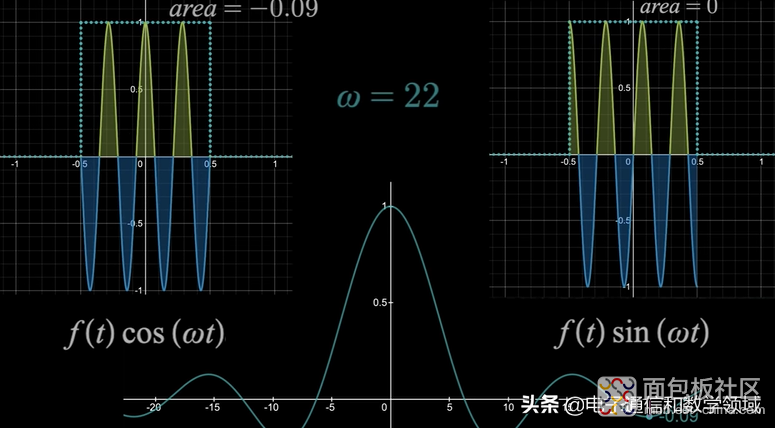
当ω=22时,左边正弦波下的面积是-0.09,右边图形下的面积始终等于0,所以F(ω)=--0.09,
方波的傅里叶级数和信号中的吉布斯现象
我们现在来确定如下图波形的傅立叶级数。来获得它振幅和相位谱。下图是一个周期性的方波
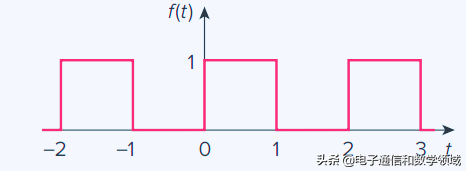
我们的目标是得到傅里叶系数a0 an和bn,首先,我们将波形描述为
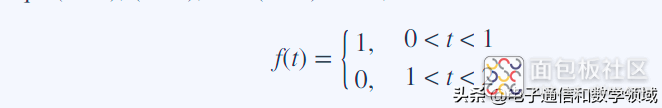
图中可知f (t) = f (t + t),因为t = 2,ω0 = = 2π∕t =π。因此,
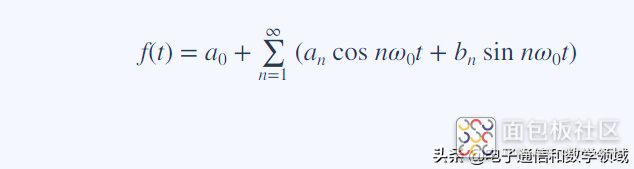
首先我们确定a0的值等于
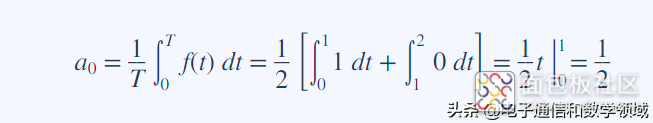
接着又可以确定an的值,这些都可以根据傅里叶级数原理公式得到,你会发现an=0
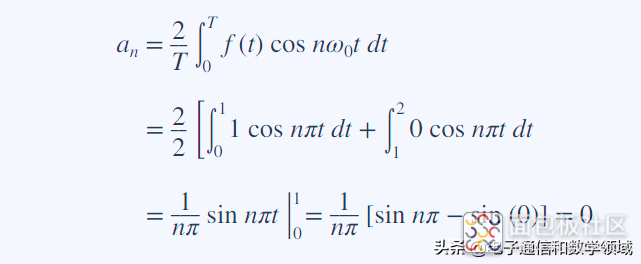
接着确定bn的系数等于
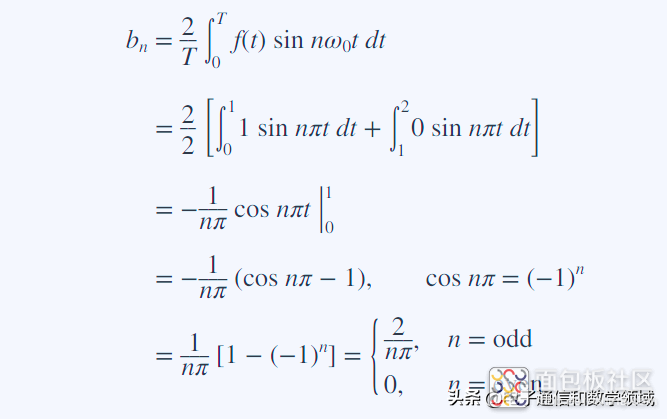
所以我们得到方波的傅里叶级数形式
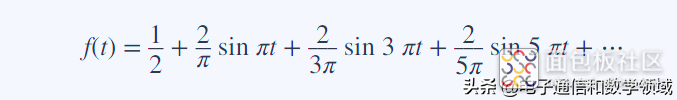
将各项逐一相加,随着越来越多的分量相加,和就变成了越来越接近方波。
。
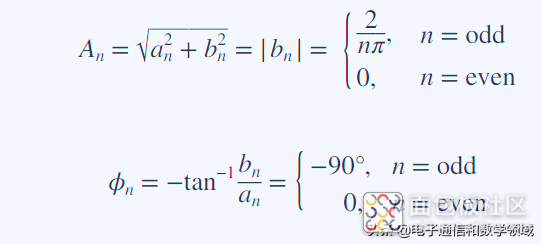
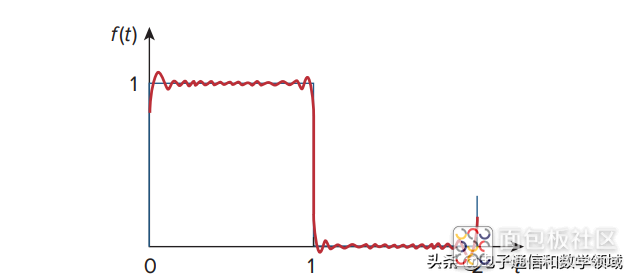
我们注意到部分和f(t)在不连续点的邻域上下振荡,(x = 0,1,2,…)时,存在振动和阻尼振荡。
在第一幕中,an无论用于近似f(t)的项的数量如何,总是会出现峰值约9%的超调。这叫做吉布斯现象。
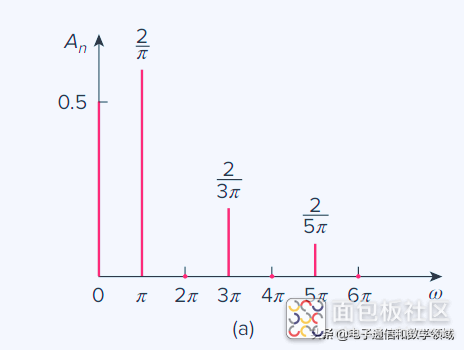
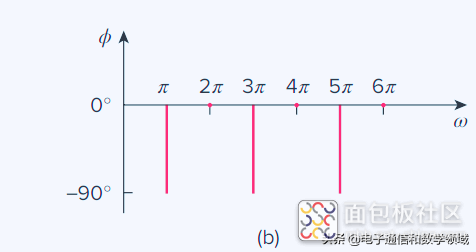
最后,我们得到了信号的振幅和相位谱
来源:电子通信和数学领域







 /2
/2 

