从数学原理上来说,通用型有源滤波器可以用如下的系统框图来表示。
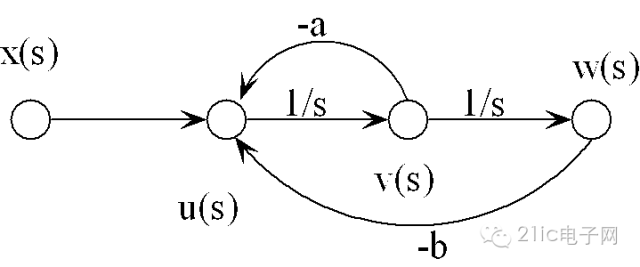
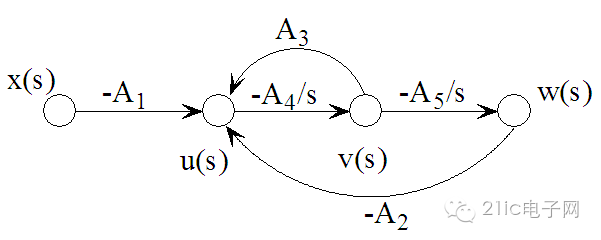
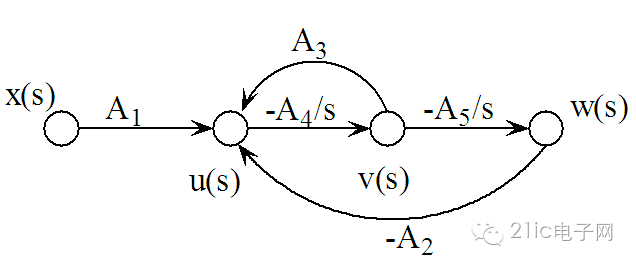
图 1 典型的二阶系统的信号流图
上面是一个典型的二阶系统的信号流图,利用Mason 公式可以很容易的得到系统各个通路的传递函数:
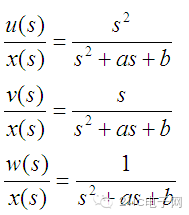
上面三个式子分别对应高通、带通和低通滤波器,如果将u、v、w三路信号加权叠加则可以组成任意的二阶系统。
二阶系统传递函数的分母多项式的标准形式为:
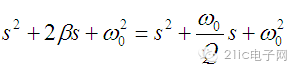
经比较可知,大环路增益b决定二阶系统的固有频率,小环路的增益a决定系统的阻尼系数,也就是决定系统的品质因数Q。
状态变量滤波器
状态变量滤波器也被称为KHN 滤波器,属于通用型有源滤波器的一种实现形式,由Kerwin、Huelsman’Newcomb与1967年提出的。电路的基本形式如下。
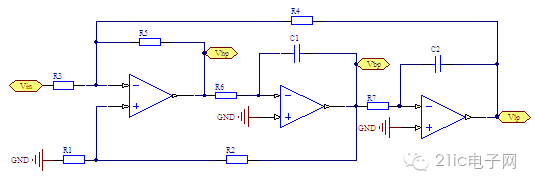
图 2 反向输入型KHN 滤波器
转换为信号流图后如下图所示。
其中:

列写系统各个通路的传递函数如下:
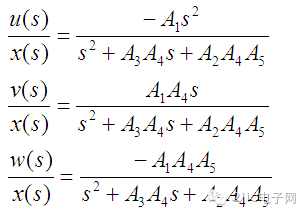
将(3)带入(4)后经整理可得:

如果对电阻电容的值做一些限制,公式会变得更简单。设:
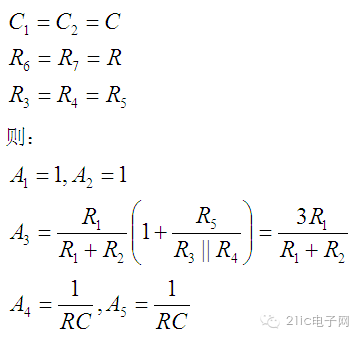
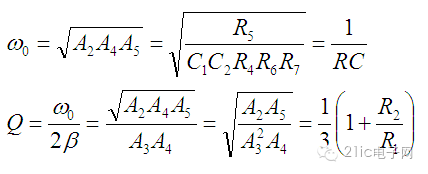
可以看出品质因数Q只依赖于R1与R2的比值。而固有频率只与RC的乘积有关。
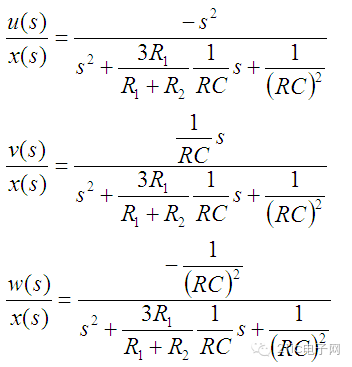
正向输入型的KHN滤波器如下图所示:
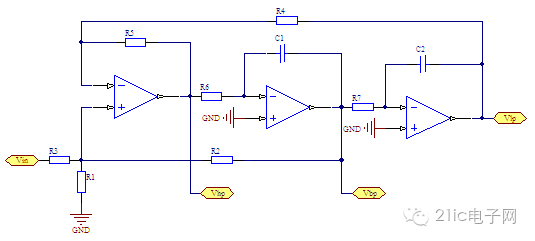
图 3 正向输入型的KHN滤波器
对应的信号流图如下:
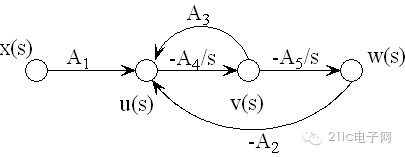
从信号流图上看,仅仅是x(s) 到 u(s) 之间的增益从 -A1 变为 A1,其他的地方完全相同。但是由于R3从运放的负输入端移动到了正输入端,所以A1和A3的值发生了很大的变化。
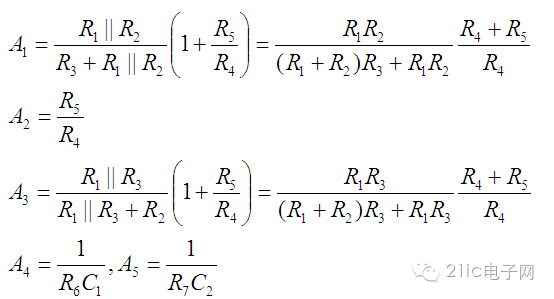
列写系统各个通路的传递函数如下:
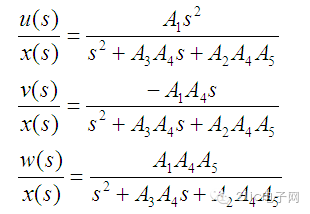
由于A2、A4和A5都没有变化,所以系统的固有频率没有变:

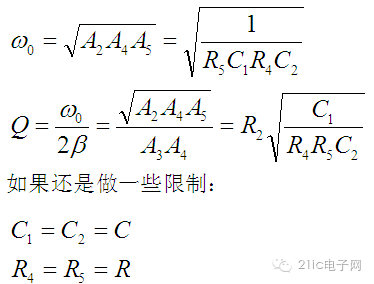
如果还是做一些限制:

则可以简化为:
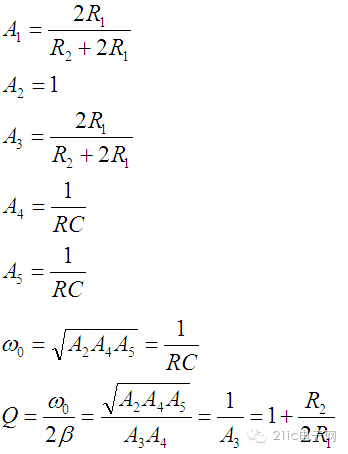
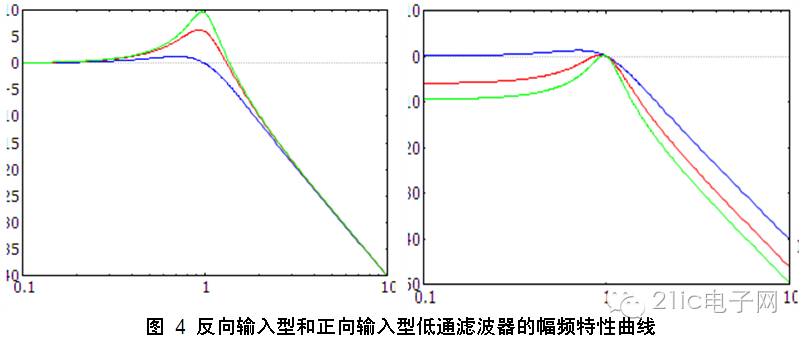
正向输入型和反向输入型最大的区别在于通频带的增益。下面给出低通滤波器时的幅频特性曲线。两边的曲线一对比他们的区别就一目了然了。
Tow-Thomas 型二阶滤波器
另一种类似的电路形式称之为 Tow-Thomas 型滤波器。它的基本电路形式如下,其中R3=R6构成一个反向器。
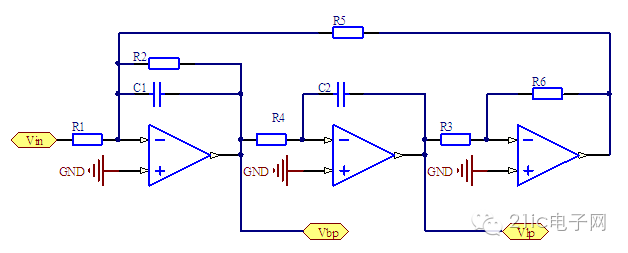
图 5 Tow-Thomas 型滤波器
信号流图与正向输入型KHN滤波器完全相同。需要说明的是u(s)是电流信号,表示的是流过C1的电流的大小。
但是A1到A5的表达式却变得简单的多。
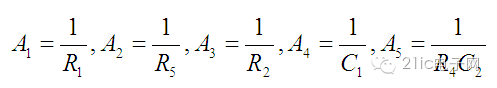
列写系统各个通路的传递函数也与正向输入型KHN滤波器完全相同,这里重复如下:
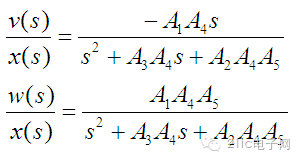
由于u(s)是电流信号,无法直接引出使用,因此也就没有列出来。将(16)带入(17)后可得:
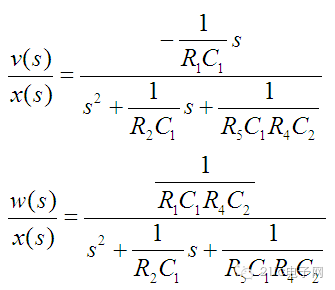
品质因数和固有频率计算如下:
则可以化简为:
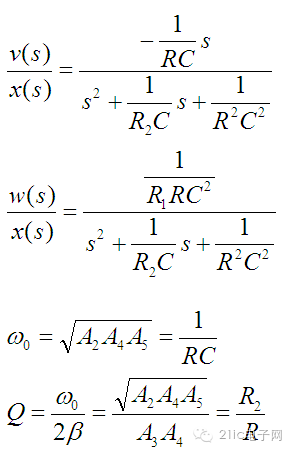
原始信号减去带通信号就称为带阻信号了,因此再增加一个运放就可以实现带阻型滤波器。
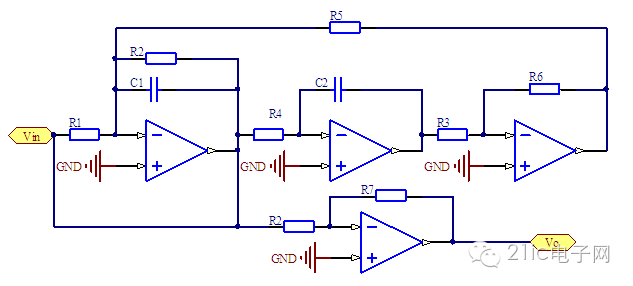
图 6 Tow-Thomas 带阻型滤波器
这个电路的要点是R1=R2,这样才能保证原始信号与带通信号的幅度相同。也就是说要求A1=A3。
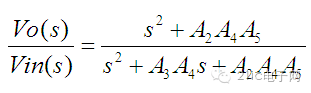
简单的说,这种办法生成的带阻滤波器其实就是在虚轴上对应位置添加了零点。
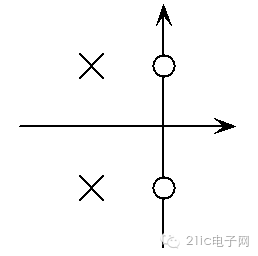
图 7 Tow-Thomas 带阻型滤波器的零、极点分布
带阻信号如果再与低通信号相加,就能够组成低通带阻型或高通带阻型。下面是电路原理图。
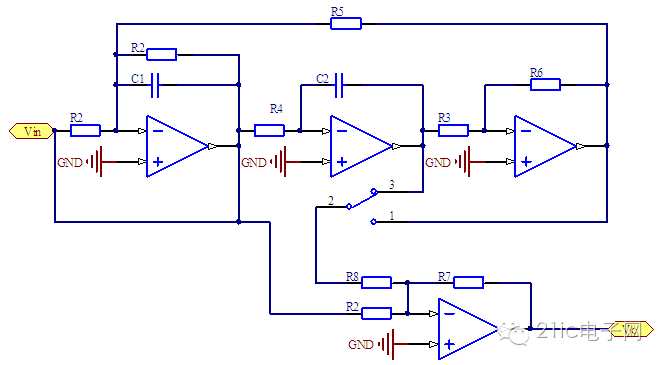
图 8Tow-Thomas (高通/低通)带阻型滤波器
单刀双掷开关打到3的位置时对应低通带阻滤波器,打到2的位置时对应高通带阻滤波器。原理可以这样分析。首先,传递函数可以写为如下形式:
单刀双掷开关打到3的位置时α的值为正,打到2的位置时α的值为负。α 值的变化对应的是系统零点的移动。α大于0 相当于零点互相远离。
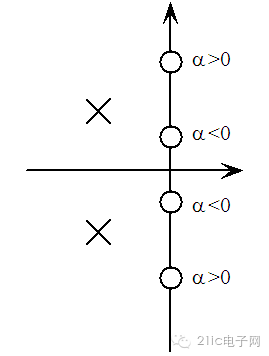
图 9 Tow-Thomas (高通/低通)带阻型滤波器的零、极点分布
(高通/低通)带阻型滤波器的典型频响如下面两幅图所示。
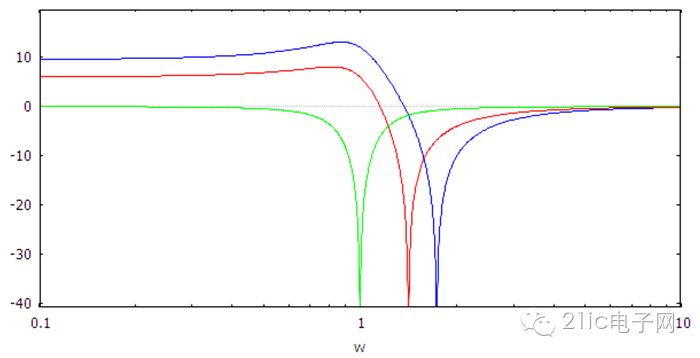
图 10 低通带阻型滤波器的幅频响应
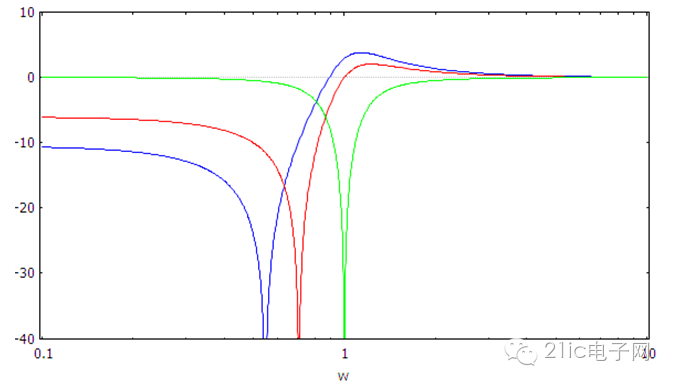
图 11 高通带阻型滤波器的幅频响应
来源:21ic








 /5
/5 


