MOS是金属氧化物半导体结构,氧化物是绝缘层,有绝缘层即意味着存在电容。大家知道,电容常见表达式为
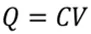
,即电容存储的电荷是电容与电压的乘积;
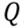
是电流与时间的积分,而MOS中的阈值电压
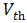
受到电容的控制,因此电容决定了MOS的开启速度,进而也就决定了IGBT的频率响应特性。
还是以沟槽型IGBT的MOS结构为例,如图所示,其输入电容包含两个部分,一是栅极与源极之间的电容
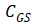
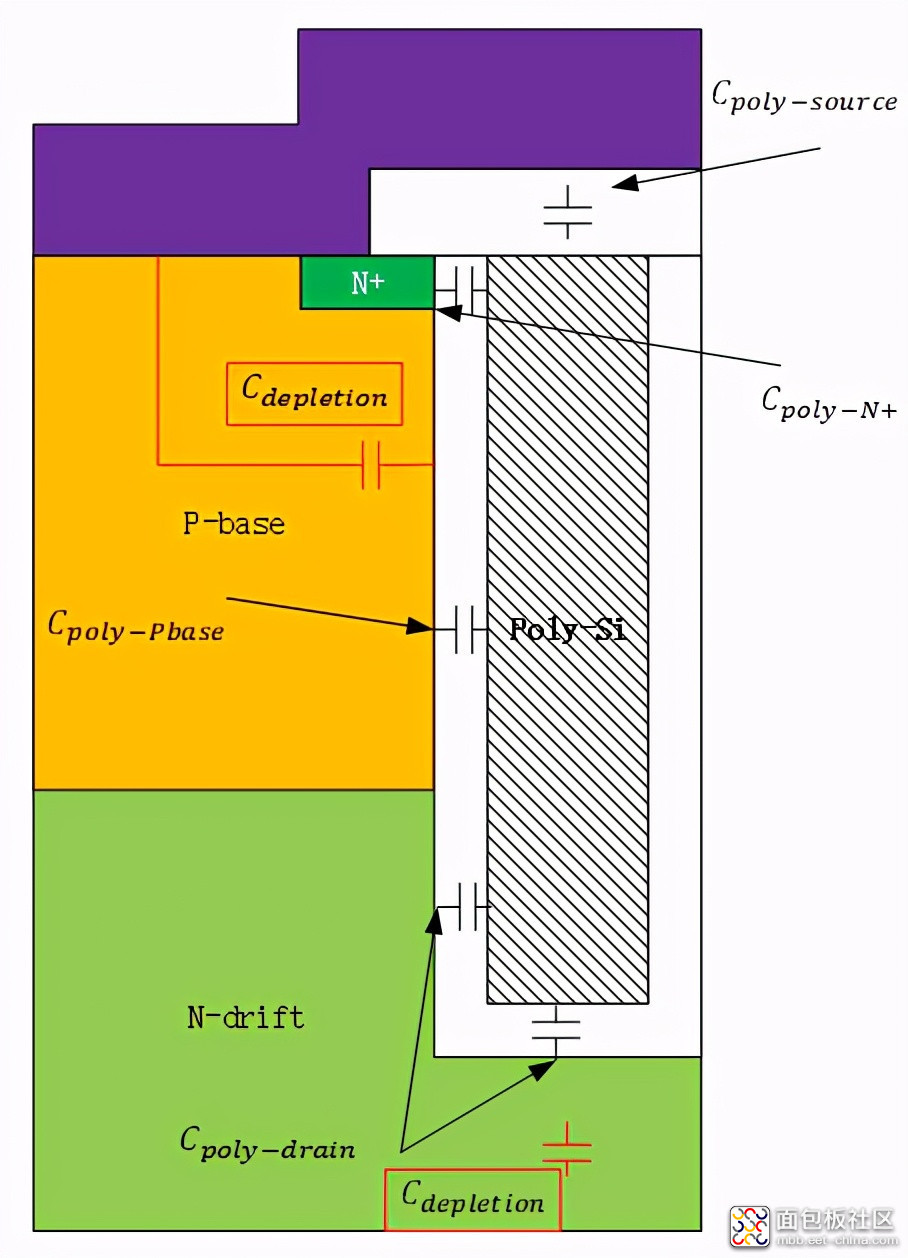
,二是栅极与漏极之间的电容
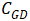
。
我们先看
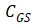
,包括(
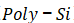
)与
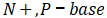
,以及金属的重叠部分,即栅极与源极之间的电容
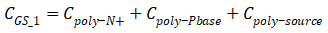
等式右边的各项电容均可根据其几何尺寸计算得出,
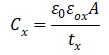
其中,
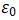
为真空介电常数,
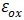
为氧化物的相对介电常数,
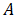
为重合面积(注意,这里忽略了重叠的边缘部分电容)。
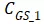
地下标加一个“1”,是因为这个表达式还需要修正。
回顾一下之前对于MOS能带弯曲的分析,随着栅极电压的增加(P型半导体),半导体与氧化硅界面会经历先耗尽后反型的的过程,最终形成沟道。所以
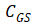
中还存在一个耗尽电容
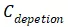
,与
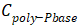
串联。
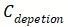
是一个随栅极电压变化的电容。当MOS栅极施加负电压时,栅氧与P型硅表面会产生积累的正电荷,相应地,在栅氧与多晶硅的界面产生负电荷积累,这是一个对
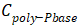
充电的过程,所以
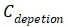
可认为不存在;当MOS栅极施加正电压时, P型硅表面的空穴被排斥,形成耗尽区,导带向接近费米能级的方向弯曲,耗尽区的宽度对应
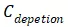
。在前面对MOS阈值电压的“强反型”说明中,未做具体推导,但给出了强反型的结论,即
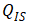
将随
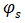
呈指数级增长,根据电容的定义,
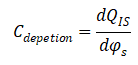
显然耗尽区的宽度会随栅极电压
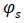
的增加而增加,直到反型层形成,耗尽区不再扩展,相应的
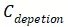
达到最小值。所以,可以预期
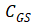
的变化趋势如下图所示。
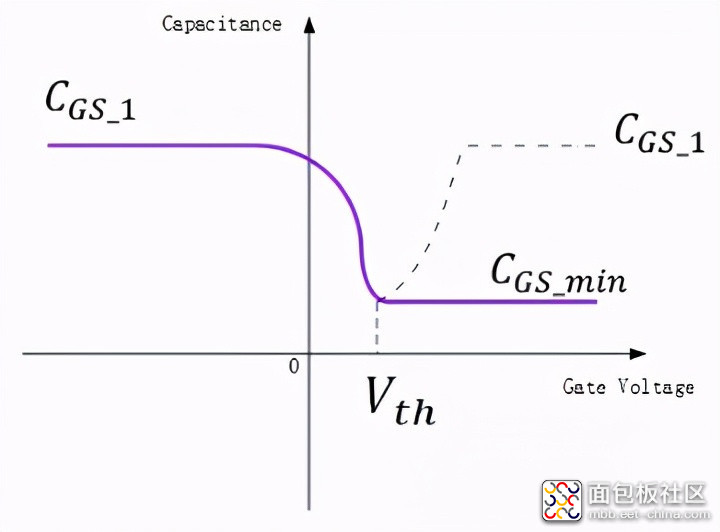
注:因为电容测试必须用交流信号,而反型层的电荷分布可能会随交流信号的变化而变化,尤其是对于功率MOS而言,反型层中电子很容易从发射极得到补充,所以
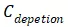
在低频信号下难以测到,经常测到的CV曲线是图中的虚线所示。
上一章我们讲到
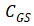
的变化趋势,至于
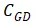
,可以按照相同的方式进行分析,即 栅极与漏极极之间的电容。开通过程中,因不存在耗尽反型过程,所以
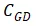
就是栅氧与N_drift区域重叠的部分所形成的电容;但是关断过程中,因为P-base和N_drift所形成的PN结承受高压而产生耗尽区,所以也会形成一个与
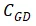
串联的耗尽区电容,如图中所示,这里不再详述。
至此,我们是不是可以得出输入电容就是
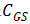
和
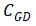
之和呢?还差一步,因为MOS使用过程中还存在负载,对输入电容是有影响的。根据前面对MOS的IV特性分析,可以将MOS视为一个电压控制型电流源,其共源极等效电路如下图。
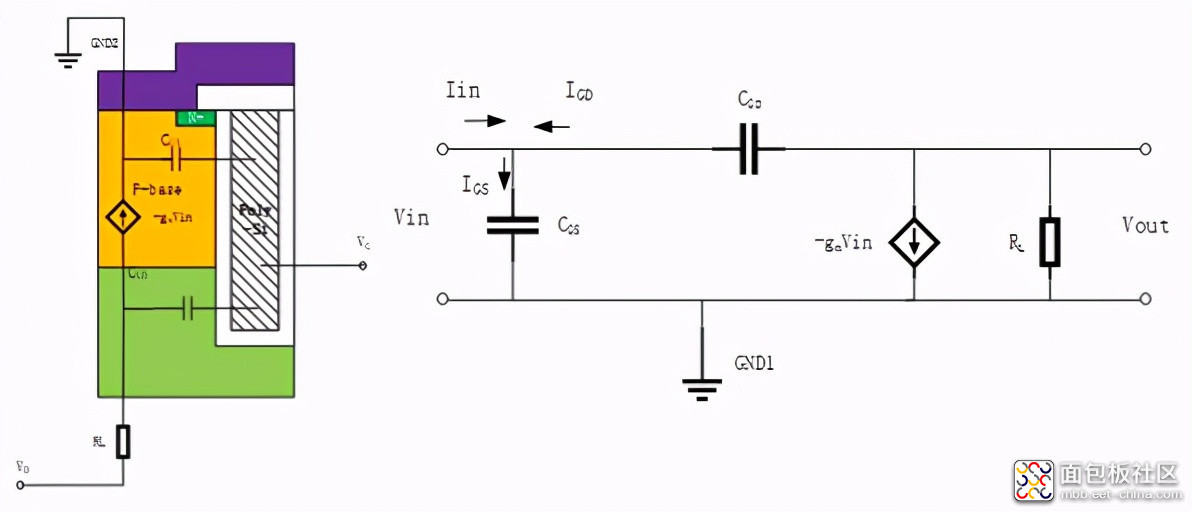
根据电路的基本原理,假设输入电容为
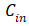
,那么
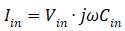
根据等效电路,
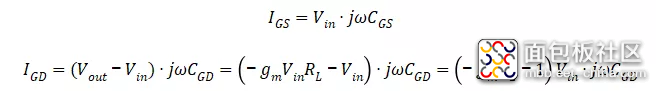
显然,
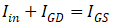
,综合以上几个关系式易得,
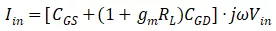
对照
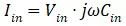
,得到MOS结构的输入电容为:
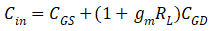
定义上式右边第二项为米勒电容,
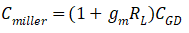
。显然米勒电容是随栅极电压变化的。
前面讲到MOS结构中电容的存在会决定器件的响应速度,即器件可工作的频率范围。从MOS的工作机制容易看出,开启过程中,电子从源极传输到漏极的时间主要由两个部分构成:
一是栅极电容的充电时间,至形成反型沟道,从而具备电子传输的通道;
二是电子从沟道中通过的时间,对于功率型MOS而言,还要包括电子通过低掺杂扩散区直到漏极的扩散时间。
对于关断过程,则与开启相反。这里我们把前者称为开关时间
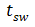
,后者称为渡越时间
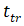
。
对于渡越时间
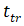
,这里将其物理过程描述如下,感兴趣的读者可以参考作推导。渡越沟道所需时间取决于沟道内的电子饱和速度和沟道长度,
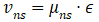
,即速度取决于沟道内的迁移率和沿沟道方向的电场强度,该电场强度又取决于漏极和源极之间的电势梯度
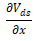
;渡越低掺杂扩散区所需时间取决于扩散速度和扩散区深度
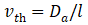
,即速度取决于与扩散系数和平均自由程,扩散系数同样与扩散区的迁移率相关,而平均自由程则与浓度相关。
下面对与电容充电相关的开关时间
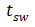
作简要分析。随着频率的增加,输入电容的容抗减小
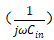
,所以频率响应一定存在一个极限值,这个极限值通常被定义为截止频率,对应输出电流与输入电流的增益为1时的频率。即:
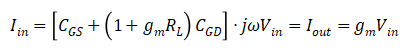
化简后,
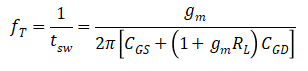
来源:网络







 /1
/1 

