 12.jpg1100x848 170 KB
12.jpg1100x848 170 KB 以下内容包括Part1~Part3三部分,帮你解决运算放大器带宽问题。
互阻抗放大器是一款通用运算放大器,其输出电压取决于输入电流和反馈电阻器:Part1
我经常见到图 1 所示的这款用来放大光电二极管输出电流的电路。几乎所有互阻抗放大器电路都需要一个与反馈电阻器并联的反馈电容器 (CF),用以补偿放大器反相节点的寄生电容,进而保持稳定性。
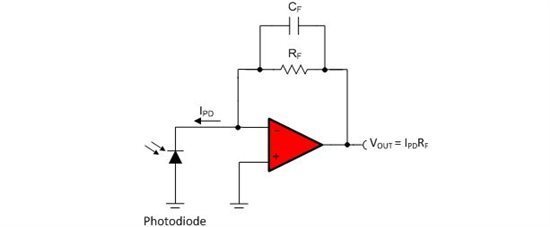
图 1:反馈电容器 CF 可补偿光电二极管接点电容及运算放大器输入电容
有大量文章都介绍了在使用某种运算放大器时应如何选择反馈电容器,但我认为这根本就是错误的方法。不管我们半导体制造商相信什么,工程师都不会先选择运算放大器,然后再通过它构建电路!大部分工程师都是先罗列一系列性能要求,再寻找能满足这些要求的部件。
鉴于这种考虑,最好先确定电路中允许的最大反馈电容器,然后选择一个具有足够增益带宽积 (GBW) 的运算放大器,以便能与该反馈电容器稳定工作。
下面是为互阻抗放大器确定所需运算放大器带宽的简易方法的步骤。
步骤 1:确定允许的最大反馈电容。反馈电容器连同反馈电阻器构成放大器频率响应中的一个极点:

高于这个极点频率时,电路的放大性就会降低。最大反馈电容器值可由反馈电阻器和所需的带宽确定:

我们可通过让反馈电容器等于或小于公式 3 计算得到的值,来确保电路满足带宽要求。
步骤 2:确定放大器反相输入端电容。在图 2 中,重画了图 1 的电路,以显示光电二极管的接点电容 (CJ) 以及放大器的差分 (CD) 及共模(CCM1、CCM2)输入电容。这些值通常在运算放大器和光电二极管的产品说明书中提供。
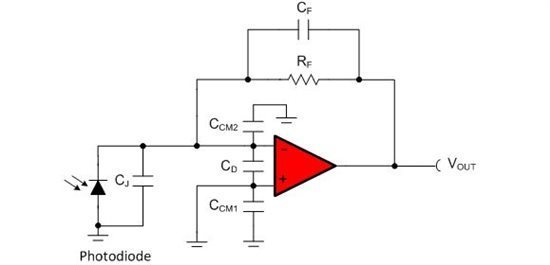
图 2:显示反相节点电容的互阻抗放大器电路
从本图中可以很明显看到 CJ、CD 和 CCM2 是并联的,因此反相输入端电容是:
由于非反相端接地,因此 CCM1 不会增加输入电容。这时候 CD 和 CCM2 可能还不知道,因为我们还没有选择特定的运算放大器。我经常将 10pF 作为其相加过后的合理估计值。随后可用确切值来替代,以确定特定运算放大器是否合适。
既然我们已经确定了 CF 和 CIN 的值,那现在就能计算出所需的运算放大器带宽。我将在第二部分介绍该计算,并在设计实例中应用以上过程。
在Part1中,我介绍了互阻抗放大器所需运算放大器带宽的三步计算过程中的前两步。在本文中,我不仅将介绍最后一个步骤,而且还将介绍使用本计算过程的设计实例。Part2
步骤 3:计算所需运算放大器增益带宽积
进行基本稳定性分析,我们将获得本步骤背后的逻辑,如果您只想进行计算,可以直接跳到公式 5。图 1 是用于分析的 TINA-TI™ 电路。反馈环路使用大电感器 (L1) 中断,而电压源则可通过大电容器 (C1) AC 耦合至该环路。该环路在运算放大器输出端中断,以便输入电容的效果包含在分析中。我们可执行 AC 传输特性,并使用后处理器生成开环增益 (AOL) 和噪声增益 (1/β) 曲线(图 2)。
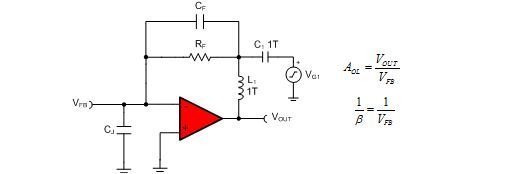
图 1:中断互阻抗放大器的反馈并生成 AOL 和 1/β 曲线
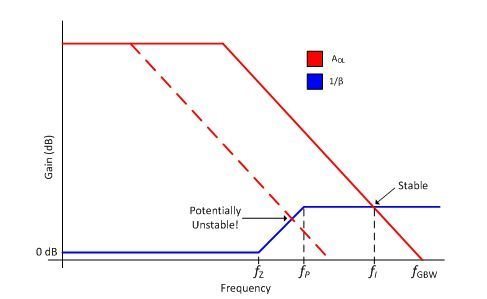
图 2:典型互阻抗放大器电路的 AOL 和 1/β 曲线图
1/β 曲线上有 3 个关注点。首先,在以下频率位置有一个零点:
在该频率以上,1/β 曲线以每十倍频程 20dB 的速率增加。接下来,在公式 2 频率位置有一个极点:
这会导致 1/β 曲线“变平”。最后,1/β 曲线将在以下频率位置与 AOL 曲线相交:

在公式 5 中,fGBW 是运算放大器的单位增益带宽。为保持稳定性,AOL 曲线必须在 1/β 曲线变平时与 1/β 曲线相交(假设是一个单位增益稳定的运算放大器)。如果 AOL 曲线在 1/β 曲线上升时与 1/β 曲线相交(如图 4 中虚线所示),电路可能会震荡。这可为我们带来以下规则:

将 fI 和 fp 的公式带入该规则,并求解单位增益带宽,我们可得到以下实用公式:
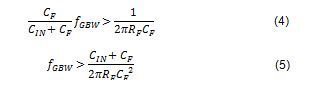
公式 5 消除了为互阻抗放大器设计选择运算放大器时的一道难题。选择具有足够带宽的运算放大器,不但可确保获得足够的信号带宽,而且还有助于避免潜在的稳定性问题!
设计实例
现在,我把这个过程运用在设计实例中,并对比采用两个运算放大器时的电路性能。一个运算放大器符合我们所计算的增益带宽要求,另一个不符合。该设计实例的要求如表 1 所示。

表 1:互阻抗放大器的实例性能要求
首先,我们计算可使电路稳定并达到带宽目标的最大反馈电容:
下一步,我们将确定放大器反相输入端电容。由于我们还没有为电路选择运算放大器,因此我们不知道 CD 和 CCM2 的值。记住,我在第 1 部分中建议将 10pF 作为该电容的合理电容估计值。
最后,我们可计算运算放大器的增益带宽要求:
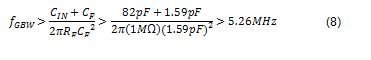
在该实例中,我将对比表 2 中所列的两个运算放大器:
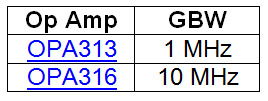
表 2:设计实例中两个运算放大器的增益带宽积对比
从前面的计算中我们知道,这两个运算放大器中的一个 (OPA313) 不具备电路所需的足够带宽。但实际上,这怎么会影响电路工作呢?
在Part2中,我不仅创建了一个设计实例(使用该过程选择可满足这些电路需求的运算放大器),而且还确定了所需的运算放大器带宽是 5.26MHz。Part3

表 1:互阻抗放大器的实例性能要求
现在,我们将对比两个运算放大器:一个符合要求,另一个不符合。

表 2:设计实例中两个运算放大器的增益带宽积对比
## 相位裕度对比
相位裕度是一个稳定性指标,可在环路增益等于 0dB 的位置将放大器环路增益 (AOL * β) 相位与 180 度相比。0 度相位裕度表明负反馈已经变成正反馈,说明系统不稳定。相位裕度可使用第 2 部分(图 1)的电路进行测量,其可中断反馈环路。在 AOL * β 电压幅值等于 0dB 的频率位置可测量 AOL * β 电压的相位(Vout 探针)。
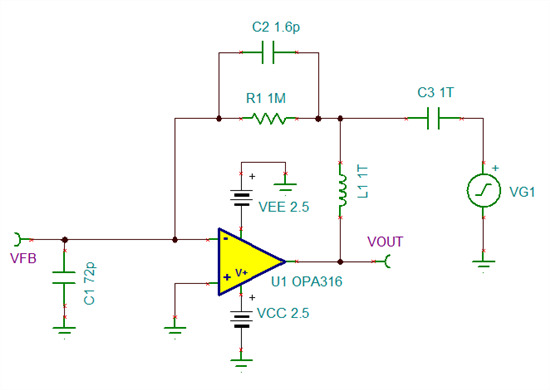
图 1:用于评估相位裕度的 TINA-TI™ 仿真原理图
图 2 是在 Tina-TI 中使用 OPA316 得到的 ac 传输特征仿真结果。从游标位置我们可以看到在 232.455 kHz 下 AOL * β = 0dB 时,相位裕度为 66.66 度。
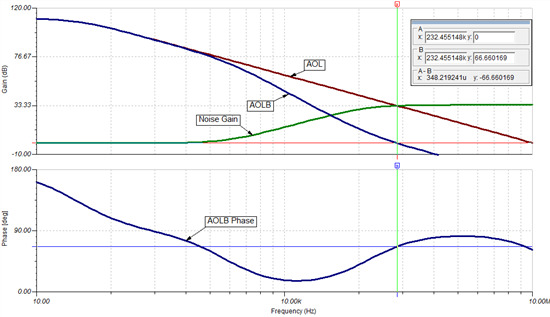
图 2:用于确定相位裕度的环路增益波特图
重复 OPA313 的这一分析可得到 31.65 度的相位裕度。从技术上讲,该部分在这一相位裕度下是稳定的,但它不会被视为稳定的设计。如果生产了大量这样的电路,有一些可能会因运算放大器技术参数的容差问题而不稳定。
阶跃响应对比
降低的相位裕度还会产生其它影响。例如,它可导致电路阶跃响应中的过冲和振铃问题。为说明这种影响,我使用瞬态仿真在电路输入端应用了 1uA 电流阶跃 (IG1),并测量了趋稳到 0.1% 理想值所需的时间。
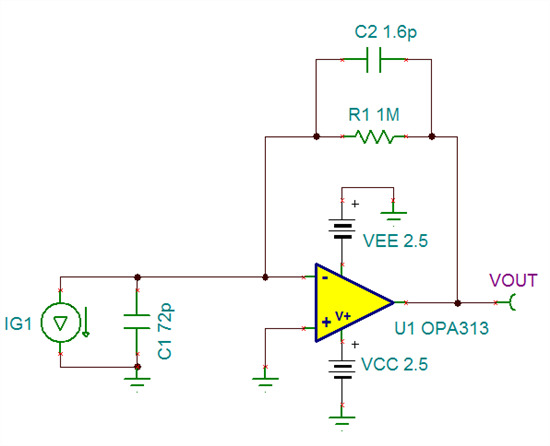
图 3:将 1uA 电流阶跃应用到输入端,以仿真阶跃响应
OPA316 的阶跃响应不仅表现出最低的过冲,而且还在 13μs 内趋稳至 0.1%。相反,OPA313 则在响应过程中表现出显著的过冲和振铃,需要 75μs 才能趋稳到 0.1%。
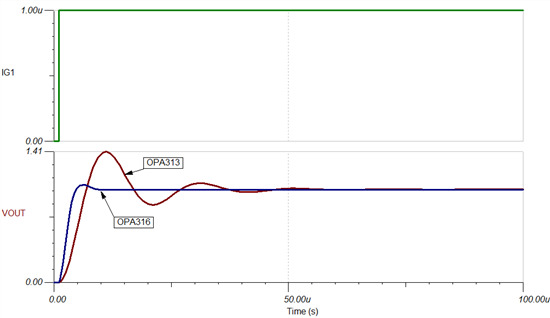
图 4:用于 1uA 输入电流阶跃(绿)的 OPA316(蓝)和 OPA313(红)的阶跃响应
幅值响应对比
最后,降低的相位裕度会引起电路传输函数峰值。图 5 是两个运算放大器的幅值响应。OPA313 的传输函数出现了 5dB 的增益峰值,这可能是无法接受的。更糟的是,使用 OPA313 时的 -3dB 位置是 78.47kHz。
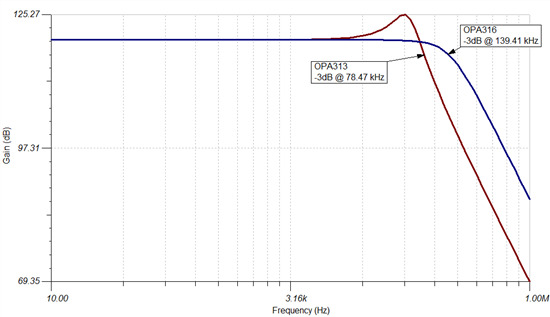
图 5:使用 OPA313(红)和 OPA316(蓝)构建的互阻抗放大器的频率响应对比
另一方面,OPA316 的传输函数不仅没有出现峰值,而且 -3dB 位置为 134.41kHz。
结论
对比计分板显示:OPA316 更符合我们的设计要求:

但这并不奇怪!我们的这 3 个步骤得到了 5.26MHz 的最小增益带宽要求。如果低于该值,电路稳定性、趋稳时间与带宽都会受到影响。希望本系列文章所介绍的这 3 个步骤将有助于您为您的互阻抗放大器快速选择合适的运算放大器,或者至少能帮忙将TI 1375 种选项缩小到一定的范围!
作者:John Caldwell
来源:TI社区


 谢谢分享!
谢谢分享! 



 /2
/2 
