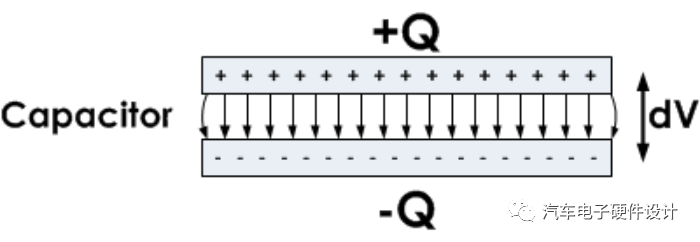
电容是身体以电荷(Q)的形式存储电能的能力。实际的电阻器总是表现出电容作为寄生特性。根据应用,电阻电容可能很容易被忽略,尤其是在直流电路中。在某些应用中,例如缓冲电阻器,电容寄生效应实际上是一种理想的效应。另一方面,寄生电阻电容可能是高频交流应用中的一个重要因素,会产生不良影响。其原因是具有寄生并联电容的电阻器的阻抗会随着施加频率的增加而降低。频率越高,阻抗越低,这意味着电阻器在高频下不再被视为恒定元件,
电容器和电阻器 功率负载可分为两种类型:实际(或电阻)负载和无功负载。实际负载用于将电能转换为热能。理想电阻器是纯电阻负载,这意味着施加到电阻器上的所有电能都以热量的形式耗散。另一方面,无功负载将电能转换为磁场或电场,并在将其返回到电路的其余部分之前将其临时存储。无功负载可以是电感性的或电容性的。电感负载以磁场的形式存储能量,而电容负载以电场的形式存储能量。
因此,理想电阻器和理想电容器之间的主要区别在于,电阻器将电能作为热量耗散,而电容器将电能转化为电场。理想电阻器的电抗为零,因此它们的电容也为零。不幸的是,电气设备在实践中并不理想,即使是最简单的电阻器也有轻微的寄生容抗。
寄生电容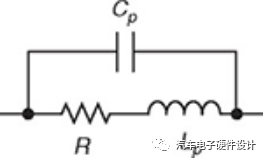
当需要纯电阻负载时会使用电阻器,因此电容通常是一种不需要的副作用,在这种情况下,它被称为“寄生电容”。所有实际电阻器都或多或少地表现出寄生电容,具体取决于电阻器的设计和结构。交流电路中的寄生电容可能会导致系统模块之间出现不必要的耦合,或者可能是导致高频电路响应延迟的原因。有专门为高频使用而设计的电阻器,它们被宣传为低电容电阻器,但是在数据表中通常很难找到电容的准确数字。
计算电抗和电容 在交流电路中,电阻抗是在施加电压时电路对电流通过的阻力的量度。由于寄生电容与电阻并联(电容分流电阻),因此这种电阻的复阻抗由并联公式给出:
Z=Z_R·jX_CZ_R+jX_C
其中Z是复阻抗,R是电阻,X是电路的电抗,j是虚数单位。在本文中,假设实际电阻器的寄生电抗是纯电容性的,因此电抗为:
X_C=-1ωC
因此,具有纯电容寄生效应的电阻器的复阻抗为:
Z=-R·j1ωCR-j1ωC
其中ω是角频率,C是电阻器的寄生电容。
对于直流或低频应用,我们通常只关心这个复阻抗的大小。可以使用以下等式计算阻抗的大小:
|Z|=1√(1R)^2+(2pifC)^2
式中:
R=以欧姆为单位的电阻
f=以赫兹为单位的频率
C=以法拉为单位的电容。
进一步分析上述方程可以看出,具有电容寄生效应的电阻器的总阻抗随着电压频率的增加而减小。这种降低通常可以忽略不计,但在某些应用中可能会变得非常显着。
不同电阻的电容 如前所述,制造商很少提供其电阻器的典型电容值。作为一般规则,SMD(表面贴装)电阻器的寄生效应比通孔电阻器低得多。原因在于,即使是引线导体也具有一定的电荷储存能力。将电阻器连接到电路其余部分的金属引线就是这种导体的一个例子。引线越长,可以存储的电荷越多,寄生电容就越高。因此,引线越短,在给定电阻器中可以看到的寄生效应越小,这就是SMD电阻器具有更少寄生效应的原因。
如果需要低电容,则电阻器应尽可能小且紧凑。应避免使用绕线电阻器,因为绕组会产生线圈间电容,这使得它们在 50kHz以上时无法使用。碳型电阻器的最高可用频率约为1MHz。另一方面,箔电阻器具有出色的高频使用特性,其电容通常小于0.05pF,这使得它们能够在高达100MHz的频率下正常工作。
寄生效应发挥作用的应用 寄生效应在高频时最为突出。例如,当考虑所有寄生效应时,在100MHz下具有0.05pF电容的金属箔1.0kΩ电阻器实际上会表现为0.9995kΩ电阻器。这是电阻器具有良好频率响应的示例。
相比之下,由于电感和电容寄生效应,线绕电阻器只能在高达50kHz的频率下使用。即使使用双线(无感)绕组方法,线圈间电容也会限制最大可用频率。
一些对寄生效应特别敏感的应用是:高频放大器电路、GHz时钟发生器和微波电路。
利用电容性寄生效应的电路示例是缓冲电阻器,用于保护开关元件(开关和晶闸管)免受电流切断期间感应负载(如电动机)产生的电压尖峰的影响。这些通常被制成双线绕线电阻器以降低电感。对于缓冲器应用,电阻器的设计使电容与电阻器串联,而不是像标准寄生电容那样并联。
本文由编辑推荐,原出处:https://www.eet-china.com/mp/a121762.html




 /2
/2 
