早在初中时,我们就学习过多元一次方程组的求程。
所谓多元一次组指的是含有有个未知数,并且含有未知数的项的次数都是1方程组。
一个简单的例子:
学校的篮球数比排球数的2倍多3个,足球数与排球数的比是2:3,三种球共48个,求三种球各有多少?
假设篮球个数为x1,排球个数为x2,足球个数为x3,
根据题目有以下的关系式成立:
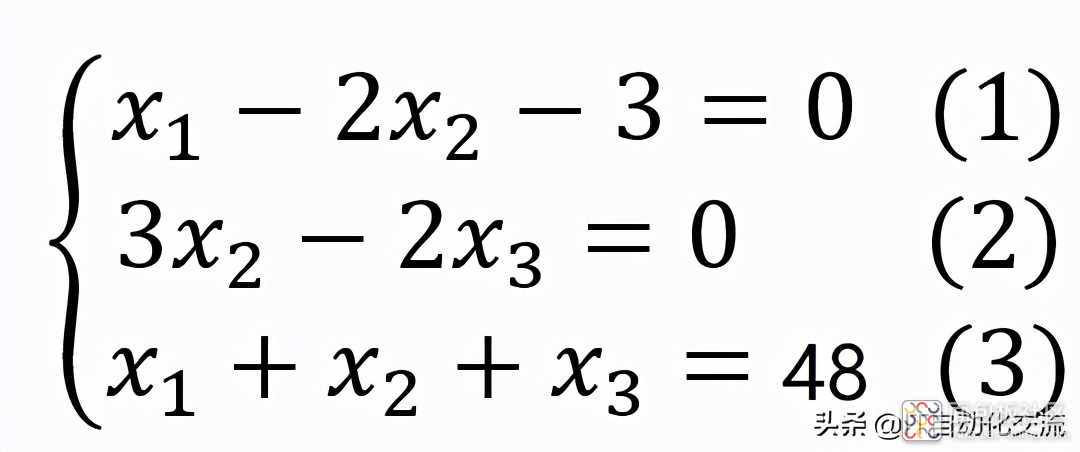
图1. 多元一次方程组
对于多元一次方程组,最常用消元法来进行求解。
思路是经过各个方程组之间的线性运算,消去一些未知数,最终得到一个未知数的方程。
根据该方程解出未知数,再代回其它方程得到其它未知数的值。
整个过程非常繁琐,一不小心就会出错;
矩阵运算
在学习了矩阵运算之后,这一求解过程可以化为矩阵运算而大大简化;
跟初等数学里面学习的加、减、乘、除运算规则一样,伟大的数学家们也为矩阵运算制定了一些规则。
对于矩阵的加、减,限于文章篇幅,在此不作赘述。
对于矩阵的乘法,有以下的规则:
设有一个m行s列的矩阵表示为
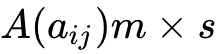
,
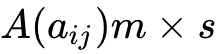
一个s行n列的矩阵表示为
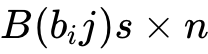
,
则矩阵A左乘于矩阵B所得到的矩阵C是这样一个矩阵: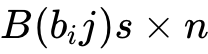
(1) 行数与(左矩阵)A相同,列数与(右矩阵)B相同,即C=
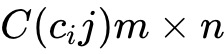
(2) C的第i行第j列的元素由A的第i行元素与B的第j列元素对应相乘,再取乘积之和。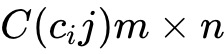
比如,两个矩阵:
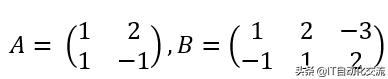
A、B矩阵
计算
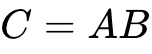
,从规则(1),可以知道C是2行3列的矩阵。
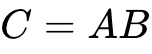
每个元素的数值由规则(2)计算得到,比如:
第0行0列的数值为:
c00=1*1+2*-1=-1;
第0行1列的数值为:
c01=1*2+2*1=4;
依次算出各元素的数值,并表示为矩阵,得到:
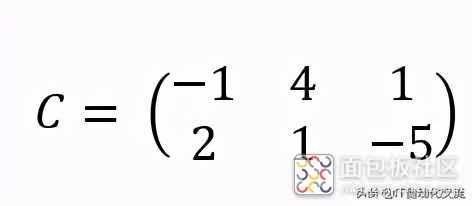
C=AB
对图1的多元一次方程组,我们做一些变形,
并把未知数表示为3行1列的矩阵,可以得到:
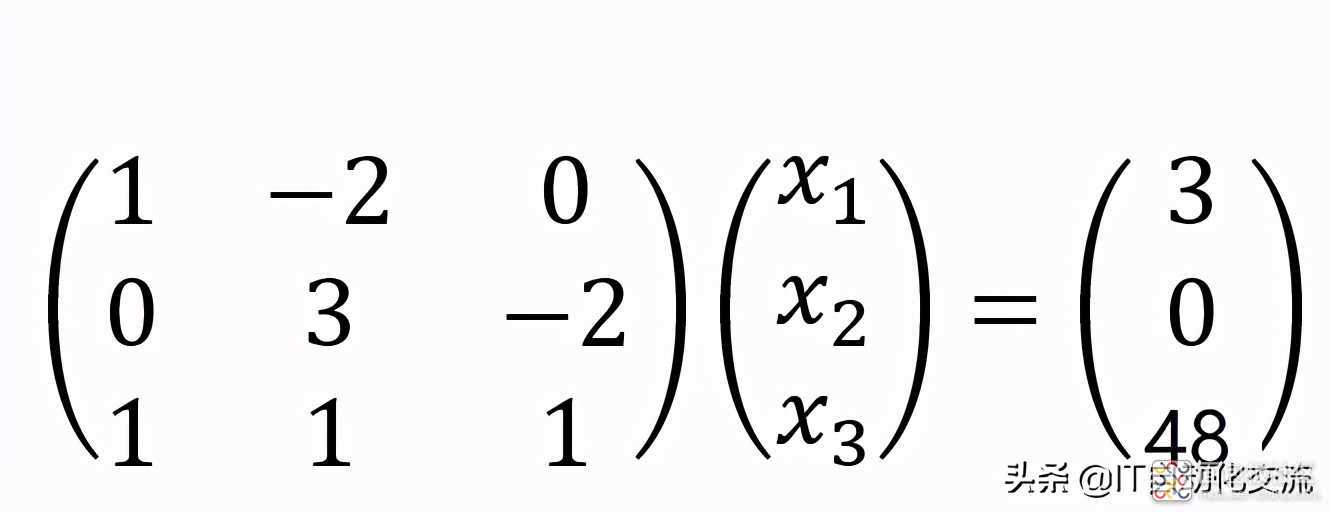
矩阵表达
表示为:
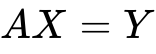
,然后就可以经过矩阵运算求解方程组。
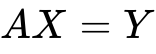
左右两边同时左乘A的逆矩阵,得到:
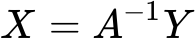
。
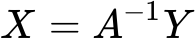
N年前,matlab还能随意使用,做矩阵运算非常只是几条命令的事情,非常简单。
在被matlab抛弃的日子里,虽然对matlab还怀有深深的眷恋,无奈落花有意、流水无情;
我只能退而求其次用python来排遣寂寞。
利用,以下python脚本,
import numpy.matlibimport numpy as np A=np.array([[1,-2,0],[0,3,-2],[1,1,1]]) Y=np.array([[3],[0],[48]]) X=np.matmul(np.linalg.inv(A),Y);
复制代码矩阵运算在电路计算、分析中的应用
在线性电路中,首先通过电路理论得到电路的线性方程组。
把线性方程组的求解转换为矩阵运算。
再用python编写脚本进行矩阵运算,就可以算出电路中的各电气参数;
如下图的电路分析题目,求解i1和i2;
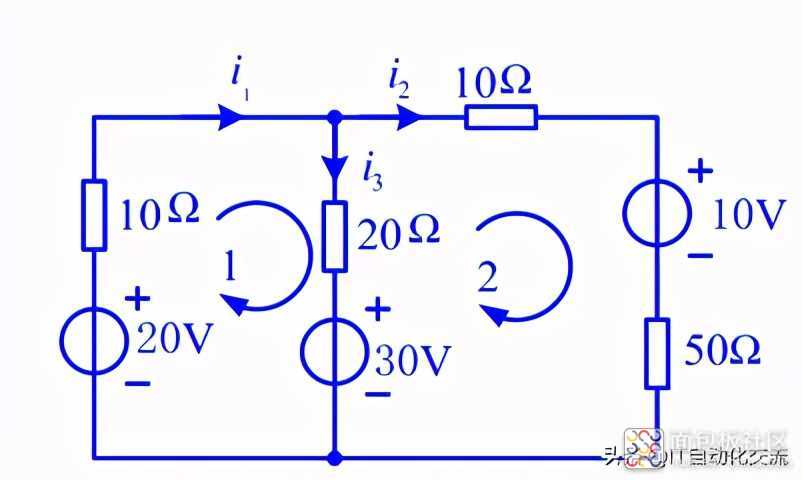
电路分析实例
根据网孔电流法,有:
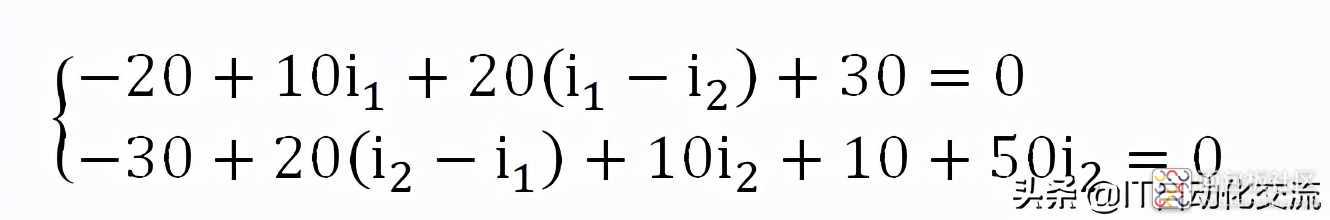
网孔电流法列出方程组
化简得到:
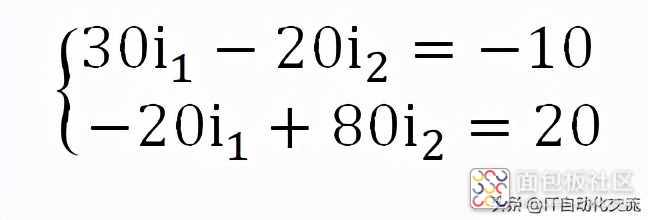
化简后的方程组
编写python脚本,
import numpy.matlibimport numpy as np A=np.array([[30,-20],[-20, 80]]) Y=np.array([[-10],[20]]) X=np.matmul(np.linalg.inv(A),Y)
复制代码总结
本文旨在介绍矩阵的概念、矩阵运算的规则,以及与多元一次方程组的关系。
并以一个简单的电路为例,介绍电路计算过程;
矩阵运算以及电路分析远不限于此,
另外通过符号的矩阵运算,可以得到电参数的解析表达式并对其化简,可以大大简化滤波电路的分析计算。
来源:物联网全栈开发






 /2
/2 
