一、为什么需要ECC内存?
因为硬盘的速度远远比不上CPU的速度,所以电脑在程序运行时CPU都会先把要执行的代码和各种数据从硬盘读取到内存(单片机这种小CPU除外),之后和内存交互数据,所以内存的稳定性很大程度上决定了电脑的稳定性。
但是在电脑的运行环境中,处处都包含着各式各样的干扰,包括EMI电磁干扰、电源纹波干扰等,这些干扰会导致内存在和CPU交互数据时发生比特翻转(某个0变成1),如果比特翻转发生在某些不重要的位置上,比如某张图片或者某个视频流里面,使用者很可能都感觉不到,但是一旦发生在某个代码里面,轻则导致软件报错或者闪退,重则蓝屏死机或hardfault,对于普通PC来说还算能接受,毕竟概率很小,但是对于服务器来讲,一次宕机可能会造成灾难性的损失,所以服务器往往会使用稳定性更高的ECC内存。
这里很多人有个误区,以为服务器用ECC内存是为了加快运行速度,其实相反,用ECC内存会损失掉内存百分之二到百分之三的性能,但这种内存可以主动发现数据传输过程中出现的错误,并将错误纠正,提高了整个系统的稳定性。
二、汉明码原理
为什么ECC内存能纠错呢?就是因为使用了汉明码编码。更准确来说,目前绝大多数ECC内存都是使用的汉明码来发现并纠错的。汉明码在一组数据中最多只能纠错1个比特或者最多发现2个比特的错误,超过2个比特的错误就有概率通过汉明码校验,这是前提,只有在这个基础上我们才能推出后面的结论。
汉明码原理总结来说就是奇偶校验+交集排除,奇偶校验负责检测错误,交集排除负责定位错误的位置。
奇偶校验:根据被传输的一组二进制代码的数位中“1”的个数是奇数或偶数来进行校验。以偶校验为例,在每组数据中增加一个奇偶校验位,若原始数据1的个数为奇数,那奇偶校验位就补1,若原始数据1的个数本身就是偶数那奇偶校验位就不用补1,用0代替。奇偶校验有个巧妙的地方,就是奇偶校验位本身也能被校验,这也是奇偶校验能和交集排除配合使用的一个必要前提。
交集排除:简单来说就是元素A若同时在集合B和集合C中,如果A、B、C都存在的话,那A一定在B∩C中。下面以一个4*4的数据举例说明。
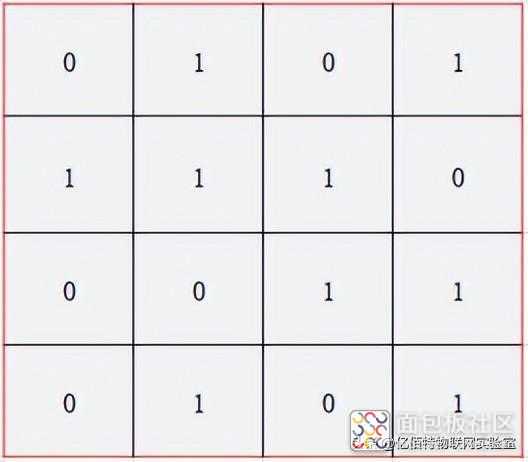
- 为了使用交集排除,先把4*4的数据分成下图4个区:
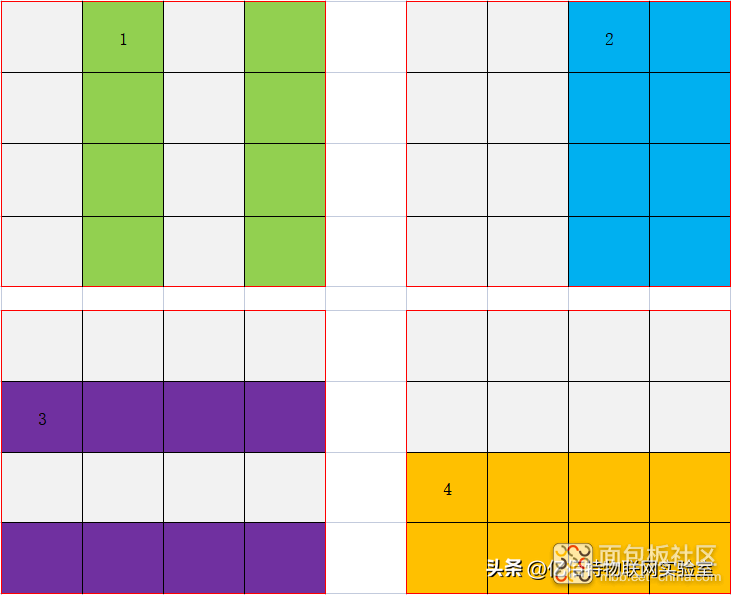
2. 在1区使用偶校验得出没有错误:
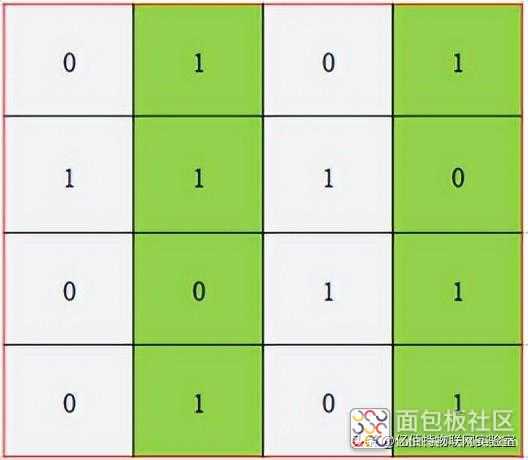
3. 在2区使用偶校验得出有错误:
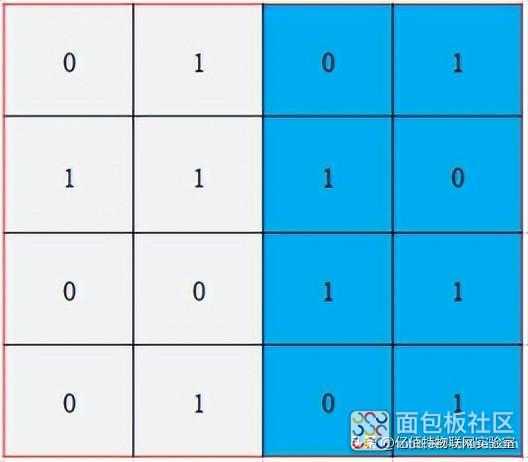
4. 在3区使用偶校验得出有错误:
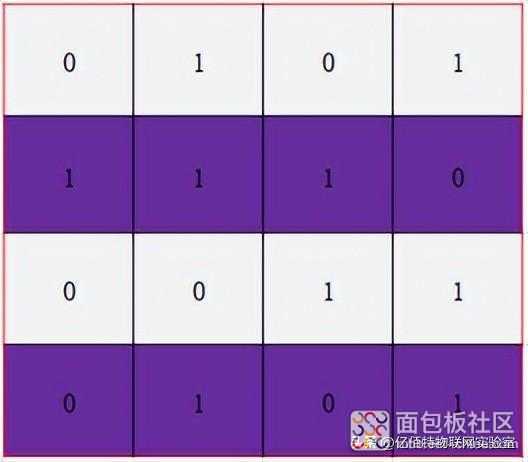
5. 在4区使用偶校验得出没有错误:
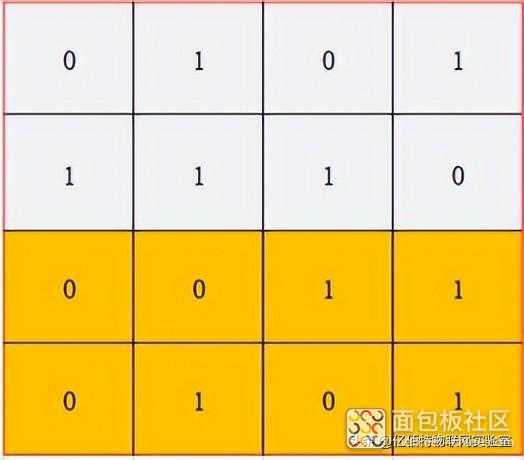
6. 综合2、3、4、5的结论就可以得出,错误数据同时在2区和3区,并且1区和4区没有错误,所以错误数据一定在如下(2,3)的位置,所以把(2,3)的1改为0就能得到正确的一组数据。
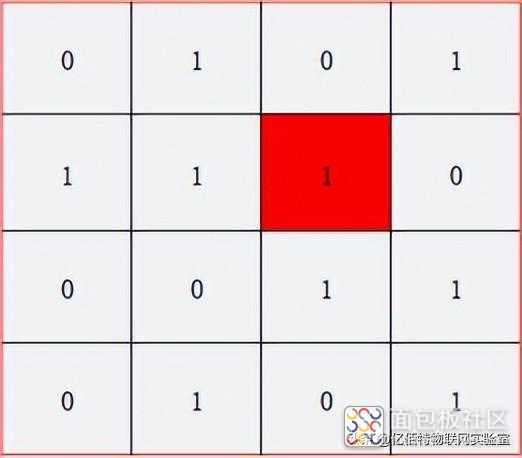
三、总结
以上就是汉明码最基础的原理,但这并不是汉明码被广泛运用在内存纠错的全部原因,因为单纯比纠错能力,它远远没有LDPC低密度校验码强,能被广泛运用的原因是汉明码能用极少的硬件电路实现(4*4的数据只需要5级异或门),而且有效数据比很高(一组数据只需要在2的整数次方的比特位置插入一个比特的校验位,有效数据比成指数级提高,当然一组数据越长超过2比特错误的概率也就越大),具体原理后面再分析。
来源:亿佰特物联网实验室






 /3
/3 
