为了将PWM信号转成直流,需要利用低通滤波器滤除PWM信号中的高次谐波信号。
多阶RC低通滤波是一种比较常用的方法,如下图的二阶RC滤波电路:
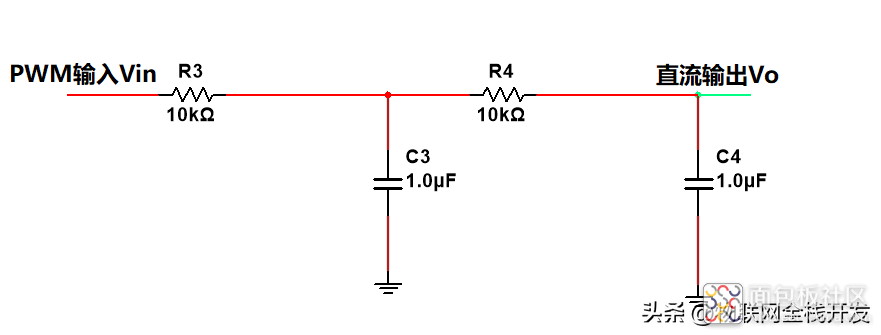
用于PWM转直流的二阶RC滤波电路
拉普拉斯变换
单位阶跃信号定义为:
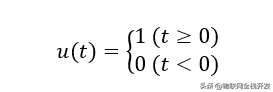
单位阶跃信号
其拉普拉斯变换定义为:
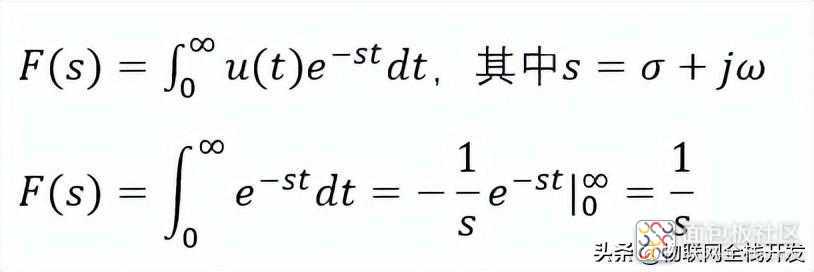
单位阶跃信号的拉普拉斯变换
如果PWM信号的高电平为VH,当输出高电平时,输出信号的拉普拉斯变换为:
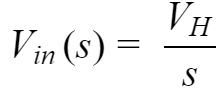
电容C3,C4在频域下的阻抗分别为
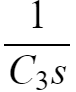
以及
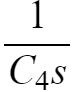
,得到频域下的等效电路和参数:
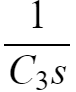
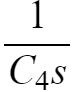
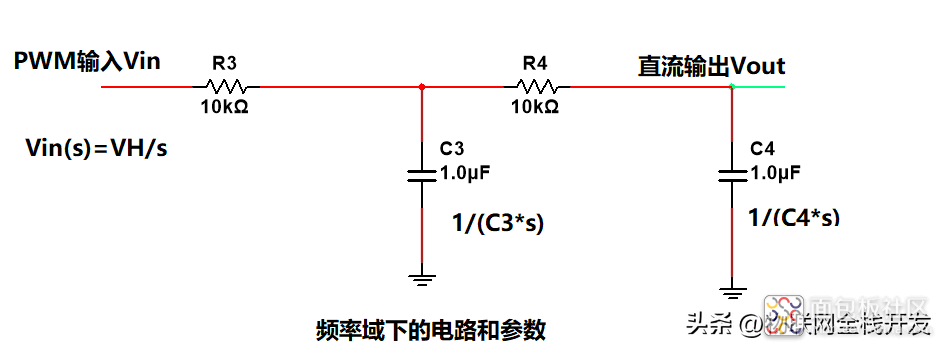
频率下的电路和参数
Octave符号运算
当输入信号
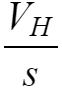
时,根据频域下的电路,可以计算出电容C4两端的电压。
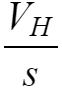
涉及到分式多项式的运算,运算量大,容易算错。
可以使用Octave的符号运算快速得到结果。
Symbolic符号运算包需要用到Python的SymPy库。
在Octave的命令行窗口,运行pkg install -forge symbolic,下载symbolic符号运算包,
再运行pkg load symbolic,加载symbolic符号运算包。
运行以下脚本:
syms R3 R4 C3 C4 s VHZC4=1/(C4*s);%电容C4的阻抗ZC3=1/(C3*s);%电容C3的阻抗Z1=R4+ZC4;%Z1为R4与C4串联Z2=ZC3*Z1/(ZC3+Z1);%Z2为C3与Z1并联Vo=VH/s*Z2/(Z2+R3)*ZC4/Z1;%C4两端的电压为Z2与R3分压之后,再由C4与R4分压simplify(Vo)%化简符号表达式
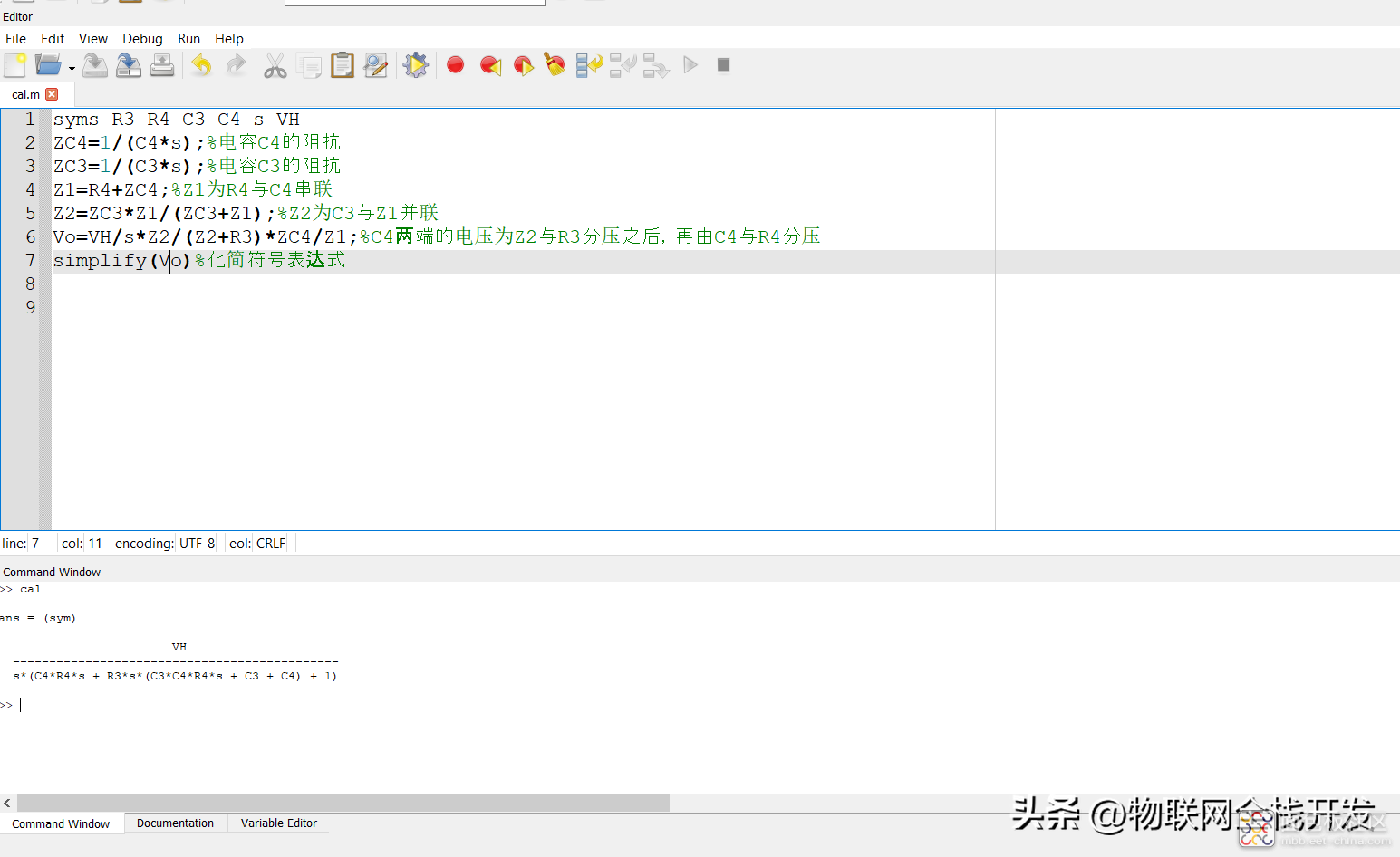
Octave符号运行过程
得到电容C4两端电压Vo(s)为:
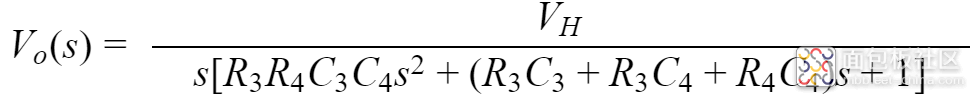
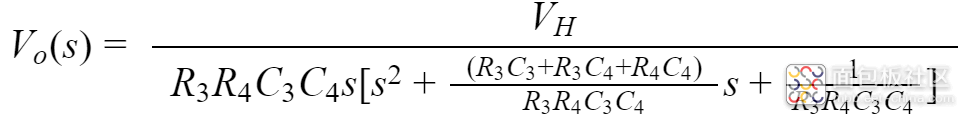
假设
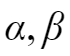
分别为方程
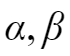
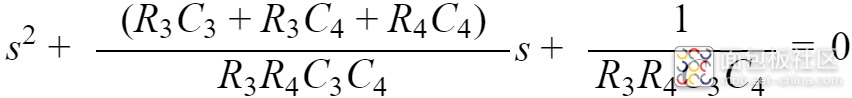
则根据韦达定理,有:
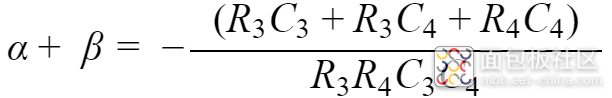
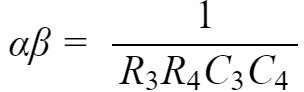
而
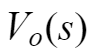
可以表示为:
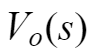
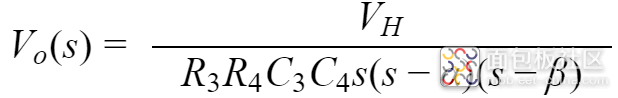
对于形如
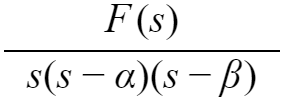
的多项式,
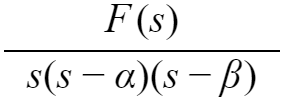
可以转换为:
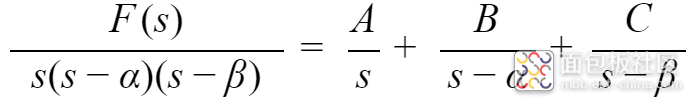
左右两边同时乘以s,得到,
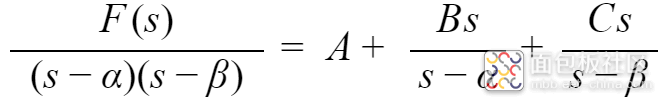
在上式中,令s=0,得到:
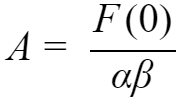
左右两边同时乘以
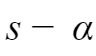
之后,令
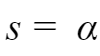
,得到:
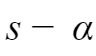
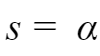
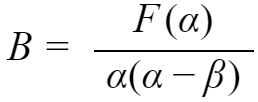
同样得到,
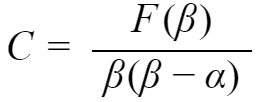
所以,
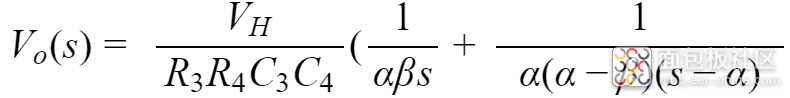
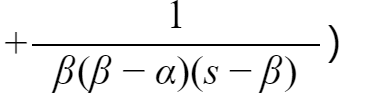
根据拉普拉斯的逆变换,

常见的拉普拉斯变换对
得到,C4两端的电压在时域的表达式为:
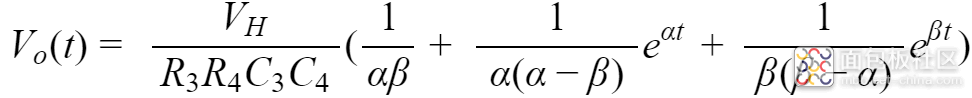
当R3=R4=10kΩ,C3=C4=1uF时,
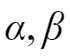
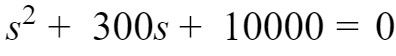
根据求根公式,得到,
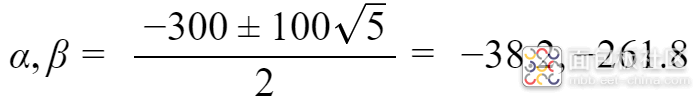
假设
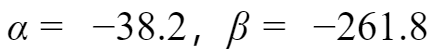
,
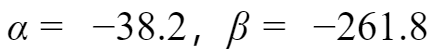
当PWM的频率为800Hz时,占空比为100%时,充电的最长时间为1.25ms,
此时,
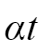
最大为-38.2*1.25ms=-0.04775<1,
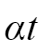
而
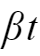
最大为-261.8*1.25ms=-0.32725<1,
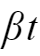

常见函数的泰勒公式展开
将函数
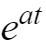
,
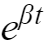
用泰勒公式展开,并保留至第二项;
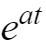
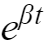
得到:
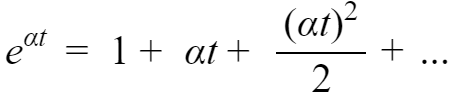
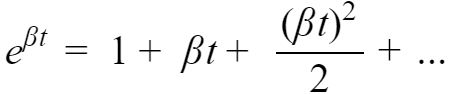
代入式2,得到:
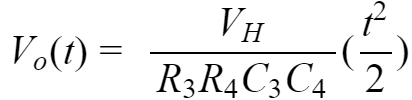
当考虑PWM输出一段时间之后,PWM在切换到高电平的瞬间,电容C4已经有一定的电压U0,则式1应该加到电容C4的初始电压,再经过拉普拉斯逆变换,得到,
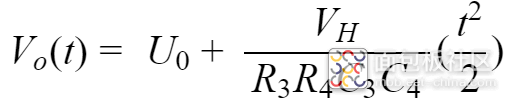
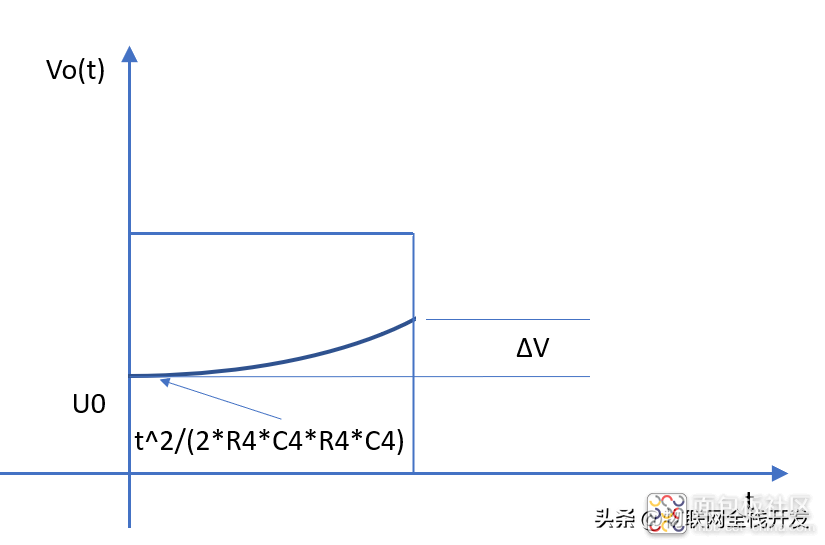
充电波形
当高电平为5V,占空比为50%时,纹波大小为:
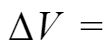
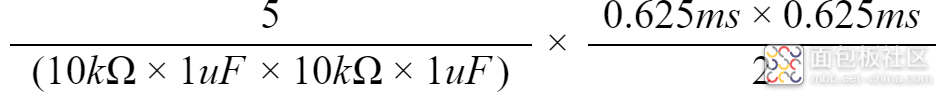
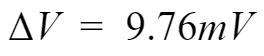
来源:物联网全栈开发






 /4
/4 

