简介
本应用指南介绍了在特定应用条件下门极驱动性能参数的计算方法。通过本应用手册得出的一些参数值可以作为选择一款合适驱动器的基本依据。
对于快速预览,公式1,4 及5 是最重要的。
所需驱动功率
驱动器是用来控制功率器件的导通和关断。为了实现此功能,驱动器对功率器件的门极进行充电以达到门极开通电压VGE_on,或者是对门极进行放电至门极关断电压VGE_off。
门极电压的两种电平间的转换过程中,在驱动器门极驱动电阻及功率器件组成的回路中产生一定的损耗。这个参数我们称为驱动功率PDRV。驱动器必须根据其所驱动的功率器件所需的驱动功率来选择。
驱动功率可以从门极电荷量QGate,开关频率fIN,以及驱动器实际输出电压摆幅∆VGate 计算得出:

如果门极回路放置了一个电容CGE(辅助门极电容),那么驱动器也需要对该电容进行充放电,如图1 所示:
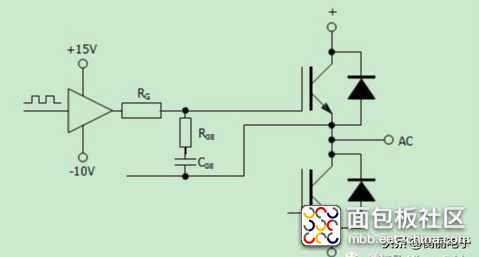
图1.带外接阻容的门级驱动
只要CGE在一个周期内被完全的充放电,那么RGE 值并不影响所需驱动功率。驱动功率可以从以下公式得出:
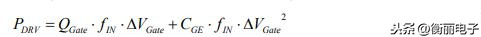
以上公式是在门极驱动电流不发生谐振的条件下得出的。只要这个开关过程是IGBT 门极从完全打开到完全关断或者反过来,则驱动功率并不依赖于门极电阻及占空比的变化而变化。接下来我们来看如何确定门极电荷量QGate。
门极电荷量
QGate绝不能从IGBT 或MOSFET 的输入电容Cies计算得出。Cies 仅仅是门极电荷量曲线在原点(VGE=0V)时的一阶近似值。功率半导体的门极电荷量曲线是极其非线性的。这就是为什么QGate必须通过对门极电荷量曲线在VGE_off 到VGE_on的区域内积分获得。
如果QGate 在数据手册中已给出,在实际应用中一定要注意该参数给定的电压摆幅条件。不同的电压摆幅条件下门极电荷量是不同的。举个例子:如果VGE 从0V 到+15V 条件下的门极电荷量是QGate,那么没有办法很准确的得到VGE 从-10V 到+15V 条件下的门极电荷量。
在这样的情况下,如果没有电荷量图表(QGate vs. VGE),则实测电荷量QGate是唯一的方法。图2 显示的是一张典型的驱动器开通过程的波形图。驱动器输出电流IOUT正在对功率器件的门极进行充电。因此,如图2 所示,输出电流曲线与时间轴围成的区域就是总的充电电荷量(见图4 所示的原理图)。积分时间应宽到足以涵盖整个电压摆幅(参照输出:GH,GL) 。积分时间包括驱动器输出电压至最终电压,或者是从驱动器开始输出电流至输出电流为零这段时间。

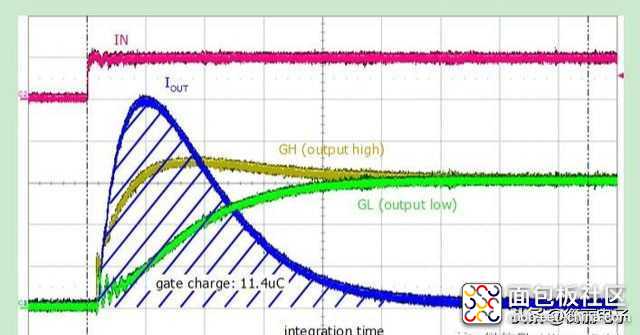
图2.用积分的方法来测量门极电荷量
必须注意输出电流是否出现振荡。在实际应用中,电荷量的测量值通常受电流振荡影响而变得不准确,其原因是过长的积分时间以及少量大数叠加而非大量小数叠加产生的不准确性。因此,强烈建议使用驱动电流无振荡的设置来对门极电荷量进行测量。
驱动器输出电流振荡或可导致驱动器单元产生额外的功率损耗,这些损耗是由于钳位效应及输出级和控制回路的非线性产生的。因此,驱动器最大可用功率通常是在输出电流不发生振荡的情况下得出的。
谐振门极驱动可以利用高频开关下的振荡现象来获得某种好处。但这种驱动方法不在本应用指南讨论范围内。
峰值驱动电流公式
门极驱动电路另一个重要的参数就是最大门极驱动电流IOUT,max。门极驱动电流IOUT,max必须足够大以便在最大电压摆幅及最小门极电阻条件下提供足够的驱动电流。其一阶最大值可以简写成:

若门极电流存在振荡现象,则建议在选择驱动器时,其峰值电流应满足IOUT,max> ÎOUT(1. Order)。如果门极电流的振荡表现出低阻尼特性的话就必须引起注意。此时,峰值电流电流会很大,且通常只能通过测量得到。
实践经验表明,在门极电流无振荡,且驱动电阻较小的情况下,电路中实际观察到的电流峰值低于ÎOUT(1. Order)的70%。门极电流的减小是由于门极回路中的寄生电感导致的。这个寄生电感在门极充电开始时限制电流的斜率。因此,在门极回路电流无振荡出现的情况下,对于驱动小阻值门极电阻,我们只需根据如下要求选择驱动器,驱动器的门极电流至少需提供0.7 倍的衰减因子:

在使用公式5 时,驱动器输出端的实际峰值电流需要进行实测以作确认。
举例:驱动器电压摆幅为25V(+15 / -10V),门极电阻为0.5Ω,IGBT模块门极内阻为0.2Ω,则驱动器提供的最大峰值电流至少应为25A。
实际应用中的0.7倍衰减因子的一个理论依据可以参照章节“最大驱动电流”。
输出电压摆幅的变化
门极驱动器的输出电压摆幅在输出功率范围内会有轻微的变化。这是因为驱动器高压隔离DC/DC 电源的外特性有些软所致。最边界的计算值是通过最大电压摆幅得出的。请在预期使用的功率范围内依据驱动器的数据手册得出电压摆幅,或者是在电路中进行实测。
严格来说,门极电荷量需在特定的门极电压摆幅下进行测量。如果门极电荷量是在较大门极电压摆幅(在低频下) 条件下得出,那么计算得出的驱动功率会比实际驱动功率大(在目标频率下)。如果目标精度低于5%,实际上没有必要去考虑这个因素的影响。欢迎注册论坛(www.21micro-grid.com),加入技术交流QQ群:电力电子技术与新能源 905723370,关注微信公众号:电力电子技术与新能源(Micro_Grid)
最大运行温度
除非另有说明,CONCEPT驱动器在–40°C 到85°C的温度范围内能输出全功率。如果没有关于降额说明,那么可以认为在全温度范围内都能输出全功率和额定电流。
温度等级是参考无强迫风冷,自然对流的环境温度而言。即使是中级的强迫风冷(通过风扇形成环流)能够强烈地改善驱动器的热传导—提高驱动器的可靠性。
最大开关频率
某些参数会影响最大可使用开关频率。首先,前面章节所讨论得出的输出功率。第二是门极电阻上的功耗变化。门极电阻越大,在给定频率下驱动器推动级的功耗就越小。第三是由于高开关频率而影响驱动器的温升。
图3 所示的是不同门极驱动电阻条件下,最大允许输出功率与开关频率的关系的曲线图。该图只适用某个具体的驱动器,并不是通用的。
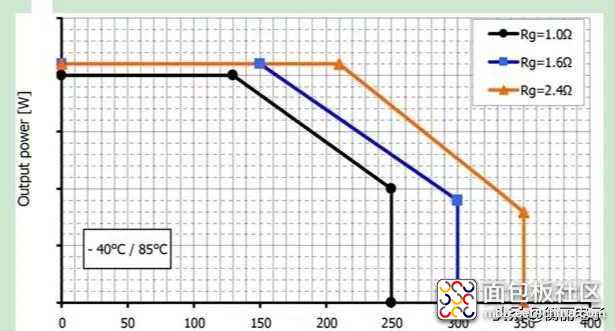
图3.最大允许输出功率与开关频率的关系
最大驱动电流
实际应用中,驱动峰值电流的计算理论来源于以下问题:
在没有振荡的情况下,门极回路中的实际峰值电流能达到多少?
以下分析仅专注于门极电阻的变化而其他参数不变。假设门极回路不发生谐振也就是门极电流的波形不发生振荡。图4所示为门极电路模型,由驱动器的推动级输出端GH,GL;独立的门极电阻Rg,on/off以及相应的杂散电感
Lg,on/off;以及功率器件回路中存在的杂散电感 Lgg组成。功率器件可以由一个常量电容建模而成。这是一个被简
化的模型,但是在门极充电过程的起始时刻是很合理的。门极充电起始时刻是最相关的阶段,因为充电电流在此刻达到最大。
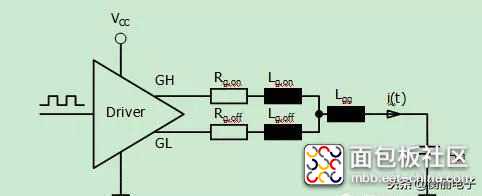
图4:门极驱动回路模型
门极电流i(t)由RLC 回路著名的二阶差分方程决定:

Lg 与Rg分别是开通和关断回路中L 与R 的总和。区分振荡与非振荡的边界是Lg,Cgg以及Rg比例。i(t)不振荡方程需满足以下阻尼条件:

得出电流波形不振荡的最小门极电阻计算公式为:

因此,在电流不振荡的前提下,最大峰值电流在临界阻尼条件下可以表示为峰值门极电流Îmax(non-osc):
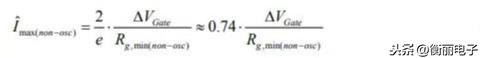
这里e 是欧拉常数。
请注意公式9只在非振荡条件下计算最大电流时是正确的。当Rg 大于Rg,min(non-osc)时,峰值驱动电流小于Îmax(non- osc)。对于大阻值的门极驱动电阻,可以按公式4计算门极电流。但是峰值门极电流也总是小于Îmax(non-osc)。因此,根据公式9来选择驱动器的带载能力(即驱动器最大输出电流)是完全可以的。必须根据门极回路设置及功率器件来选择合适的 Rg,min(non-osc)。欢迎注册论坛(www.21micro-grid.com),加入技术交流QQ群:电力电子技术与新能源 905723370,关注微信公众号:电力电子技术与新能源(Micro_Grid)
理论上推导出来的Îmax(non-osc)的衰减因子0.74在实际应用中会受到以下限制进一步减小,如:驱动器的开关速度,门极回路传输线的属性以及驱动器支撑电容的内部时间常量。因此,实际应用中推荐衰减因子值0.70 和理论的
出的值0.74 的效果是一致的。
举例:如果门极输出电压摆幅∆VGate=25V,门极回路的电感量为20nH,并假设IGBT 的输入电容量是30 nF,那么:
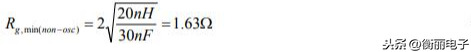
如果门极电阻阻值小于1.63Ω,门极电流就会开始震荡。假设这门极驱动上并不存在这个振荡。那么Rg=1.63Ω
时最大非振荡门极电流为:
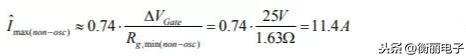
对于更大阻值的门极电阻,衰减因子由0.74上升至1.0,相应的门极电流将减小且总小于Îmax(non-osc)。
转载自网络,仅供学习交流使用,如有侵权,请联系删除。







 /3
/3 
