时域分析与频域分析是对模拟信号的两个观察面。
时域分析是以时间轴为坐标表示动态信号的关系;频域分析是把信号转变为以频率轴为坐标表示出来。
一般来说,时域的表示较为形象与直观,频域分析则更为简练,剖析问题更为深刻和方便。
目前,信号分析的趋势是从时域向频域发展。然而,它们是互相联系,缺一不可,相辅相成的。
对于这几天提到的PWM滤波电路,如果使用一阶R、C低通滤波电路,
在时域进行分析时,可以通过电容的电压和电流的微分关系得到一阶常微分方程,求解该方程得到电容两端的电压表达式,能比较清楚地分析电路的充、放电过程,计算得到纹波系数;
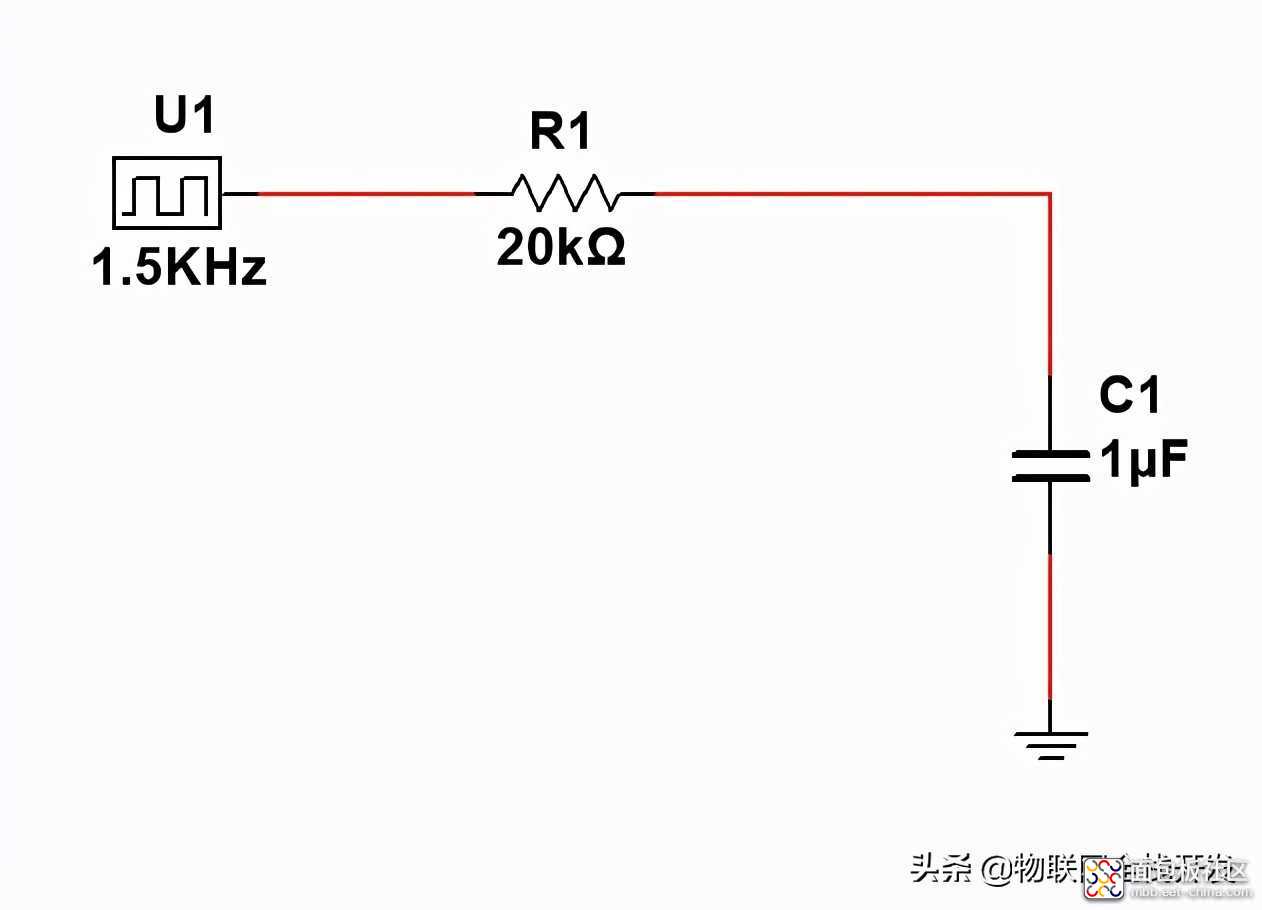
一阶R、C低通滤波电路
分析得到,纹波系数比较大 ,为了得到小于0.5%的纹波系统,对于频率为1.5KHz的PWM信号,R、C滤波电路的时间常数需要大于100ms左右。
为此,我们再加上一级R、C低通滤波电路以降低纹波,得到如下图所示的二阶R、C低通滤波电路,在时域分析求解微分方程变得非常困难,难以得到电压的解析表达式。
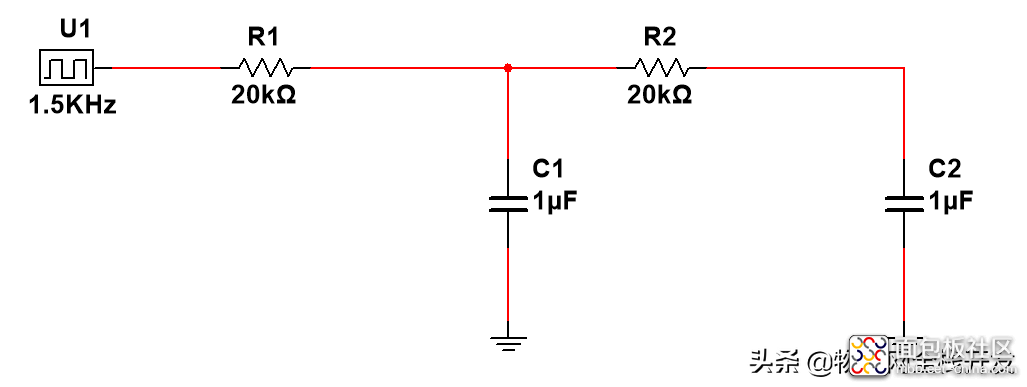
二阶R、C低通滤波电路
因此,我们需要在频率域进行分析。
三角函数的积分公式有以下三角函数的微、积分公式:
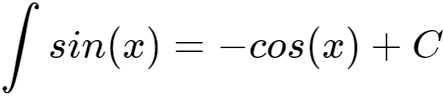
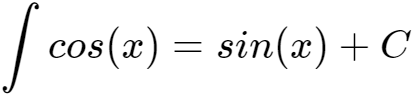
对于频率为某个频率f0的整数倍的两个正弦信号在一个周期内的定积分计算为:
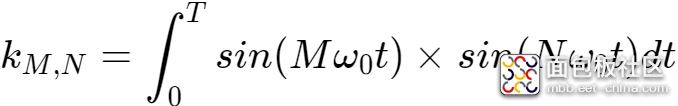
上式中,
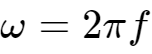
,M,N为正整数;
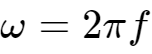
根据三角函数的积化和差公式,得到:
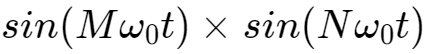
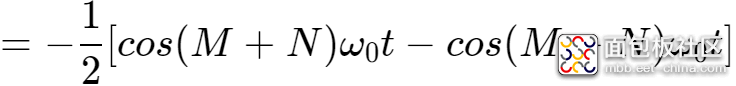
从而,当
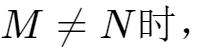
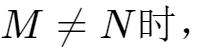
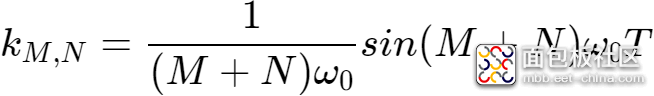
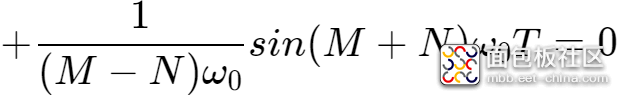
当
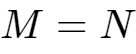
时 ,
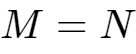
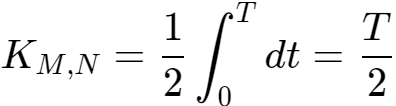
因此,对于一组以频率f的整数倍频率的三角函数,具有正交性特点。
即这组三角函数中任意两个不同函数的乘积在一个周期的积分为0。
PWM信号的傅里叶级数展开对于周期为T,占空比为
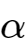
,低电平为0V,高电平为U的PWM信号。
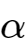
PWM信号平移成偶函数,在一个信号周期内的数学表达式为:
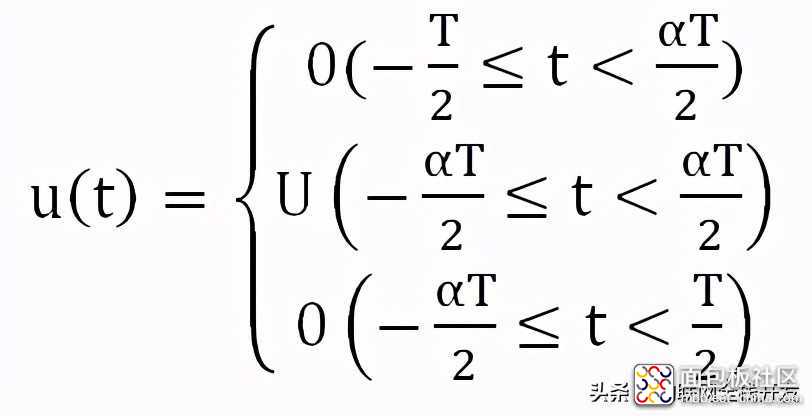
PWM信号的数学表达式
波形如下:
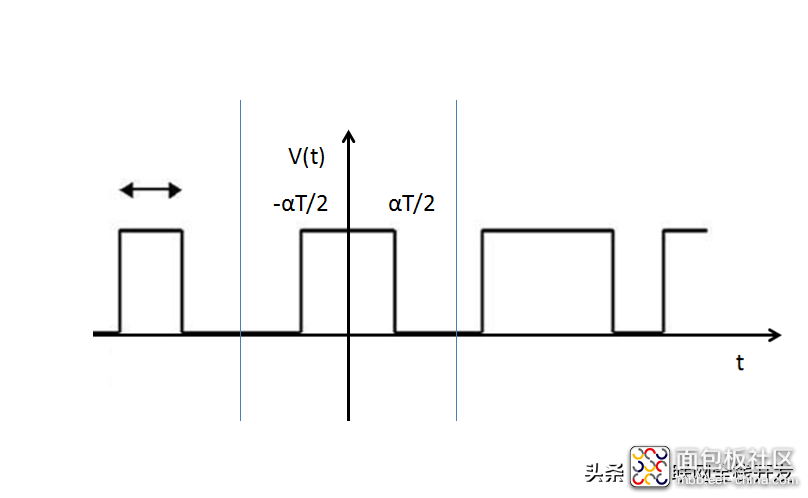
PWM信号波形
可以认为该PWM信号由直流分量,以及频率为PWM频率整数倍的各种余弦波而成。
数学公式表示为:
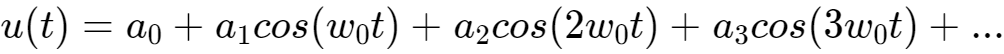
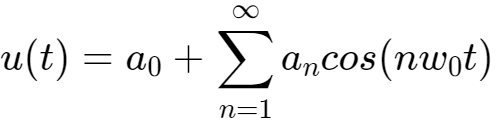
将上式左右两边同时乘以
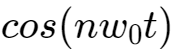
,并在PWM的一个周期内进行积分,根据三角函数的正交性,得到:
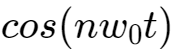
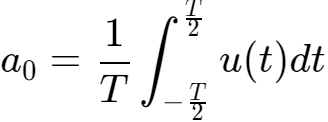
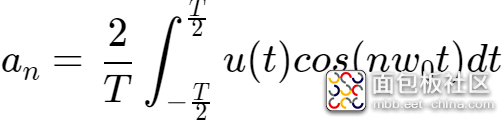
将u(t)代入,得到:
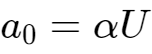
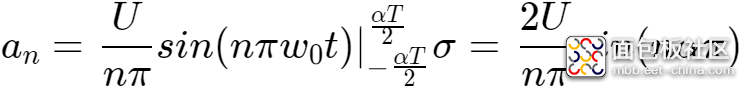
最终得到PWM信号的傅里叶级展开式为:
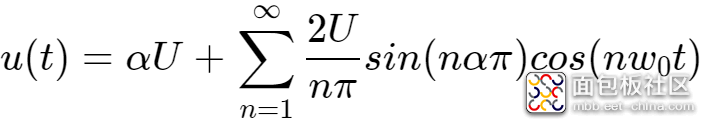
以占空比为50%,高电平U=1V的PWM为例,其直流成份以及前几次谐波的幅度如下:
n | 幅度 |
0 | 0.5 |
1 | 0.64 |
2 | 0 |
3 | -0.21 |
4 | 0 |
5 | 0.13 |
6 | 0 |
7 | -0.09 |
直流分量以及前7次谐波分量叠加的波形如下:
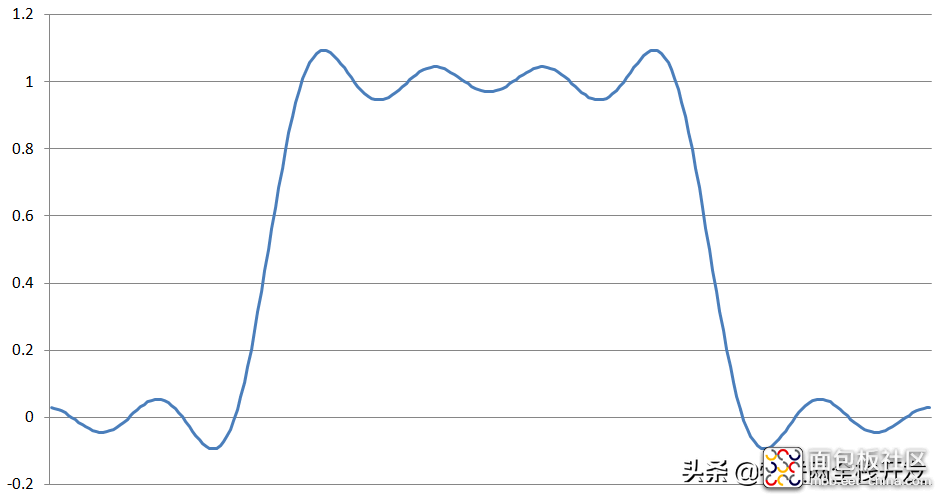
PWM的直流分量以及前7次谐波分量叠加波形
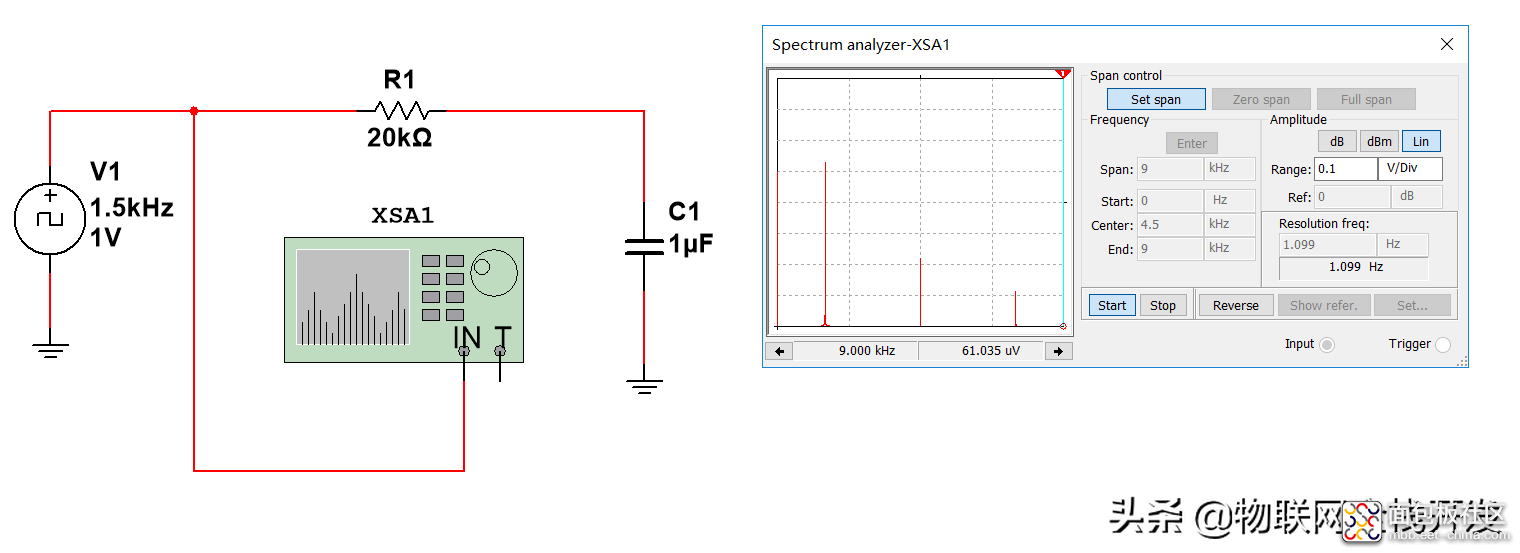
通过multisim仿真软件的频谱分析仪分析PWM信号的频谱
一阶R、C滤波电路的频率特性
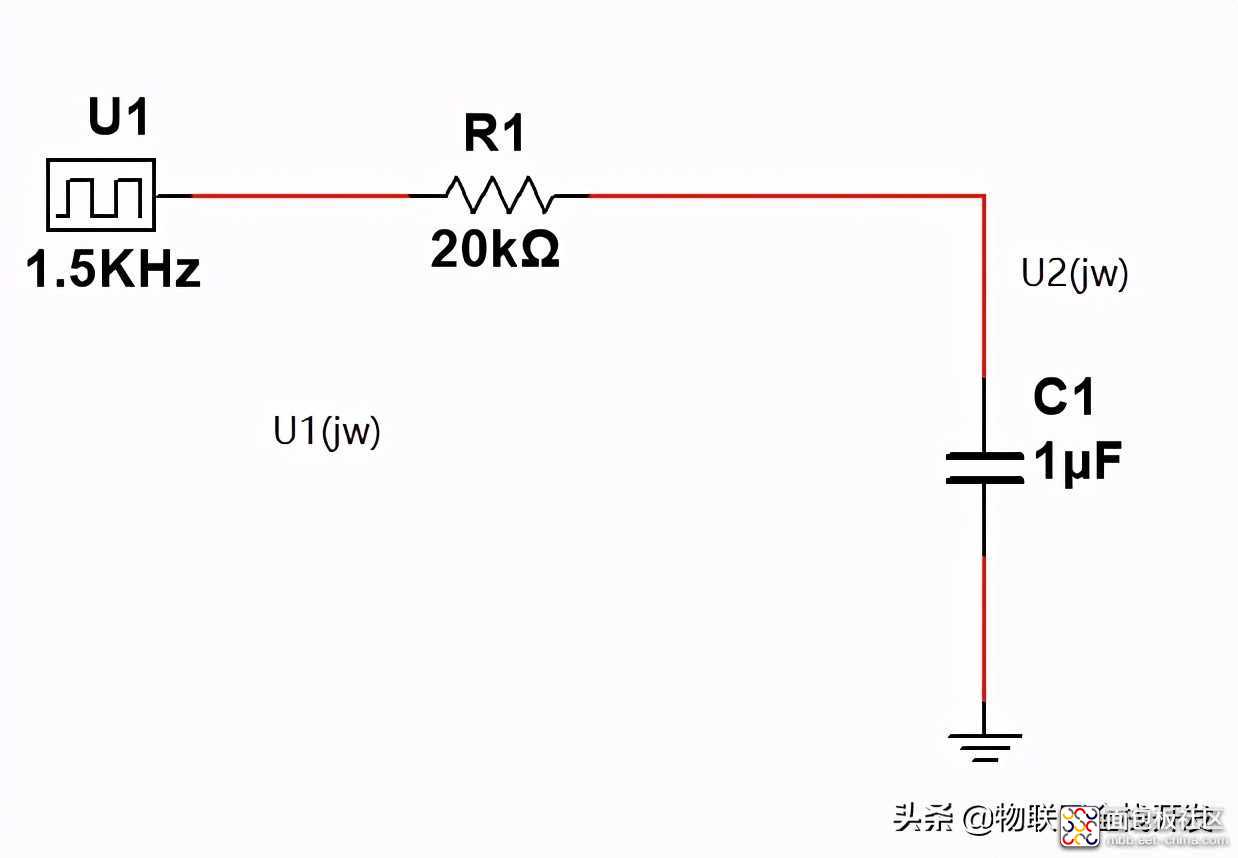
一阶R、C滤波电路
在频域分析上述电路,电阻R1的阻抗为R1,电容C1的阻抗为
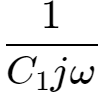
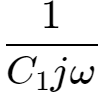
输入输出传递函数
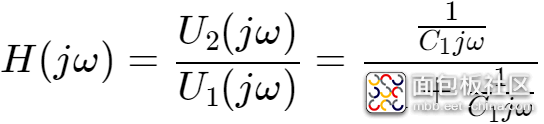
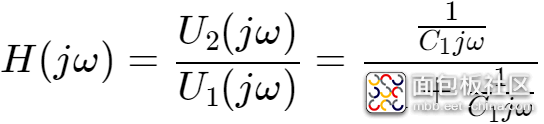
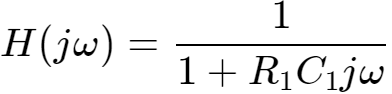
幅值增益
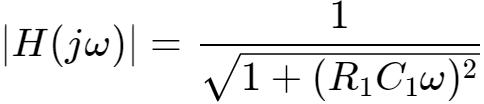
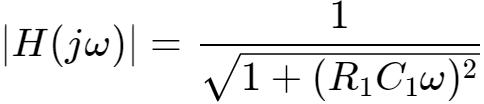
当输入U1为式1定义的PWM信号时,输出U2表示为:
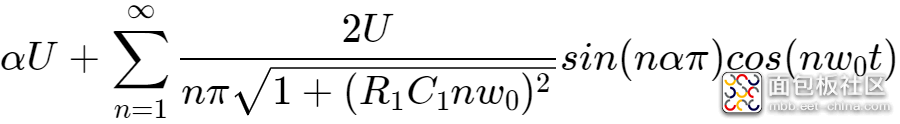
为了达到0.1%的精度,考虑第1次谐波分量的幅度与高电平相比<0.01%。
即有:
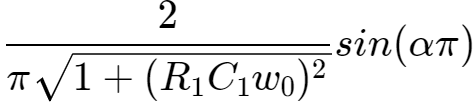
当
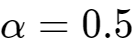
时,该值最大,所以要求:
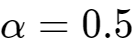
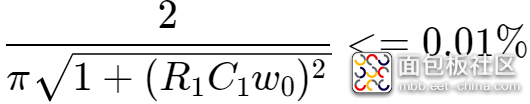
解得:
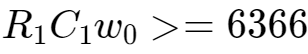
当PWM的频率为1.5KHz时,
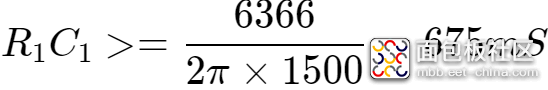
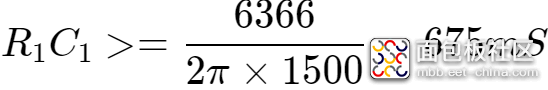
也就是,比如高电平为1V,频率为1500Hz,占空比为50%的PWM信号,
当R1、C1的时间常数大于675mS时,1次谐波的分量的幅度小于0.1mV。
二阶R、C滤波电路的频率特性
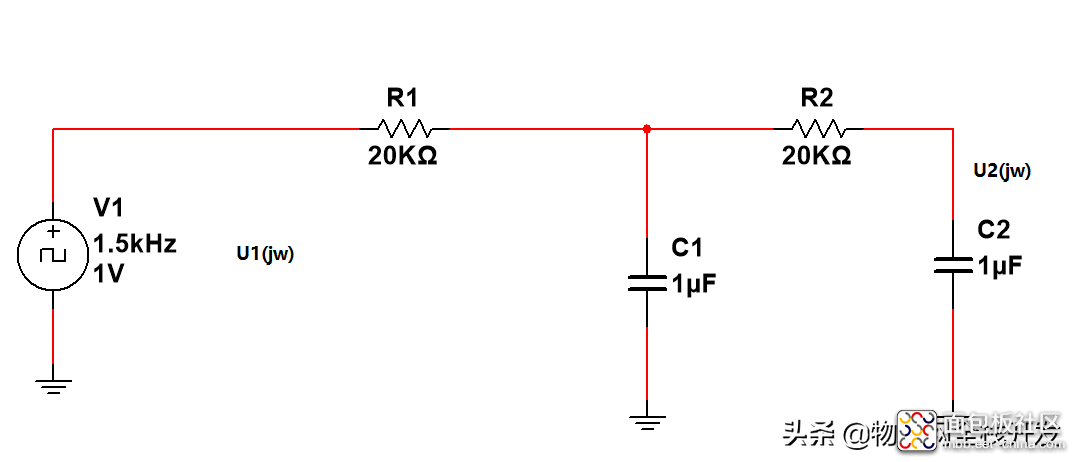
二阶R、C电路
对于二阶R、C电路,取R1=R2=R,C1=C2=C,其传递函数为:
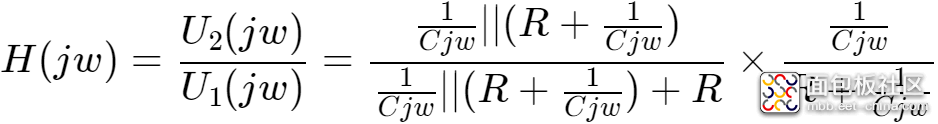
化简得下:

其幅度增益为:
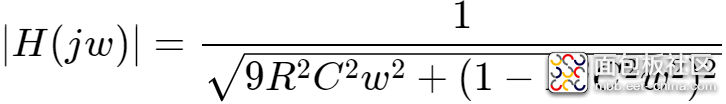
当R*C*w>>1时,
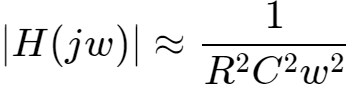
为了达到0.1%的精度,只需要:
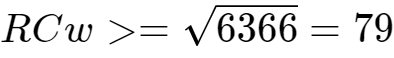
当PWM的频率为1.5KHz时,
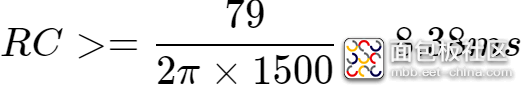
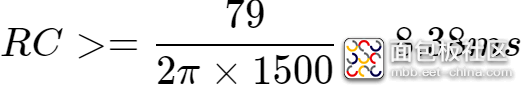
可以选择以下参数:
R1=R2=20kΩ,C1=C2=470nF。






 /4
/4 

