电子电路设计中，常用的滤波器分为高通滤波器、低通滤波器、带阻滤波器、带通滤波器，而这四种滤波器又统称为有源滤波器。下面单独谈一下这个低通滤波器的工作原理与运用。
低通滤波器特性：允许低频信号通过，将高频信号衰减。当信号处于低频段的时候幅频特性如下图所示：
6106ac7981a54e5086efc71779a54db1~noop.image?_iz=58558&from=article.jpg
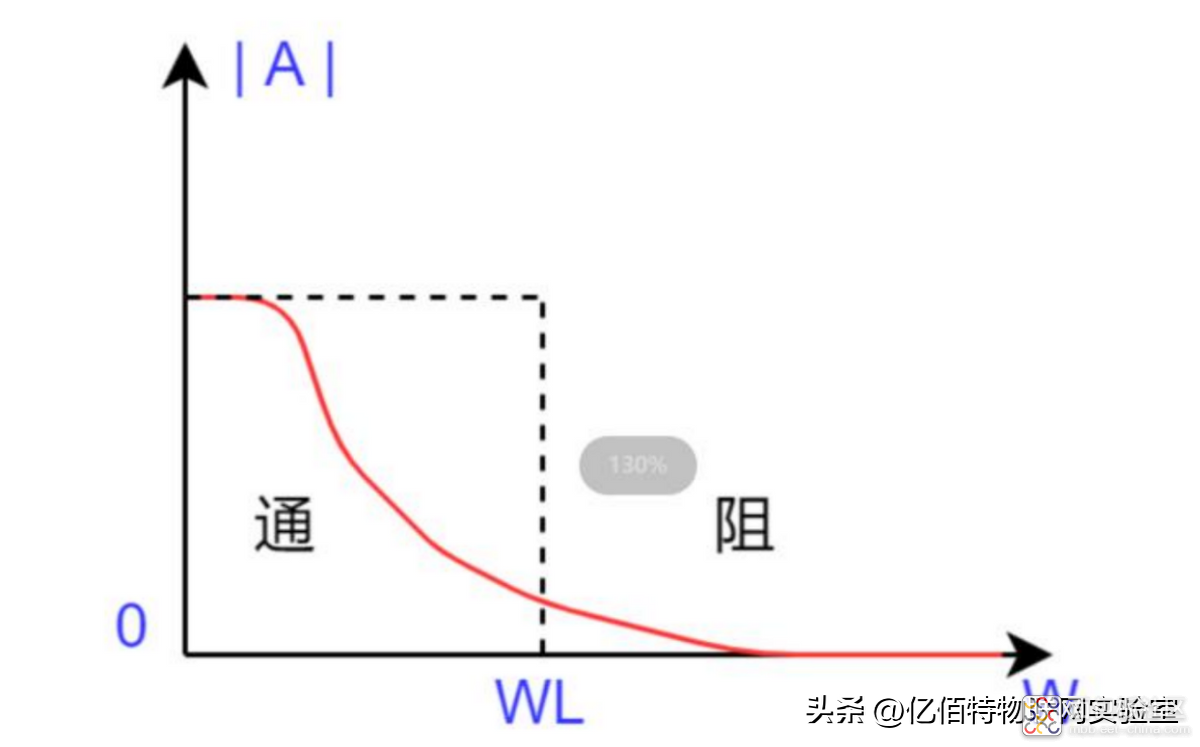
低通滤波器的原理解释完之后，再看下面的积分电路：
1eae2ec7596341549de426125ee8797d~noop.image?_iz=58558&from=article.jpg
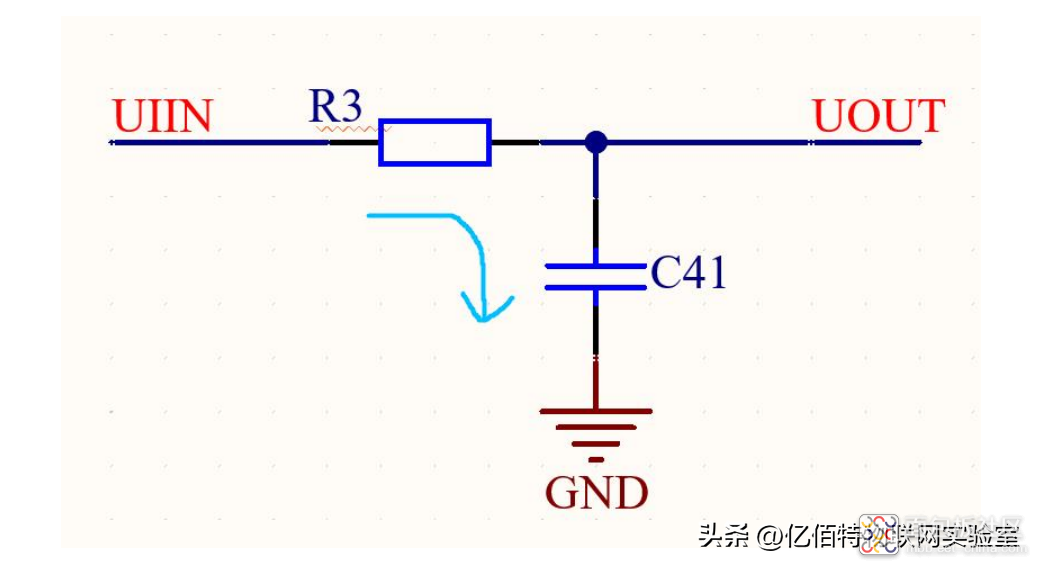
上图是简化电路之后的一个无源积分电路，简单分析这个积分电路，假设要求它的时间常数 T 需要大于它的信号脉冲宽度，而由于 T=RC，所以这个电路工作原理就是：
假设输入信号为矩形脉冲波（也可以是正弦波），当第一个脉冲波出现时，输入端产生一个电流，通过对 R3 和 C41 进行充电（电容两端的电压是不会突变的），这个时候，电容 C41 上的电压慢慢增加，当脉冲过去之后，输入端的信号 UIN 就会为 0（电容两端电压不会突变），所以时间常数 T 会比较大，相对地，它的放电就会变得很缓慢。
慢慢地，第二个脉冲又过来了，在这时，由于之前的电还是没有放掉，就可以知道，当输入脉冲波越密集，我们的 UOUT 就会越大。
总结一下来说，所谓的积分电路就是获取输入信号 UIN 的平均值形成的电路，换句话说也可以是低通滤波器电路。总结原理就是对低频段的信号进行采集采样，通过后面的电容存储，最后进行获取输入电流的平均值。下图可以形象描述：
9455b410c1824ddebd32c08a90c60be9~noop.image?_iz=58558&from=article.jpg
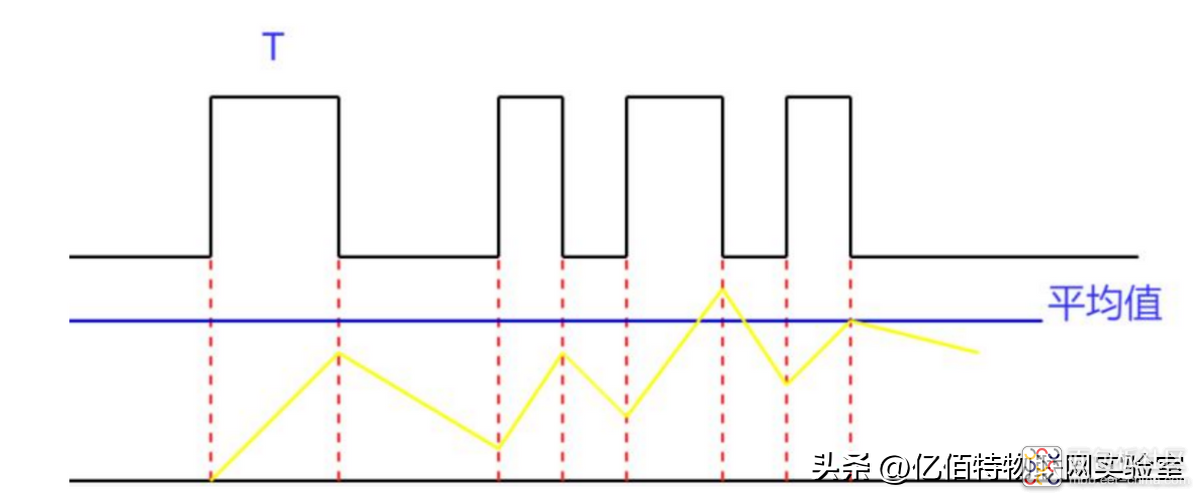
在弄清楚积分电路之后，再看低频滤波器电路就会一目了然，下面是小编绘制的两个低频滤波器电路：一阶低通滤波器、二阶低通滤波器。
fae6679be0434a009cd50327a4fbf7eb~noop.image?_iz=58558&from=article.jpg
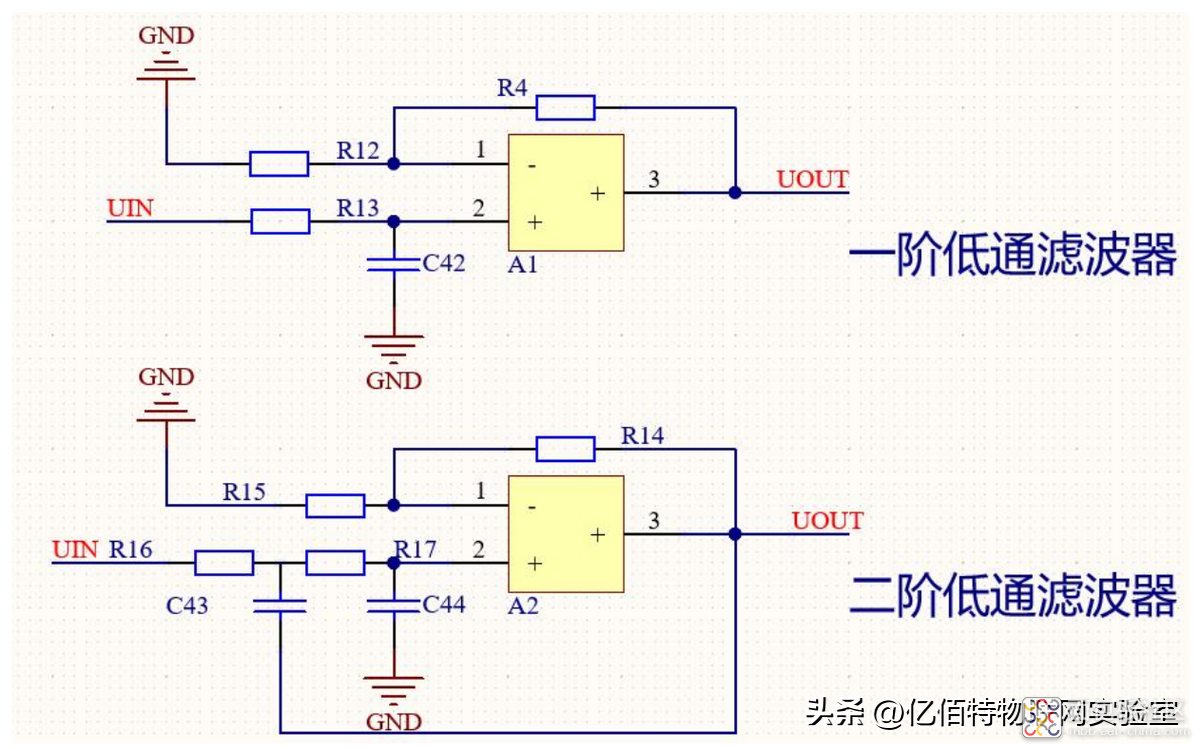
从图中，我们可以看到，两个滤波器都是由集成运放和无源低通滤波器组成（积分电路），而滤波器中反馈则是为了使运放工作在线性区域里面。分析这个一阶低通滤波器电路：
同比例运算电路（电压并联负反馈）由公式 AuP=（R4/R12）+1 计算放大倍数。
W=2πf=2π/t 计算角频率。
电阻和电容属于串联谐振，串联谐振频率就为：f0=1/（2πR13C42）。由于 PC 串联是只能用在交流回路上面进行分析的，而 RC 并联就可以用在交流和直流上。
平时电路设计中，常用的滤波器都是二阶和多阶，通过很多次的验证，都表明对于一阶滤波电路的滤波效果远远不如二阶滤波器电路效果，可以观察上面二阶滤波器原理图，有颗 C47 电容，它的作用是充当了一个正反馈的形式来改善截至频率附近的幅频效果。