几何傅里叶变换 |
时间:2020-09-29 13:02来源:讯技光电作者: 技术部点击:247次打印 |
Frank Wyrowski* and Christian Hellmann** *Applied Computational Optics Group, Institut fur Angewandte Physik, Friedrich-Schiller-Universitat Jena **Wyrowski Photonics UG mailto:frank.wyrowski@uni-jena.de 在系统的不同平面上,电磁场分量的傅里叶变换是连接空间域和k域的物理光学建模中的频繁操作。我们介绍一个场所谓的几何区域,在该区域中傅里叶变换可以在不进行积分的情况下得到,总之是以非常有效的数值方式得到。在几何场域中,场由波前相位控制,因此允许我们将稳定相位的概念应用于傅里叶变换积分,我们将所得到的傅里叶变换算法称为几何傅立叶变换,这项技术被证明是快速物理光学的基础支柱。 1.光学傅立叶变换 在物理光学中,我们处理电磁场的六个复数场分量(分别为E和H)。在空间域,他们表示为 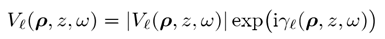
其中 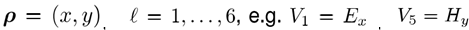
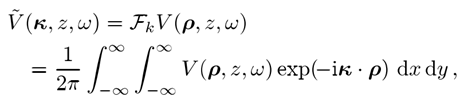
其中,我们使用符号 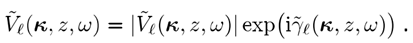
方程2中积分的数值评估需要对a和k域中的场进行取样,我们用N表示采样点的数量,所得的离散傅里叶变换构成了N2运算。然而快速傅里叶变换(FFT)算法在N中是线性的,这在原理上使快速物理光学建模成为可能,但FFT需要 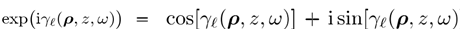
为了进一步研究,我们用波前相位Ψ将 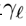
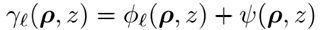
对于所有分量都是一样的。 显然,方程 4中的分解是模糊的,其依赖于从源场出发建模中恰当的相位处理方式。由定义 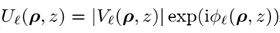
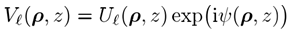
类似地,我们可以得到 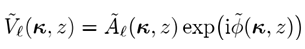
其中波前相位 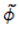
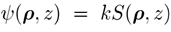
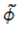
2 几何傅里叶变换理论 稳定相方法的应用在光学中是众所周知的,例如,用于讨论[2]中的衍射积分。我们将其用于快速计算方程2的傅里叶变换积分。为此,我们假设除临界点附近以外 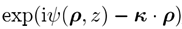
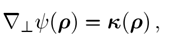
其中 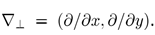
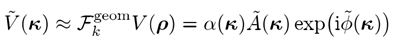
由φ(p)的勒让变换 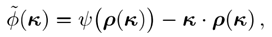
复函数 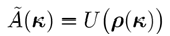
权重因子 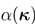
我们已经开发了一个数值算法来执行几何傅里叶变换。它利用场的混合采样。相比于函数 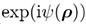
而且,我们必须用等距分布的采样点N(U)来处理函数U(p)的采样。一般来说,我们有 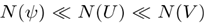
对于较弱的波前相位,半解析傅里叶变换也适用而快速[1]。连同数值上对于非常弱的波前相位有效的常规FFT,我们获得了一个强大的三元组来处理所有相关傅里叶变换的情况。它在VirtualLab Fusion的第二代技术更新中得以实现,构成了其快速物理光学技术的基础[3],例如古伊相移就是用这个概念来研究的[4]。 3 衍射、几何和远场区域 我们来考虑平面z中的一个场,它可以通过几何傅立叶变换以足够的精度(由质量标准来指定)进行变换。那么我们说该平面位于几何区域(GFZ),否则场在其衍射区(DFZ) 。自然地,衍射场区域位于焦点区域附近,而GFZ出现在距焦点区域较远处。如果场进一步传播,则可达到形成几何区域子集的远场区。在几何区域中,我们不限制波前相位 ,这意味着我们也包括像差。如果几何傅立叶变换为球面的 提供准确的结果,则已经达到远场区域,如表1中概括。对于一个衍射受限场,几何场和远场区是相同的,应该强调的是,在每个平面上,场的区域特征可以通过几何傅里叶变换来研究,这构成了一个纯粹的数学概念。事实证明,在场的几何区域中的物理光学建模可以很快地执行,因为数值上其主要涉及相对较小的波前相位样本数量 。 表1 场域的定义 
参考文献 [1] Z. Wang, S. Zhang, and F. Wyrowski, "The semi-analytical Fast Fouruer Transform," in Proc. DGaO, vol. 118, p. P2 (2017). [2] J. J. Stamnes, Waves in focal regions. Propagation, diffraction and focusing of light, sound and water waves (Adam Hilger, Bristol and Boston, 1986). [3] Fast physical optics software "Wyrowski VirtualLab Fusion", developed by Wyrowski Photonics UG, distributed by LightTrans GmbH, Jena, Germany. [4] O. Baladron-Zorita and F. Wyrowski, "The Role of the Gouy Phase Anomaly in the Unification of the Geometric and Physical Models for the Propagation of Focussed Fields, " in Proc. DGaO, vol. 118, p. P3 (2017). |





 /4
/4 

