
QPSK、8-PSK、16-QAM、32-QAM 和 64-QAM 制式的星座图
在模拟调制中,载波参量的改变是按连续的模拟信息。在数字调制中,这些载波参数(幅度,频率和相位)的变化由离散的数字信号决定。从这个意义上讲,数字调制和模拟调制并无本质区别。数字调制信号只须表示离散的调制状态,这些离散状态在矢量图上称为符号点 (symbol point),符号点的组合称为星座图(constellation)。
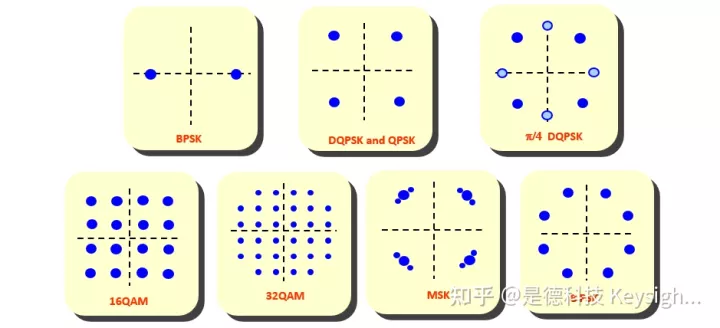
数字调制信号完成对时间离散状态的描述
星座图和符号
星座图展示了 QAM 格式的可用符号。以 16 QAM 格式为例,每个符号表示着四个二进制位的一种可能组合。对于这四个二进制位来说,总共可能有16个组合。换言之,每个符号表示着四位。
为了提高数据带宽,我们可以增加每个符号表示的位数,这样可以提高频谱效率。不过,随着星座图中符号数量的增加,符号间的距离开始变小。符号越来越接近,因此就越容易受到噪声和失真的影响,出现错误。下图展示了当从 16-QAM 格式变为 64-QAM 格式时,符号密度的增加。
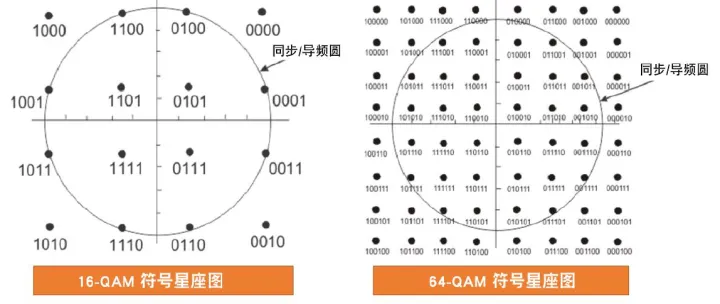
星座图和符号星座图展示了 QAM 格式的可用符号。16-QAM 和 64-QAM 格式的星座图
数字调制的基本术语
我们先来了解一些关键的术语。
比特 Bit :是通信系统传输信息的单位,一般指通信系统中传输的有用信息。
比特率 Bit Rate :是比特的传输速率,也就是通信系统时间内的信息传输速率,单位是比特/秒(bit/s)。
符号 Symbol :是信息调制载波的离散状态,也就是矢量,是与载波和调制方式紧密联系在一起的概念。模拟调制也可以说有符号,只是符号数量无穷多,无法直接分析和观察。因此只在数字调制中讨论符号,其符号数目是有限个。符号并不是信息,但信息是通过数字调制映射为载波状态即符号来传输的。
码元速率或符号率 Symbol Rate :载波调制符号的转换速率,实际上是载波状态的变化速率。符号率越高,相应信息传输速率也越高,但信号中包含的频谱成分也越高,占用频带越宽。单位是波特 (Baud)。
星座图 Constellation:调制信号在IQ平面上的所有符号点的组合。星座图定义调制技术的信号分布与调制数字比特之间的映射关系。一种调制技术的特性可由信号分布和映射完全定义,即可由星座图来完全定义。
矢量图 Vector Diagram:调制信号在符号点间变化的过程描述。矢量图不仅显示星座点,而且显示星座点之间的转换过程。
眼图 Eye Diagram:检查数字信号传输畸变的一种形象直观方法。它是解调后在低通滤波器输出未经再生的基带信号,在示波器上用位定时作为外同步时重复扫描显示的波形。
比特率与符号率(波特率)的关系
比特率是系统传输比特流的频率。符号率等于比特率除以每个符号可以传输的比特数。调制信号的矢量图
例如,在 QPSK 中,每个符号表示两个比特。QPSK 的符号率就是其比特率的一半。信号带宽和符号率成正比。
符号率=比特率/每个符号传输的比特数
我们讨论的调制信号都可以用正弦函数来表示:
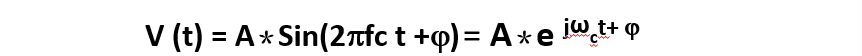
其中,A代表信号幅度,也是我们常说的信号电平。可以用不同的量度表征它,如功率,电压等。Sin括号内的是信号的瞬时相位,它分为两项,第一项是由载波频率fc决定的相位,是单位时间相位的变化;第二项是相对于零度的起始相位j 。所以频率实际是瞬时相位表达式的一部分,是相位变化的速度。
有两种不同于前面的矢量图表示方法:极坐标图和 I/Q直角坐标图。这两种表示方法都十分常用。
• 极坐标图表示的矢量的参数是幅度和瞬时相位,一般表示为AÐq
• 因为所有调制形式针对载波的改变都是幅度、相位以及可以由相位推导的频率。极坐标图是分析调制技术矢量参数的主要描述方式
• I/Q直角坐标图表示矢量的参数不是直接的幅度和瞬时相位,而是把它们投影在I/Q直角坐标轴上,采用 I 轴和Q轴的投影分量来确定矢量
- 使用 I/Q直角坐标图是因为和 I/Q调制的表示方法完全一样
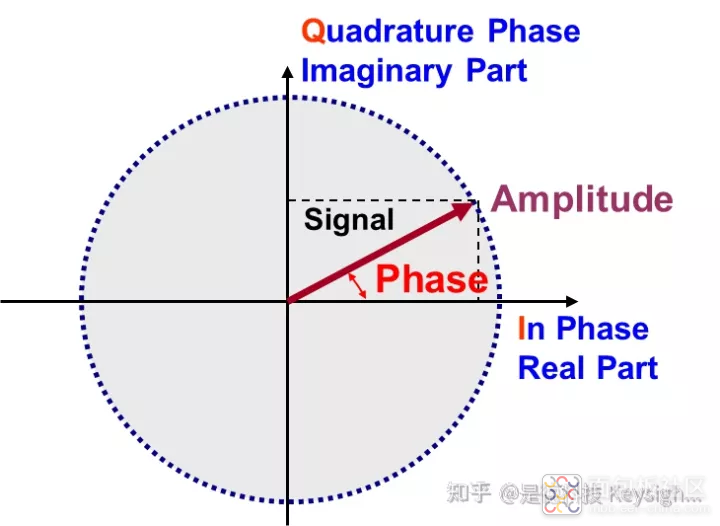
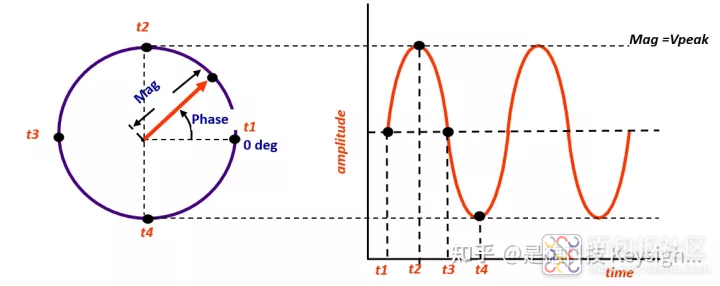
矢量的表示方法
用矢量来描述一个正弦波是非常方便的。在极坐标中,矢量表示正弦波的峰值电压幅度对于相位改变量的关系。相位旋转360度表示一个完整的频率周期。请注意,相向的符号提供了一种表示正弦波相位随时间变化的便捷方法。
幅度:是一个绝对值 相位:相对于一个参考值(载波)
l 幅度:是一个绝对值
l 相位:相对于一个参考值(载波)
图中正弦波表示了一种信号幅度随时间变化的过程。矢量不能直接提供任何频率信息。事实上,我们测量矢量相对于载波信号的参考相位。这意味着,矢量仅在频率不同时会发生旋转。
任何极坐标图中,如图沿径向的变化意味着信号幅度改变,如图角度的变化意味着信号相位改变(且仅仅是相位发生变化)。在极坐标中,可以观察各种信号:AM调制,PM调制,FM调制。记住,幅度和相位变化都是相对于未调制载波的。
传统的时域和频域可以直观的观察调制信号,但无法对调制参数进行深入的分析和测量,所以引入了矢量描述方法。
典型调制信号的矢量图描述
矢量图 (Vector diagram) 是描述矢量信号变化轨迹的一种直观方式:
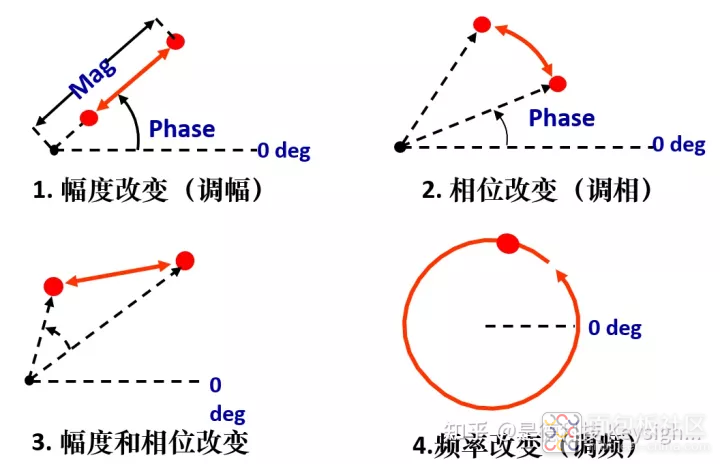
1 第一个实例是调幅(AM)波。因为调幅波的频率是不变的,射频频率与载频之间是固定不变的,仅相差一个初相角。看起来是一条从原点到某最大点之间的直线。其信号幅度则在两个圆点之间变化,其变化值与单位园半径之比就是信号的调幅指数。
2 第二个实例是调角波,包括调频波(FM)或调相波(PM)。因为调角波的信号幅度是固定不变的,仅在圆周上某个初相角处产生角度的变化。看起来就是在圆周上某一段弧线上变化。
3 实际上一个调幅信号的相位也不是绝对不变的,常伴随着小量不希望的相位变化,称为寄生调频或剩余调频(或调相)。一个调角信号的幅度也不是完全恒定的,因为调角信号中存在寄生调幅。结果在极坐标图中的信号轨迹如图三角形所示,它同时存在幅度与相位变化。
4 调幅或角系统产生的这种寄生调制,会使调制信号产生失真。调幅信号直线轨迹变成了折线或曲线。若在系统传递函数中存在滞后现象,则直线也可能变为环线状。总之,这些失真会导致解调信号的参数变化。
• 调幅或角系统产生的这种寄生调制,会使调制信号产生失真
• 如果频率不是一个恒定值,则转速也会变化

无线通信的调制技术和测试的发展
数字调制技术效率和抗干扰性的提高是实现高速无线数据传输的关键。近年来,主要发展趋势是数字调制,包括:QPSK(正交相移键控),FSK(频移键控)和MSK(最小频移键控),QAM(正交幅度调制)以及更加复杂、调制效率和抗干扰性更好的调制方式,如UWB中采用的正交频分复用技术OFDM (Orthogonal Frequency Division Modulation)。
全球范围内正在兴起数据中心的建设热潮,同时当今的CPU 和内存可以确保非常低的时延,能在几分之一秒内掌握大量数据在多台服务器上的分布信息。其他基础设施能否跟上这个步伐显得尤为重要。数据量的飞速增长已经变成了一个巨大的挑战。为了避免很快出现瓶颈,在数据旅程的每个阶段都需要提高比特率效率。
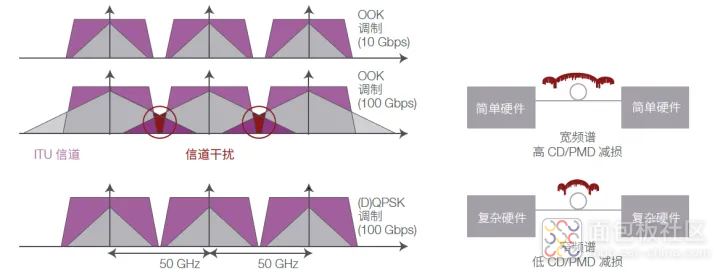
图 1. ITU 网格中的信号频谱。使用 OOK 时,信道干扰或衰减会在 100 Gbps 及以上速率造成严重的干扰,而复合调制方案可以解决这些问题
比特率与符号率(波特率)的关系
比特率是系统传输比特流的频率。符号率等于比特率除以每个符号可以传输的比特数。例如,在 QPSK 中,每个符号表示两个比特。QPSK 的符号率就是其比特率的一半。信号带宽和符号率成正比。
符号率=比特率/每个符号传输的比特数
您了解 OOK吗? - 掌握复合调制的优势
光数据传输最初就像电子数据传输一样,采用了最简单、因此成本也最低的数字编码方案:归零(RZ) 或非归零(NRZ) 开关键控(OOK)。信号是理想的1(通电)和0(断电)矩形序列。但是当传输速率达到40 Gbps 时,这一概念就会遇到限制。
由于40 和100 Gbps 的高时钟速率,OOK 信号所占用的带宽变得比50 GHz ITU 信道的带宽还大。如图1 所示,频谱扩大的信道开始与临近信道重叠,信号经过波长滤波器整形,结果会产生串扰和调制信息质量下降。
出于这个原因,高速传输需要从OOK 转向更复杂的调制方案,例如差分正交相移键控(DQPSK)。取决于符号时钟速率,复合调制可以减少需要的带宽,支持在50 GHz ITU信道规划中实现更高的数据传输速率。
这些概念还支持通过数字信号处理配合相干检测,对色散(CD) 和偏振模色散(PMD)进行补偿。
色散是什么意思?
色散是由于光波以不同速度进行传输(取决于光波频率和偏振状态)而产生的一种效应,它将会导致脉冲变宽,如果不进行补偿可能会降低信号质量。在长光纤中色散问题尤为严重。
复合调制方案使用光波的所有参数(幅度和频率或相位)进行信息编码,可以有效改善频谱效率。无线工程师多年来一直得益于这种方法,现在光通信工程师也能使用这种方法。
使用相干检测意味着,复合光调制不需要采用PMD 补偿器或色散补偿光纤,也不会遇到这些元件所增加的损耗和时延。
除了相干检测之外,复合调制方案还能与其他传输方法结合使用,通过光纤链路更高效地传送数据信号。例如,在偏振多路复用(PDM) 中,第二个光波信号与第一个光波信号正交偏振,可承载独立的信息,并通过同一条光纤进行传输(见图2)。这就像增加了另一个信道一样,无需使用第二条光纤便可将传输速度增加一倍。
图 2. 偏振多路复用
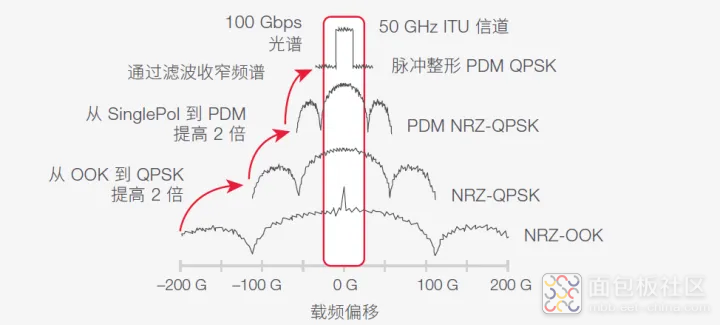
图 3. 使用复合调制、偏振复用和频谱整形可以提高 100 Gbps 数据信号的频谱效率。
图3 显示了这些不同技术的组合是如何改善频谱效率的。底部是最简单的方案:OOK。使用正交相移键控(QPSK) 的话,符号速率与OOK 相同,而传输速率可以增加一倍,这是因为在QPSK 中,一个符号可以编码2个比特。通过PDM 还可以使传输速率再增加一倍。
QPSK 加上PDM,可在相同时间内(即在相同时钟速率下)传送2 × 2 = 4 倍数量的比特。最后,使用脉冲成形滤波器可以进一步缩小所占用的频谱,在50 GHz 信道中可达到100 Gbps 的传输速率。
其他类型的多路复用(例如波分多路复用(WDM))技术仍在继续使用。脉冲成形滤波器(可减少信号占用的带宽)的使用,使工具箱得到了进一步的完善。
问题:难道对频谱效率没有更多限制吗?
上个世纪40 年代,美国数学家和电子工程师克劳德‧香农(信息理论之父)发现,在任何通信信道内,能够准确无误地传输数据的最大速度与噪声和带宽有关。他将这个最大比特率称为“信道容量”,也就是目前众所周知的“香农极限”。
香农-哈特利定理
信道容量:

其中 B 表示测得的带宽(Hz),S 表示接收的信号平均功率(W),N 表示平均噪声功率(W)。
信道容量可以通过增加带宽或优化信噪比(SNR = S/N) 来增加。
信道容量可以通过增加带宽或优化信噪比(SNR = S/N) 来增加。
实际上,该定理给出了理论上的最大值,但没有说明哪种信号概念可以让我们最接近这一极限。
SNR 是基本的限制因数。无论在现在还是未来,它都需要不断优化,因为当数据速率超过100 Gbps 时,远距离通信需要更好的信噪比性能才能在给定带宽内达到香农极限。
Ellis、Zhao 和Cotter 采用了实例参数来仿真与传输和检测类型有关的信息频谱密度C/B(图4)。对于非线性传输,信息频谱密度不会随着发射功率谱密度无限增长。由于功率放大器的饱和效应以及光纤本身的非线性效应,信息频谱密度有一个最大值。这与传输介质是完全线性时的情况不同。
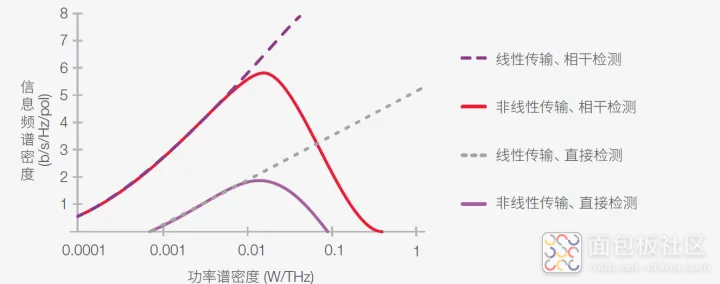
图 4. 与偏振有关的预期信息频谱密度限制示例。(A. D. Ellis、J. Zhao 和 D. Cotter,《接近非线性香农极限》,Journal of Lightwave Technology,第28 期,第4 号,2010 年2 月15 日)
此图清晰地说明,OOK 采用的直接检测只能从幅度提取信息,在信息频谱密度上无法与复合调制信号的相干检测相提并论。毫无疑问,不同类型的复合调制对您接近频谱效率香农极限的程度有着根本性的影响。
下面,我们首先来了解编码和调制方案的基础知识。
编码
提高光比特传输效率的复合编码概念
为了应对云革命和汹涌而来的数据浪潮,业界必须采用比开/关键控(OOK) 更高效的技术来通过现有光纤基础设施传输比特。例如,业界已经采用WDM 成功提高了单根光纤传输的比特数,同时也将把它用于复合调制信号传输。
现在,偏振多路复用(PDM) 可以让容量翻倍。除了WDM 和PDM 之外,通过复合调制还可以在一个信号状态(表示“符号”)内对多个比特进行编码。
复合传输在这一领域展现出巨大的潜力。复合传输不是发送二进制数据流,而是将多个比特编码成一个新符号,然后发送这些符号的数据流。图5 显示了2 个比特编码成1 个新符号的示例。通过这种方式,相同的带宽可以传输两倍的数据量。

图5. 编码概念:使用符号表示比特串,这里用一个字母符号表示2 个比特
当然,根据这一知识,我们可以想出多种方案,使用单个符号定义更多比特,使数据速率比仅能发送0 和1 数据串的OOK 高许多倍。
在实际中这是如何实现的?
在OOK 中,方法基本上是:当激光源开启时,表示“1”;当激光源关闭时,表示“0”。换句话说,当光幅度超过某个水平时,表示“1”;当光幅度低于这个水平时,表示“0”。不过,由于光波不仅仅是由幅度一个参数所定义,因此我们还可以采用其他方法,利用光波的各种自由度来对信息进行编码。
图6 所示为电磁波的电场数学描述,电磁波中包含两个偏振分量Ex 和Ey。这些正交分量在PDM 中用作两个不同的信道来发送独立信号。在WDM 中,不同的频率ω 用作不同信道,在这些频率/波长上进行独立的数据传送。现在对于复合调制方案来说,除了幅度E 之外,光波的相位Ф 也可以经过调制用于定义上述符号。

图6. 电磁波(电场)的数学描述
调制光波的电场也可以用I/Q 图中的复数平面来描述。这里,I 是同相或实部,Q 是正交或虚部,如图7 所示(在去除了波的时间和空间依赖性之后,仅用于一个偏振面)。符号对应于图(也称为“星座图”)上的一个点(也称为“星座点”),由极坐标中的I 和Q 值通过幅度E 和相位φ 定义。星座点对应的是符号时钟时间,也称为“检测决策点”。
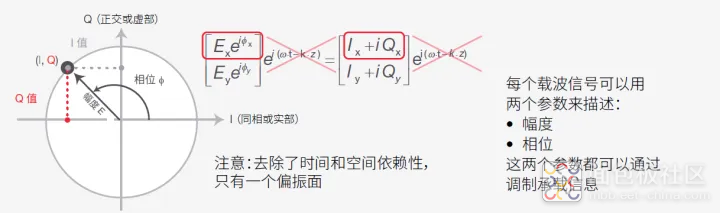
图7. 符号的I/Q 表示
有 4 个可能的矢量。
复数平面中的一个矢量位置对 2 个比特进行编码
复数平面中的一个矢量位置对 2 个比特进行编码
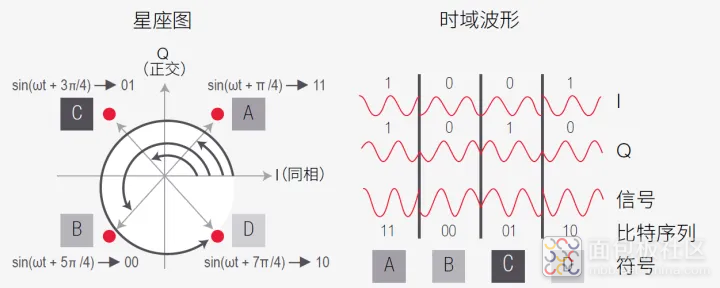
图8. 4 个符号/星座点,一个符号编码 2 个比特(正交相移键控(QPSK))
图8 显示了正交相移键控(QPSK) 中的4 个符号的星座点。QPSK 是一种复合调制类型,使用4 个符号对每2 个比特进行编码。星座点位于半径为E 的圆上。这意味着符号只是相位不同(相邻两点的相位差大约为π/2),幅度是相同的。在时域中,4 个符号可使用幅度相同、相位不同的两个波形的组合来表示。
传统的OOK 也可用星座图表示。由于信息只能通过幅度来编码,所以比特值1 可能在半径(= 幅度)为E 的圆上的任意点(见图9)。
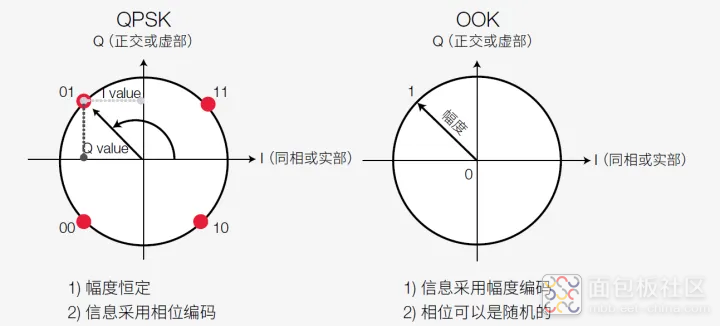
图9. QPSK 调制与 OOK 的星座图比较;在 OOK 中,相位是随机的。
下面我们将介绍几种调制方案并加以对比,帮助您选择最适当的方案。
我们现在实际上使用两种不同的速度。第一种是以每秒比特数为单位的比特率 ftx,也称 为“传输速率”。第二种是符号率 S,表示每秒传输的符号数,单位为波特。它也因此通 常被称为“波特率”。
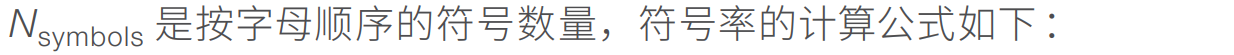
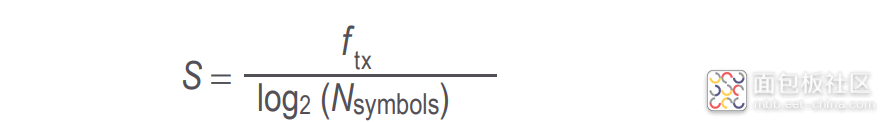
图 10 是 QPSK 公式。 如果信号也被偏振复用,那么这个结果要除以 2。以一个 100-Gbps QPSK 信号为例,符号率 S = (100 Gbps) / (2 比特/符号 ) / ( 2 偏振 ) = 25 Gbaud。最低光占 用带宽是 25 GHz。
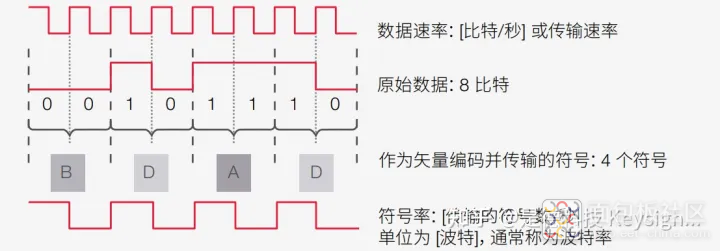
图 10. QPSK 的符号率与数据速率
因此,复合调制信号所需的带宽并不取决于数据速率,而是只与符号率有关。这也意味着, 以给定 数 据 速率编入单个符号中的比特数目越多,光占用带宽 就会 越 小。换句话 说, 当符号速率不变时,可以通过增加每个符号的比特数同时保持占用的光学带宽来提高数 据速率(图 11)。这项技术通常用于提高频谱效率。
所需光带宽
图 11. 通过增加单个符号中被编入的比特数,可以提高数据速率。符号率是恒定值,所需的光带宽保持不变。 从狭义上讲,在任何情况下,在单个符号中编入更多比特的调制方案都会是正确选择。 除了占用带宽以外, 还 应考虑适用范围、 技术可行性、 现有基础设施等。 现代 DSP ASICS 通常通过可配置的调制制式来支持不同的数据速率,每个符号具有不同的比特数, 并针对各自的吞吐量和覆盖要求优化频谱效率。
相移键控方案
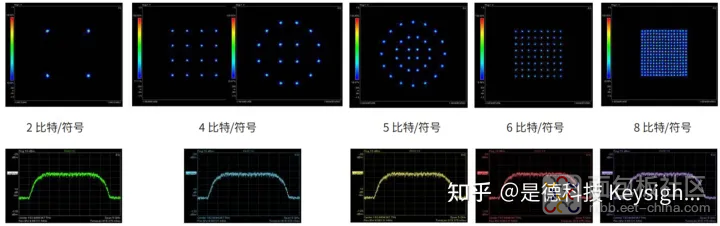
相移键控方案的幅度是恒定的,只需关注相位信息。像 WDM 和偏振多路复用 (PDM) 这 样的传统技术始终可与任意相移键控编码方案配合使用,以获得额外的数据传输能力。 多路复用技术定义了用于传输不同的相位调制信号的多个信道(图 12)。
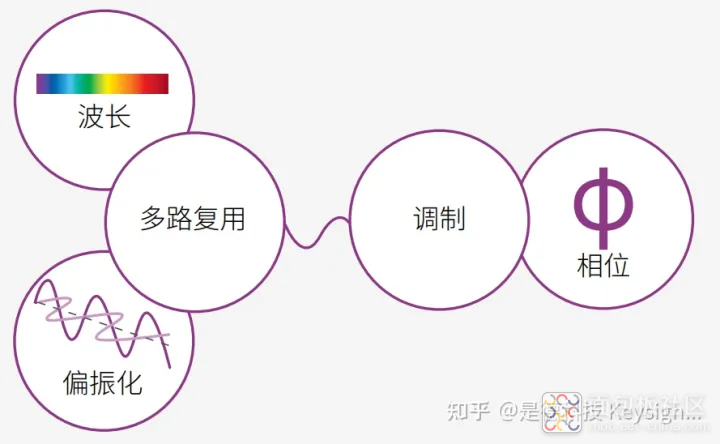
图 12. 获得数据传输能力的不同方式
什么是BPSK(二进制相移键控)?
二进制相移键控 (BPSK) 是最简单的一种相移键控制式。它具有两个相隔 180o 的相位值,例如:0 和 π(参见图 13)。幅度是恒定的。与启闭键控 (OOK) 相比,这两个 符号的间距很大,可免受失真和噪声的干扰。因此,BPSK 非常适合超长距离应用,例 如数据速率为 40 Gbps 的海底光纤网络。
BPSK 时域波形

图 13. BPSK 二进制相移键控
BPSK 的不足之处是每个符号仅表示 1 比 特, 这一点与 OOK 相同, 因此不适合用于 100 Gbps 及数据速率更高的应用。BPSK 相对于 OOK 的劣势是它很难确定信号的绝对相位。需要采用更复杂、更昂贵的方法 ;相干检测是关键。对于 OOK,光电二极管可以 检测出承载信息的幅度。这也称为“直接检测”。
差分相移键控 (DPSK)
为了避免进行相干检测,需要对 BPSK 进行修改。对于 DPSK 信号, π 的相位变化表示 0,而不是绝对相位 π。如果从一个比特到下一个比特的相位没有发生 改变,可以称之为 1。在接收机一侧,数据流被分成两个相同的流,两个流之间有一个 比特周期的时延。将两个数据流混合在一起(参见图 14),就能生成一个信号,光电探测 器可以直接检测到该信号。这种混合信号的强度更高。
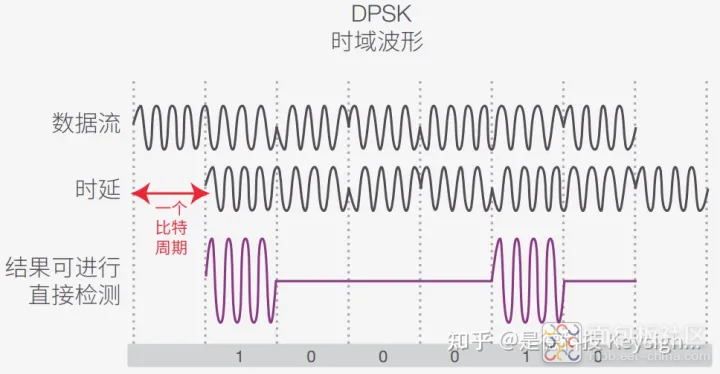
图 14. DPSK 信号可直接进行检测
与 OOK 类似,DPSK 每个符号中仅有 1 比特,因而不适合数据速率极高的应用。但对于 数据速率为 40Gbps 的长距离和超长距离应用,DPSK 不失为一种良好选择。
四相相移键控 (QPSK)
在前面中我们讲到,QPSK 的 1 个符号表示 2 个比特。4 个星 座点的相位相差 π/2,而幅度是恒定值(参见图 8)。相对于 OOK 和 BPSK,QPSK 可在 带宽不变的情况下让数据速率翻倍,这意味着,它也能够在一半带宽上提供原有的数据 速率。QPSK 通常用于 100 Gbps 的数据速率。信号相位检测要求使用相干技术。
差分正交相移键控 (DPSK)
为避免接收机端上的 QPSK 出现由光纤引起的相移所造成 的相位模糊现象,正如 BPSK 一样,可采用另一种 QPSK 制式 :DQPSK。使用已传输符 号间的相移来表示信息。4 个可能的相移值通常为:0、-π/2、π/2 或 π。 与 OOK 和 BPSK 相比,在保持带宽不变的同时,数据速率可以翻倍。或者说,它能以一半 的带宽保持相同的数据速率。
DQPSK 的 BER 低于 QPSK,但对离差 (dispersion) 的容限程度不高。
与 OOK 和 DPSK 类似, DQPSK 信号可被直接检测。
幅移键控和相移键控方案
在幅移键控和相移键控方案中,信息同时在相位和幅度中编码。传统技术(例如多路复用) 可用于进一步增加单位时间内传输的数据量(图 15)。
图 15. 具有多路复用的振幅相位调制方案
正交幅度调制 (QAM)
使用 QAM 调制方案可以让数据速率达到 400 Gbps 或更高。QAM 信号的调制和解调更加复杂,要比其他制式的成本要高。换句话说,高阶 QAM 的星座点比纯粹 PSK(例如 BPSK 或 8-PSK)更加分散。它们不容易受到噪声和失真的影响,BER 也会降低。
在 2n -QAM 方案中,2n 星座点表示每个符号有一组 n 比特,通常分布在正方形点阵(参 见图 16)。2-QAM(最低阶 QAM)每符号仅有 1 比特。在对应 1 和 0 的两个星座点之间, 幅度保持不变,但存在 π 的相位差。因此,2-QAM 实际上与 BPSK 是同一个方案。同样地, 4-QAM 从概念上讲不同于 QPSK,但两者的星座图是一样的。同样,这里只有 1个幅度值, 4 个星座点之间的相位差为 π/2。8-QAM 可能有 2 个幅度值和 4 个相差 π/2 的相位值,它们 定义了星座点,每个点表示 3 个比特。
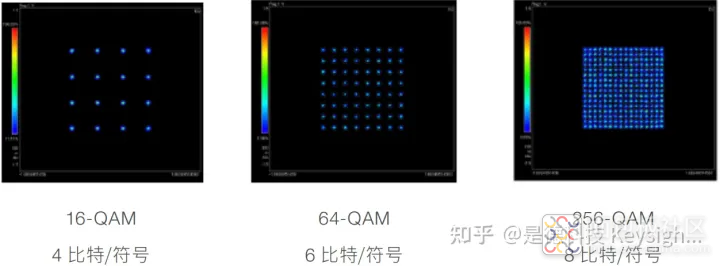
图 16.QAM 方案的星座点以正方形点阵分布
在其他的 2n -QAM 方案(n 是奇数)中,很难使星座点呈现正方形点阵分布(与图 17 对比)。 这会对 BER 性能带来负面影响 ;实际上,8-QAM 方案并不实用。相反,16-QAM 的频谱 效率是 8-QAM 的两倍,且 BER 的增幅很小,因而更受欢迎。
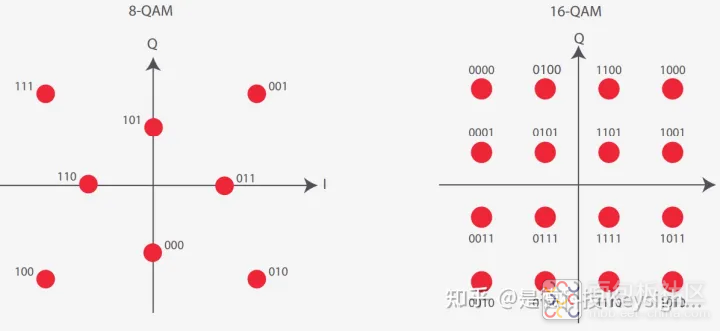
图 17. 8-QAM 星座图 图 18. 16-QAM 星座图
16-QAM
每个符号表示 4 比特。16 个星座点呈现正方形点阵分布(参见图 18)。它们通 常是格雷码,相邻两个星座点之间的变化只有 1 比特。由于噪声的影响,某个已测点被错 误地分配给邻近点,比特误码率保持在最低:1 个错误比特。
幅移键控和相移键控
在 APSK 中,一如其名,幅度和相位均被调制。与 QAM 不同的是, 它的星座点分布在 I/Q 平面中的同心圆上。 这个概念被引入到卫星系统(射频功率放大器具有非线性特性)。因此需要一个能够容忍 非线性放大的调制方案(包含较少的幅度),以便更轻松地平衡这种非线性。
图 19 对比了16-QAM 和 16-APSK 的星座图,其中 16-QAM 有 3 个幅度,而 16-APSK 只 有 2 个。32-QAM 有 5 个幅度,而 32-APSK 有 3 个。注意:QAM 振铃的间距是不均匀的, 有的振铃间距很窄,从而加剧了非线性补偿的难度。
在光纤中,APSK 可应用到非线性噪声场景中,用于改善对非线性光纤特征的容忍度。当 数据速率高达 400 Gbps 及以上时,16-QAM 的星座点间距较大,更易实施且光信噪比性 能更佳,因而是首选的方案。
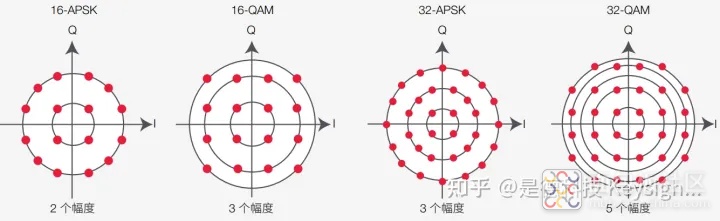
图 19. APSK 方案的星座图和对应的 QAM 制式
码间干扰 (ISI)
为了更高效地使用现有的有限带宽资源,我们必须认识到,复合调制信号在时域中扩展,连续符号可能会重叠,这种情况被称为码间干扰 (ISI)。ISI 会导致接收机对信号的解读出错。在频域中,我们也同样需要注意避免相邻信道之间出现干扰。数据速率达到400 Gbps 和 1 Tbps 时,干扰问题将变得极其重要。
我们将详细介绍了消除干扰效应所需的各种条件,并描述了用于带宽和信号隔离的不同滤波技术。
奈奎斯特码间干扰 ISI 准则
瑞典工程师 Harry Nyquist 在 20 世纪 20 年代曾经说过,为了消除 ISI,脉冲响应 h(t) 需要在时域中满足以下要求:( H. Nyquist:《电报传输理论中的几个主题》,Trans. AIEE,第 47 期,第 617-644 页,1928 年 4 月)
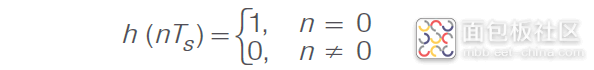
对于所有整数n ,TS 是相邻脉冲的脉冲间隔。
图 20 中使用了一个满足 sinc (t) 脉冲条件的信号来阐述这一准则带来的影响:脉冲重叠,但只有经过采样的符号会对采样时刻 tk 造成响应。其他的符号此时为零。通过这种方式,我们避免了 ISI 效应带来的信号衰减和误码。
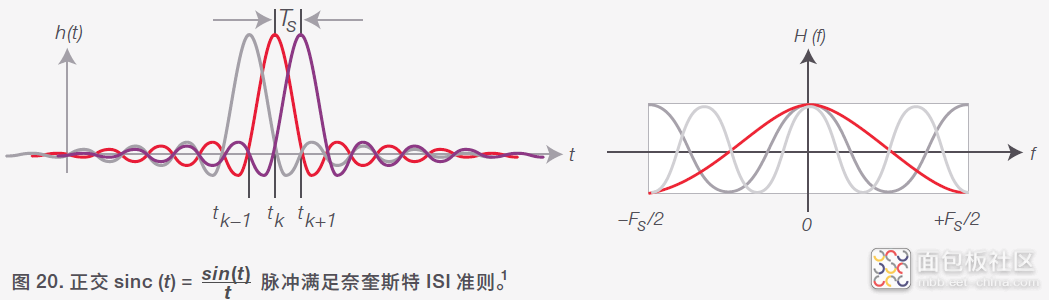
图 20 右侧显示了脉冲响应的傅立叶变换 (FT)。可以看出,矩形频率窗口内的频率响应能够满足奈奎斯特 ISI 准则 :
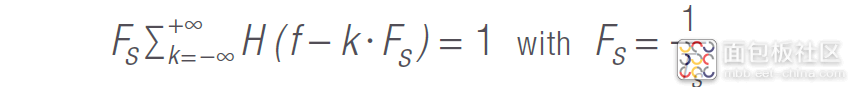
这意味着,谐波(频率为奈奎斯特频率 FS 整数倍的分量)必须加总为一个恒定值,以适应无 ISI 的频段。奈奎斯特频率 FS 是在不丢失信息的前提下对信号进行编码所需的最小带宽。
使用有限脉冲响应滤波器的奈奎斯特脉冲整形
如上所述,sinc 信号非常适合用于预防 ISI,但它不实用,因为它会在时间上无限延长。为此,我们需要使用有限脉冲响应 (FIR) 滤波器在时域中截取这个信号。一个阶数为 R 的 FIR 滤波器对应着 R+1 采样点,随后归零。滤波器输出 y[n] 的卷积仅考虑过去的采样点 x[n-i],因此可以实时进行过滤。
离散时间 FIR 滤波器的输出 y[n] 与输入 x[n] 有关系,如下所示 :
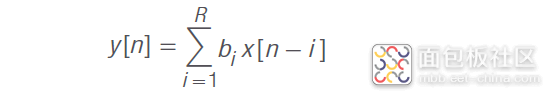
其中,bi 是滤波器系数。
为避免产生混叠,脉冲整形 FIR 滤波器必须至少按 q = 2 的系数进行过采样。换言之,在 TS 内必须至少有 1 个采样点。由此,脉冲形状可在接收机端重建,且不会丢失高频分量。
图 21 所示为以不同滤波器阶数 R 滤波的 sinc 脉冲的滤波器结果,始终以 q = 2 的系数进行过采样。功率谱是由正弦脉冲的矩形频谱与矩形窗口的正弦形光谱的卷积产生。
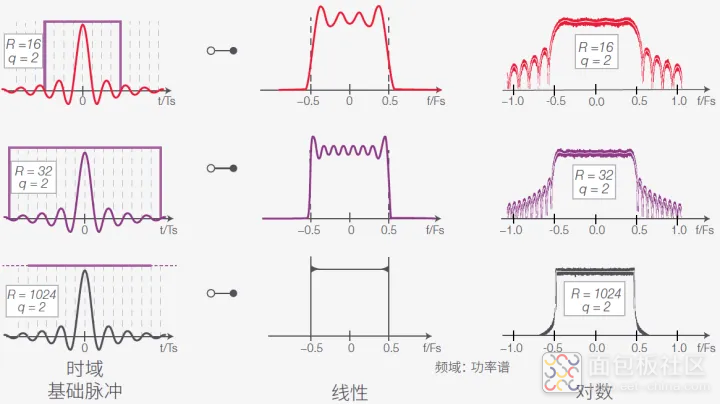
图 21. 使用不同阶数 R 的 FIR 滤波器截取 sinc 信号:在对采用线性和对数标度的功率谱进行快速傅立叶变换之后的时域波形 (R. Schmogrow M. Winter,M. Meyer, D. Hillerkuss,S. Wolf, B. Baeuerle,A. Ludwig,B. Nebendahl, S. Ben-Ezra,J. Meyer,M. Dreschmann,M. Huebner,J. Becker,C. Koos,W. Freude 和 J. Leuthold : 《超过 100 Gb/s 的实时奈奎斯特脉冲生成及其与 OFDM 的关系》,Optics Express,第 20 (1) 期, 第 317 – 337 页,2012 年 1 月)
第一行中,滤波器阶数为 16,信号跨越了 8 TS。在 FFT 中,可以看到有限时间窗口产生了失真。大部分功率位于奈奎斯特频段 (-0.5 FS 至 0.5 FS),但有一部分位于频段外。 功率谱以图谱形式显示谐波。
假设滤波器的长度增加一倍 (R = 32),信号能够更好地适应带宽,但会出现振铃。当 R = 1024 时,频谱几近完美;振铃仅在陡峭边沿上可见,功率谱还显示出较少的带外成分。遗憾的是,滤波器的阶数 R 越高,滤波器设计的复杂程度也就越高。因此,通常希望采用满足要求的最低阶 R。
升余弦滤波器的概念
为了获得更好的带外抑制和无振铃频谱,升余弦滤波器是合适的备选方案。脉冲响应取决于滚降因数α(0 至 1 之间的任意值):
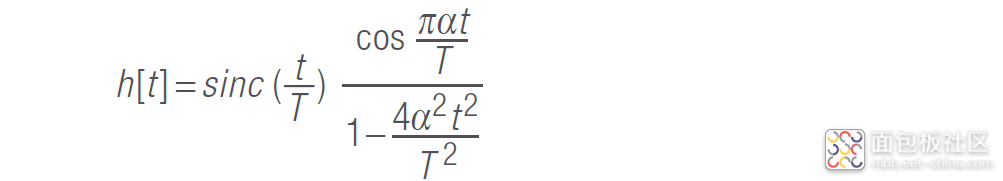
升余弦滤波器也能满足奈奎斯特 ISI 准则,即,只有经采样的符号会对信号造成响应。 在采样点上的其他符号均为零。与 sinc 整形脉冲相比,升余弦信号要求更多的带宽。
图 22 描述了4 个不同滚降系数α 的滤波器响应:
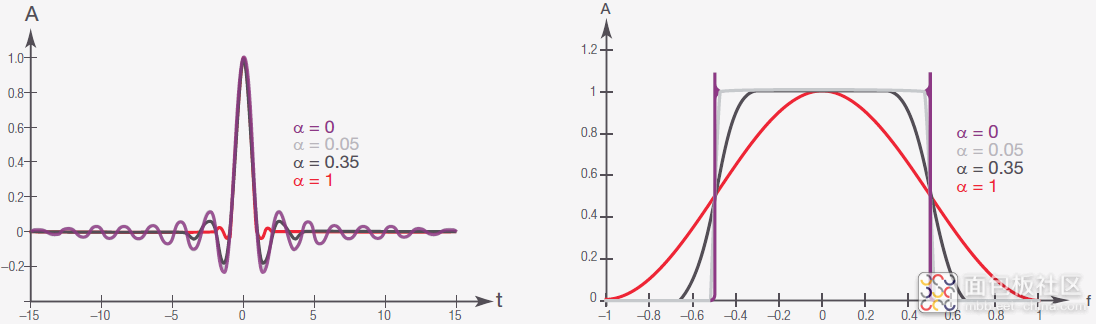
图 22. 具有不同滚降系数的升余弦滤波器 :归一化时域和频域呈现
在频率响应中它表示,对于任何 α 值,曲线在 ±FS /2 的同一点上交叉,这是脉冲速率的一半。如前所述,这个是奈奎斯特频率——在不丢失信息的前提下进行数据传输所需的最小带宽。除此之外,当α = 1 时,几乎没有振铃,但频谱不会适应带宽。
当α = 0 时,情况正好相反:频率响应在带宽范围内为矩形(边沿上的过冲仅仅是数学效应,也称之为吉伯斯现象,没有任何实际影响)。然而,时域信号显示出更多振铃。
在采样点上,只有经过采样的符号会对信号造成响应,但为什么振铃会是问题?实际上, 当我们只在理想瞬间采样时,其他的符号均为零,因此振铃成为问题。在实际条件下,接收机几乎不可能在这个点上进行精确采样,因此在信号解读时始终会有部分 ISI 产生误差。
很明显,时域中的带宽限制和振铃抑制之间需要进行权衡。对于每一个光纤应用,在选择足够的 α 值时都要加以权衡。
实际应用中的升余弦滤波器
我们仔细来看一下不同滚降系数对最有希望的 400 Gbps 调制方案的影响:16-QAM。 图23 显示了频域响应测量、眼图测量、以及对星座点之间转换产生的影响。
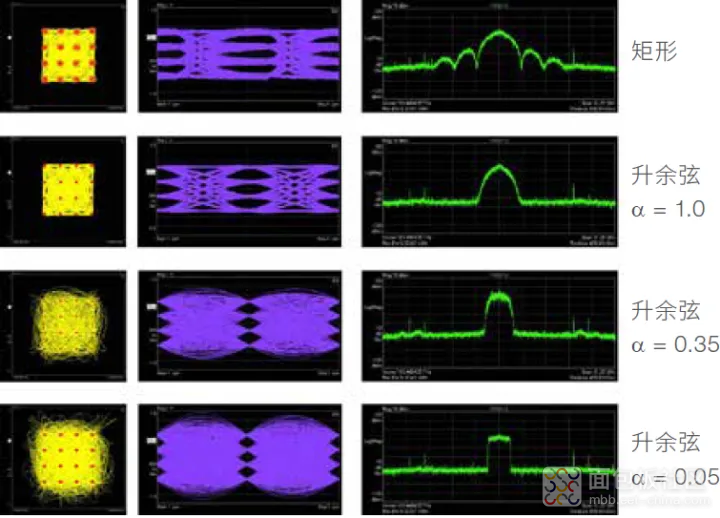
图 23. 16-QAM 信号上的升余弦滤波器与滚降因数的关系 :星座图、眼图和频谱 ;使用 Keysight M8190A 任意波形发生器创建的信号。
上例显示了无定形的矩形脉冲。已知只占据固定时间间隔的信号具有无限扩展的频谱; 在频率响应中可以看到大的旁瓣。眼图显示了开眼的宽带信号的典型特性。在星座点之间存在直接转换。
使用滚降系数α = 1 的升余弦滤波器,频谱会变狭窄 ;不会再看到旁瓣。在眼图中,眼图张开度很大。星座点较小。这是带宽较窄的系统的典型特征。接收机端的检测带宽也会降低,由此减少了噪声。
当滚降系数α = 0.35 时,频宽进一步减少,星座点的大小也随之降低。星座点的转换开始显示很多过冲。这是因为当带宽降低时,符号间的跳变时间就会延长,体现在星座图中就是星座点之间存在很长的跳变曲线。眼图闭合,采样时间变得更加重要。
在α = 0.05 时可以得到几近完美的矩形频谱。星座点之间的跳变显示了较大的过冲。完全 闭合的眼图表明,采样点必须经过精确调整,以免产生误差。
我们能够获得怎样的频谱效率?
为了解脉冲整形滤波器带来的频谱效率提升,我们将其与应用正交频分复用 (OFDM) 所产生的效应进行比较。图 24 简单描述了OFDM原理,与奈奎斯特制式类似。
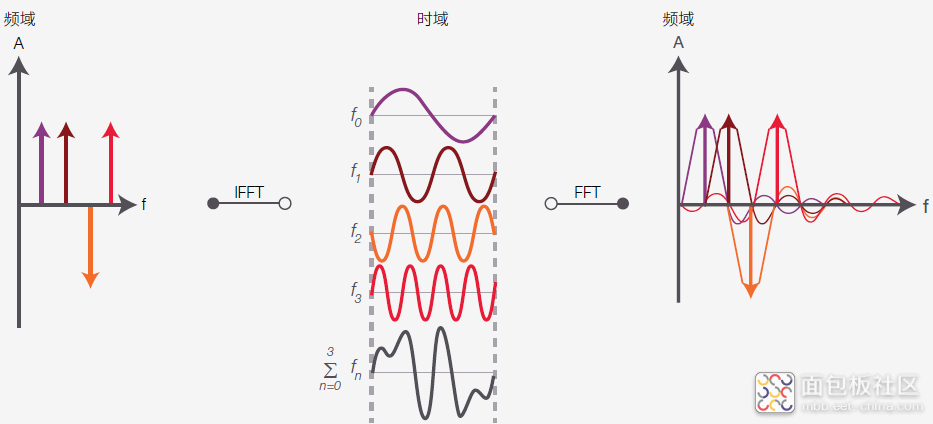
图 24. 频域和时域中的 OFDM
在 OFDM 中,频率子频谱是 sinc 形状。为了提高频谱效率,子频谱会重叠,但由于它们存在正交性(以 π/2 的倍数位移),因此它们彼此间不会形成干扰。在时域中,符号是在固定的时间窗口中具有等距载频 fn 的正弦曲线的总和。在本例中,单个信道的 4 个频率上有 4 个子载波。在进行反向快速傅立叶变换 (IFFT) 之后,橘色迹线相移了π。
图 25 显示了对 16-QAM 调制 OFDM 信号进行频谱分析。
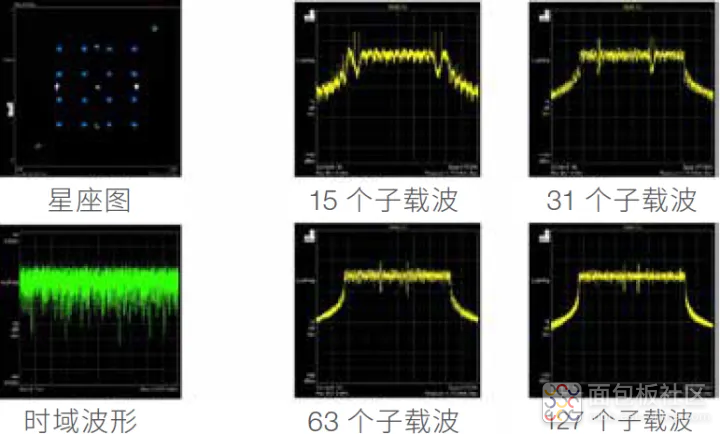
图 25. OFDM 对 16-QAM 信号频谱的影响取决于子载波的数目;使用 Keysight M8190A 任意波形发生器 生成的信号
左上角是星座图和时域波形。图中有 15 个子载波和 2 个导频,我们可以看到相对平坦的频率频谱和急剧的滚降。
通过增加子载波的数目,频谱变得扁平,2 个导频向中心移动。在基线上,可以看到频谱随着子载波数目的增加而趋向于矩形。
与奈奎斯特脉冲整形相比,它是如何提高频谱效率的?在图 26 中,在奈奎斯特滤波器长度R(过采样系数 q 选定为 2)上绘制了归一化的频谱效率 (SE),与 OFDM 子载波数目 N 进行比较。
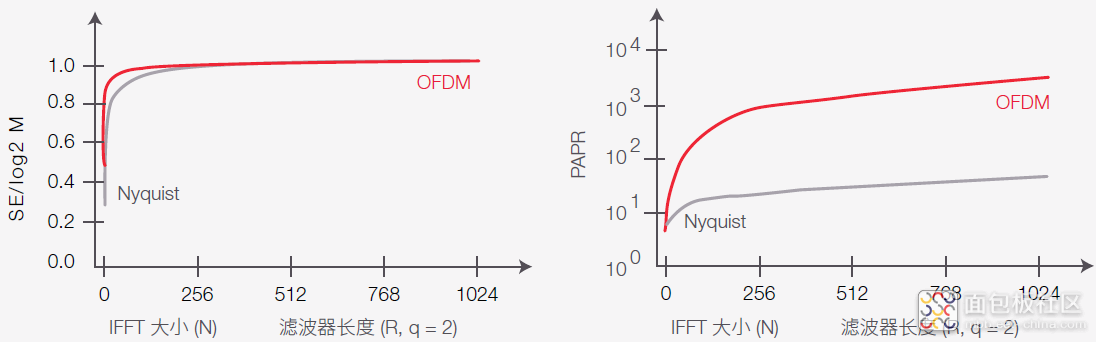
图 26. 奈奎斯特脉冲整形与 OFDM 对频谱效率和峰均功率比 (PAPR) 的影响
图中显示了两种技术提供近似的频谱效率。
归一化峰均功率比 (PAPR) 的对比揭示了两者在不同程度上具有类似的特性。OFDM 时域波形的 PAPR 更高。出现这种现象的原因是,在 OFDM 中,信号会呈现出高于平均功率值的一些峰值。由此,OFDM 电路和测试仪器需要较高的动态范围,以避免因限制较高的功率电平而引起失真。
迄今为止,我们已经反复提到了进行更复杂的数据传输需满足的技术要求。
下面我们将详细研究复合调制给光发射机技术实施带来的挑战- 满足各种需求的光发射机
在只考虑光幅度作为信息载体的 OOK 中,通过使用光波的相位来编码数据,可以实现新的可能性, 这种方法也会带来一定的技术挑战。
在传输 OOK 信号时,只需要由电信号直接调制的激光源即可。得到的光信号具有二进制强度。但如果需要对相位进行调制,这类简洁的低成本方法则很难实现。
利用电光效应控制光信号相位
好消息是,尽管发射机的复杂程度日益增加,但我们无需担心网络传输的色散补偿问题。接收端的信号处理算法可以管理色散损耗,因此不再需要色散补偿模块,新建光网络的成本也随之显著降低。
构建相位调制器时,我们可以借助特定晶体(例如铌酸锂)的折射率n 受局域电场强度影响的“电光效应”。这种现象被称为“电光效应”。
这种效应对相位调制有何帮助?假设 n 与场强有关系,那么光在晶体内的传播速度和波长也与场强有关系。因此,如果向晶体应用电压,那么穿过晶体的光波长减小,并且可以通过选择适当的电压来控制出射光的相位(参见图 27)。
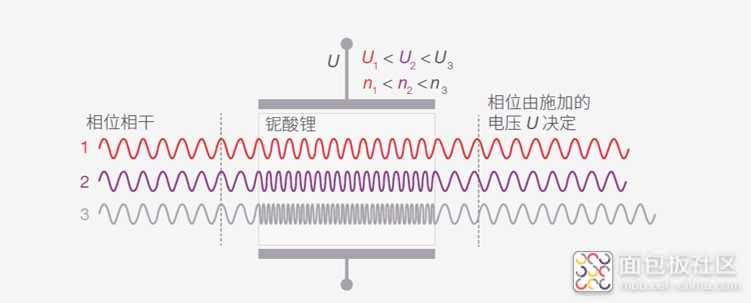
图 27. 施加的电压 U 越高,光在晶体内的传播速度就越慢。这种现象可用于控制输出光的相位。
Mach-Zehnder 调制器就是电光效应的一个应用实例。将一个光束一分为二,其中一束或两束经过类似上述的相移铌酸锂元件完成相位调制。两个信号之间存在相位差 ΔΦ,该值取决于两个信号路径之间的电压差 ΔU。因此,两个调制信号重新组合时,ΔU 也可以确定信号是相长干涉或者相消干涉。
图 28 的方框图显示了发射光功率与 ΔU 之间的周期关系。半波电压 Uπ 是完成功率传输相变 π 需要的电压,表示调制器 0 功率和 100% 输入功率传输之间的电压差。
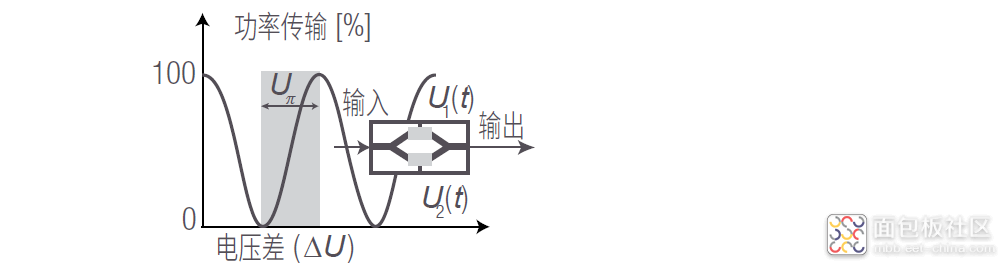
图 28. Mach-Zehnder 调制器发射功率与电压差之间的周期关系,其中 Uπ 是 0 与 100% 功率传输之间的电压差。
Mach-Zehnder 调制器的相移效应也可以使用 IQ 图来描述。图 29 是一个正弦波示例,具有恒定的幅度,相对相位 Φ = 0。在信号分离之后,每个分支上只有一半的功率。 在紫色示例中,调制器支路没有施加任何电压,因此两个支路(假设长度相等)的信号相对相位保持不变。这样的重新组合得到的正弦波具有与之前一样的幅度。
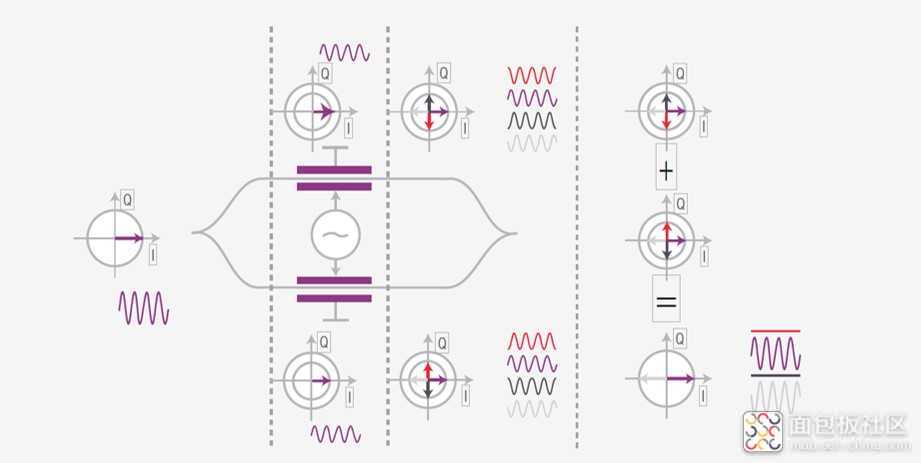
图 29. Mach-Zehnder 调制器的相移、时域及 IQ 图示例
在红色示例中,信号在下分支上经历了π ⁄2 的相移,而在上分支上的经历了 3π ⁄2 的相移。深灰色示例则与之相反。两个示例的共同点是 :两个支路信号合成时,光信号会产生相消干涉,即两个矢量相加为零矢量。因此,红色和深灰色示例中,调制器输出端没有信号。
在浅灰色示例中,Mach-Zehnder 调制器的电压进行了调整,使得信号在两个分支上的相位都偏移 π。如果叠加这两个信号,会产生相长干涉。所生成的正弦波信号的原始振幅偏移 Φ = π。
用于 QPSK 信号传输的 Mach-Zehnder 调制器如何在采用了QPSK 调制的发射机设置中使用 Mach-Zehnder 调制器?图 30 是完整的发射机设置方框图,并简要介绍了QPSK 调制原理。
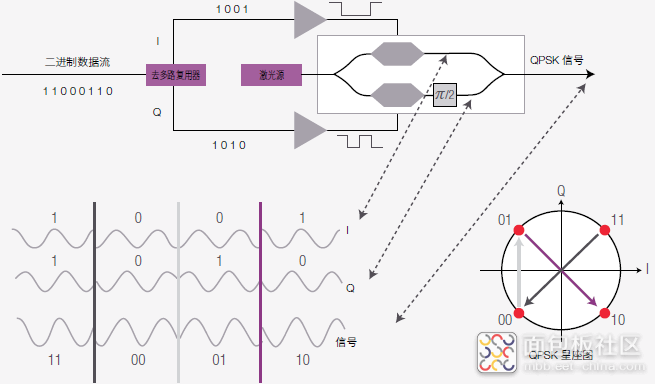
图 30. 用于调制 QPSK 信号的发射机设置
QPSK 调制在 1 个符号中编码 2 个比特,因此传输速率比 OOK 快一倍。4 个符号在 IQ 图中表现为处于同一个圆的 4 个星座点,这意味着我们仅在一个振幅上处理信号。这些点之间的间隔为 π ⁄2。
在发射机中,电比特流由去多路复用器分为信号的 I 和 Q 部分。这两个部分都可以直接 对 Mach-Zehnder 调制器支路激光信号的相位单独进行调制。使用另一台 Mach-Zehnder调制器调制下方支路(Q 支路)信号,实现 π⁄2 的相移。两个支路信号重新组合之后,得到图 30 下方所示的 QPSK 信号。
更复杂调制方案的发射机设置如果需要实施 16-QAM 等更高阶的调制方案,发射机设置必须提供更多的幅度电平和相位,这将进一步增加发射机的复杂程度。16-QAM 调制要求每个符号编入 4 个比特,因此需要两个光功率电平。多种调制方案都可以满足要求,这些方案的不同之处在于其模块化水平以及电域或光域的调制性能。图 31 是四种实施方案的对比。
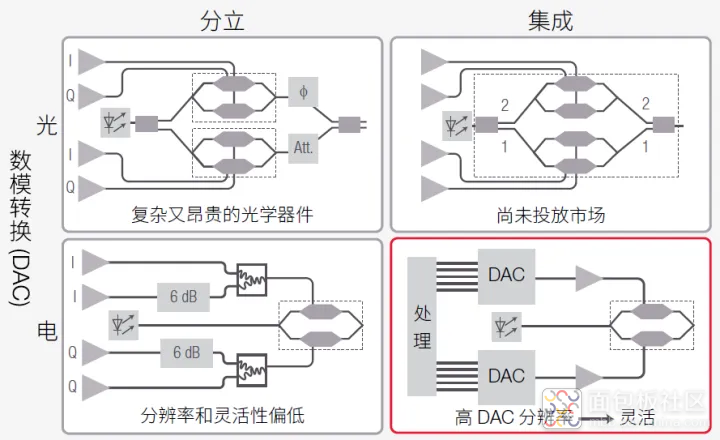
图 31. 用于除 QPSK 以外调制制式(例如 16-QAM)的发射机。在实际应用中,通常使用右下角的电路
左上角是一个由分立元器件构成的发射机。对光信号进行数模转换 (DAC)。以 BERT 为例,四个输出通道用来生成每个符号的 4 个比特,四个电压驱动两个 Mach-Zehnder 调制器。激光源及随后的分路器提供两个光信号,光信号通过 Mach-Zehnder 干涉仪完成调制。 在下方的支路中,光衰减器可以获得第二低的光幅度。相对于下方支路,上方支路中的第二台 Mach-Zehnder 调制器对信号执行相移。两个支路信号重新组合,可以得到 16-QAM光信号(即干扰信号)。这个电路的缺点是必须使用多个价格高昂的 Mach-Zehnder 调制器。此外,铌酸锂器件必须保持相同的恒定工作温度,以确保精准的相位控制。这是一个严峻的挑战。
如何探测复合调制的光信号
我们刚刚说明了复杂光调制方案对发射机体系结构的影响。接收机方面也需要新概念,这并不足为奇。
如果将Mach-Zehnder 干涉仪集成到一个光学芯片上,那么可以更容易控制相位,如图31 右上方的示例所示。这里,分支1 和2 均发射QPSK 信号。两个分支的干扰结果是16-QAM 信号,如图32 所示。这种方法的缺点是这种芯片还没有上市。
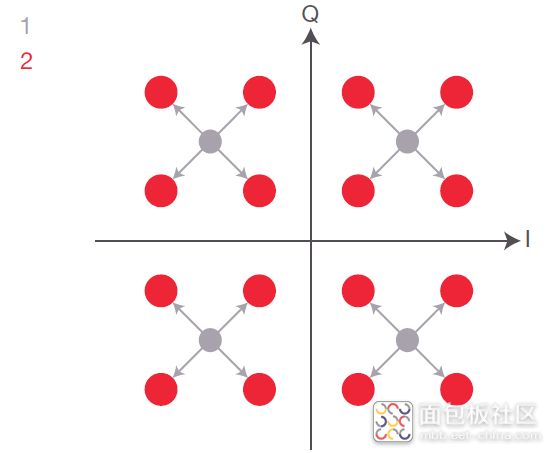
图32.16-QAM 调制的两个并行步骤:对其中一条支路上的浅灰色QPSK 信号进行调制,将其与另一条支路上的QPSK 信号卷积,生成红色的16-QAM 星座点。
图31 左下方显示的是两个在电域进行数模转换的设计。标准码型发生器可用于创建4 位序列。信号I 分量输入上方的两个支路,其中一个支路的衰减器提供第二幅度电平。下方两个支路也具有相同的情况,其中的信号Q 分量保持原始值。经过合路器之后,两个电信号可以控制Mach-Zehnder 调制器中的光信号。该方法的缺点在于:由于包含众多元器件,电路非常复杂,而且缺乏灵活性。由于电压分辨率不足以支持两个以上的幅度电平,因此这种方法无法实现64-QAM 等高阶调制方案。
图31 右下角示例是最便捷灵活的方案。实际上,这是通常使用的发射机实施。信号由任意波形发生器进行调制,然后驱动Mach-Zehnder 干涉仪。使用这种方法可以生成更多的电平。使用这种光发射机可以实现比16-QAM 更复杂的调制方案。
在 OOK 中,可以通过光电二极管轻松检测信号,光电二极管将光功率转换为电流 IPhoto。光电二极管生成的光电流 IPhoto 与光信号 S 及共轭复数 S* 的乘积直接成正比。图 33 的公式显示,运算结果仅包含幅度 AS,IPhoto 不会提供关于角频率 ωs 和相位 Фs 的任何信息。因此,右侧时域图的 QPSK 信号无法明确地与左侧 IQ 图直接映射。唯一能够确定的是,下方通过“零”的曲线表示 4 个星座点的对角转换,而中间的曲线表示外转换。通过“1” 的平坦信号表示相位不变的情况,意味着符号后面紧跟的是同一个符号。
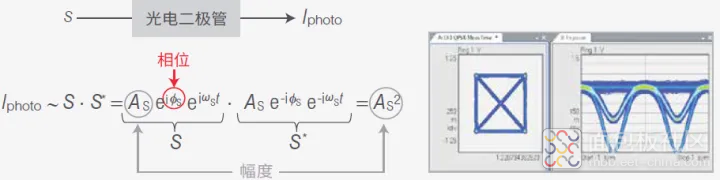
图 33. 应用直接探测方法时,光电流 I Photo 仅提供光幅度信息。
为了明确识别符号转换,我们需要采用更为复杂的方法,以检测包括相位信息在内的完整电场。
如何检测光信号的相位?
当代光纤通信系统的工作波长接近红外光波,典型波长为 1550 nm,对应的频率为接近200 THz,这无疑增加了光信号探测的复杂程度。并且,电场的时间和空间变化速度远高于幅度,现有 MHz 至 GHz 工作频率的电子设备根本无法满足任务要求。
可以使用本地振荡器
解决这两个问题的关键在于不要测量绝对相位而是测量相对于已知参考信号的相位。
图 34 所示为一个基本的信号探测设置,生成参考信号 R 的理想单色激光源通常称为 “本地振荡器”。
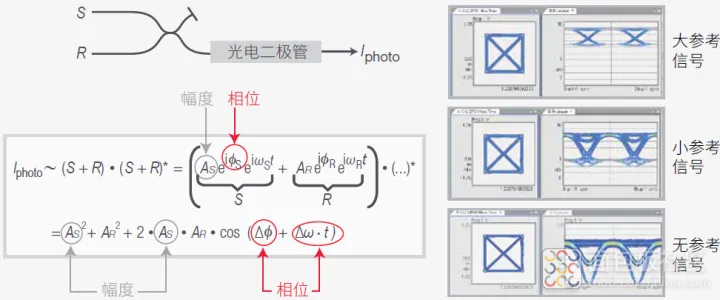
图 34. 将信号 S 与参考信号 R 混合,可以测量相位差。与不同参考信号混合的 QPSK 信号。 注意 :我们只能检测相位差,频率差表现为线性相位随时间发生的变化。
应用光合成器叠加关注的信号 S 和参考信号 R,然后使用光电二极管探测叠加信号。 IPhoto 与两个信号之和 (R+S) 及其复共轭 (R+S)* 的乘积成正比。图 34 中的等式表明,结果的相位差为 ΔФ = ФS – ФR,频率差为 Δω = ωS – ωR。现在,从 ΔФ 可以推导出 ФS 随时间的演变。
选择接近 ωS 的参考频率 ωR,如此一来,Δω 就足够小,可以通过电子方式进行处理。
相位相关项称为外差项或拍频项,是两个信号混合或“拍频”的结果。
公式中还包括一个平方幅度项,该项只对相位进行调制且幅度保持不变,也就是 QPSK调制的情况下,不会产生任何影响。
图 2下方是无参考信号时的结果视图。如前所述,视图仅包含 AS2 项。
如果添加的参考信号大于信号本身,拍频项会向上相移 AR2。仅计算无相移的拍频项较为简单。
使用平衡接收机抑制与相位无关的项
如图 35 所示,可以使用平衡接收机来抑制所有其他与相位无关的项。待测信号 S 和参考 信号 R 在 2x2 光合成器(光纤或自由空间光耦合器)的一条支路叠加,并在另一条支路 相减。使用光电二极管探测生成的信号,并且应用两个光电流的差值。在图 3 给出的公式中,我们可以看到所有其他项都已抵消,只余下拍频项。
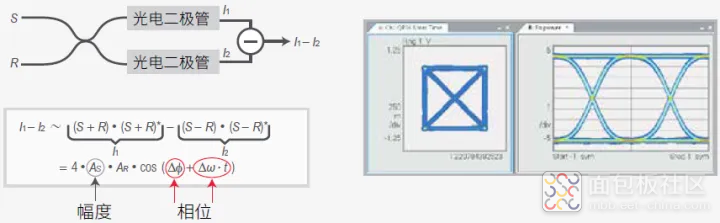
图 35. 使用平衡接收机时,只有拍频项仍然保持双倍强度。注意 :平衡检测使得信号加倍并消除信号的 功率和参考,但我们仍然可以看到相位和幅度的乘积
平衡探测的另一项优势在于:净光电流将翻倍。
将这个概念带入 IQ 平面——IQ 解调器
为了恢复幅度和相位,相干接收机应当将同相 (I) 分量和正交 (Q) 分量作为两个单独的输出信号提供。为此,我们需要第二个平衡探测器。单个本地振荡器可为两者提供参考信号,但相移幅度必须为 π/2,才能获得 Q 分量。图 36 是一个用于 QPSK 信号的探测设置,称为“IQ 解调器”。
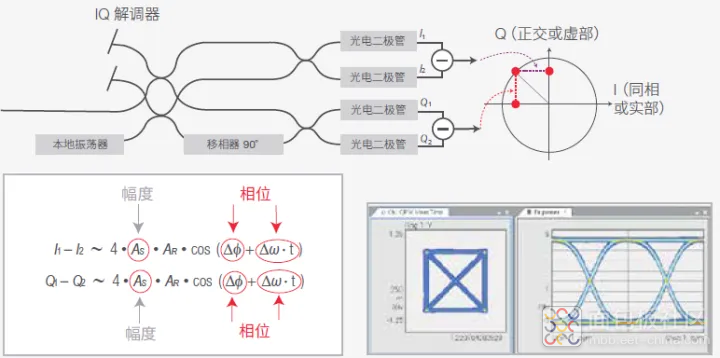
图 36. IQ 解调器可以提供两个同时包括幅度和相位信息的独立测量。注意 :通过添加第二个平衡探测器, 我们可以进行两次独立的测量,其中包括我们现在可以恢复的信号幅度和相位
该设置仅适用于未偏分复用的相干信号。并且,相干信号仅混合具有相同检波器端偏振状态的本地振荡器信号分量。
将这一概念扩展到双偏振
在双偏振方面,解调器概念需要进一步发展。基本原则保持不变:在偏振分束器之后放置两个 IQ 解调器分别用于 x 偏振和 y 偏振。仅使用一个本地振荡器为所有分路提供参考信号。
参见图37 中的方框图。有四个输出信号用来分辨 I 坐标和 Q 坐标,每个偏振方向分别对应一个信号。公式中的上标指数 h 和 v 表示信号相对于接收机偏振参考帧的水平和垂直偏振状态。偏分体系结构能够确保所有信号都与本地振荡器混合,无需考虑偏振输入状态。该结构因此得到了广泛应用,甚至包括未采用双偏振的信号。
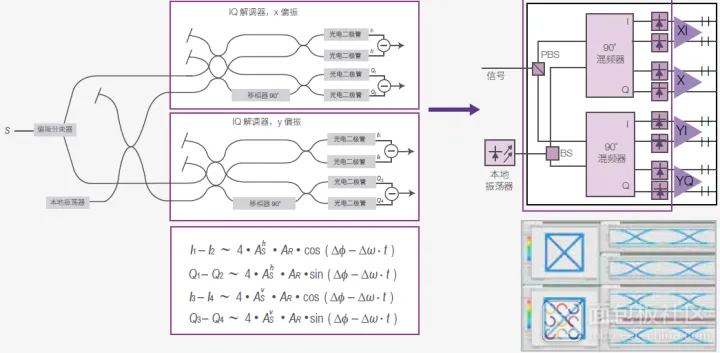
图 37. 用于偏振分辨测量的 IQ 解调器
到目前为止,我们针对本地振荡器频率为 ωR(该频率不同于信号频率 ωS)的接收机进行了研究。此类接收机称为外差接收机。
在零差接收机中,本地振荡器的频率与载波信号相同。优势:上述各项不再与频率相关。
图 38 量化分析了零差接收机和外差接收机需要的电带宽。零差接收机中,本地振荡器与信号的频率相同,因此零差探测所需电带宽是信号光带宽的一半。外差接收机中,本地振荡器与信号间存在频偏,因此需要更宽的电带宽。
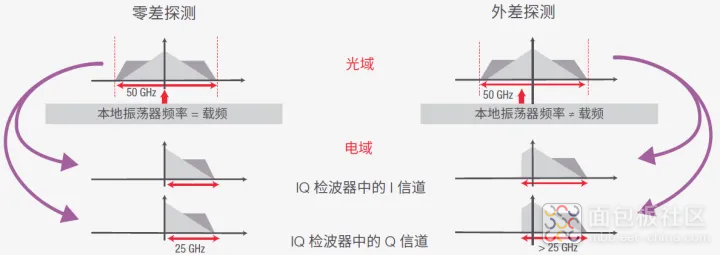
图 38. 相干探测需要的电带宽取决于信号与参考之间的频偏。
使用信号的时延副本作为参考——时延线干涉仪
要恢复相位信息,本地振荡器似乎不可或缺。我们也可以用信号自身的副本来覆盖信号。这样就能得到参考信号,其中 ωR = ωS。
也许有人会质疑该方法的效果,因为这样可能无法提供明确的相位信息。但是,自零差方法非常实用,因为它可以检测相位随时间的变化。因此,如果信号被分成两部分并且使用时延的信号副本作为参考信号来进行覆盖,那么可以获得相位变化信息。
该测量方法的优势在于,外部本地振荡器和载波激光频率波动(相比码率)速度较低导致的精度下降不会对测量产生影响。
此类接收机设置称为时延线干涉仪。图 39 是一个平衡时延线干涉仪,包括信号 S(t) 和时延了 T 的信号 S (t+T)。
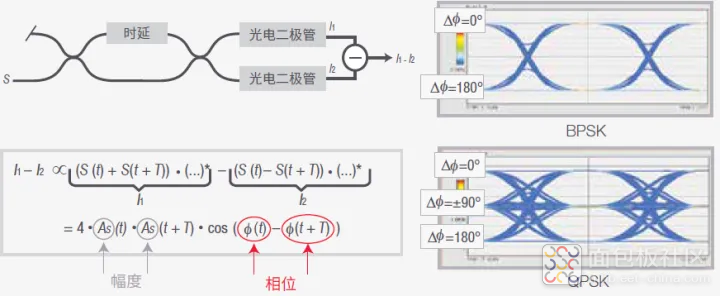
图 39. 平衡时延线干涉仪
这个公式表明,结果取决于原始信号与其时延副本之间相位差的余弦。考虑到函数的周期性,我们只能确定 0 和 π 之间的相位差,以及信号延时 T 约为载波周期 2π/ωS 的整数倍。这些数据足以探测 BPSK 信号,但为了测量 QPSK 及更高阶调制方案的相位恢复时间,必须增加另外一个时延线干涉仪,这个干涉仪相对其他时延线干涉仪相移了π/2,以覆盖从 0 到 2π 的完整相位范围。
图 40 是添加了另一台时延线干涉仪用于接收两个独立 I 和 Q 分量的电路。单独测量 Q1 – Q2,同时 I1 – I2 保持不变。
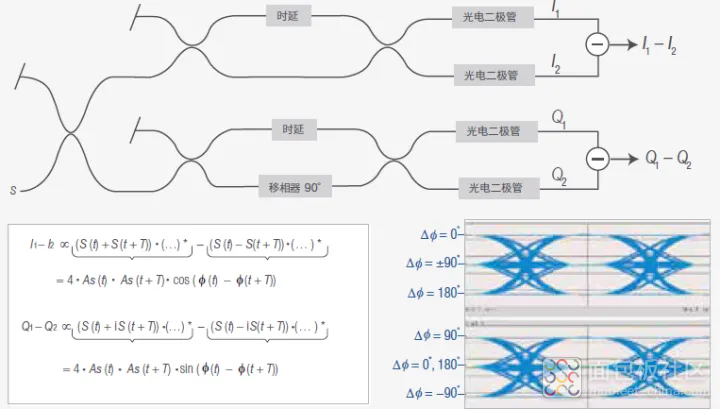
图 40. 用于 QPSK 和更高阶调制制式大的扩展时延线干涉仪
延线干涉仪与外差接收机类似,扩展后可用于偏振敏感型测量。
使用时延线干涉仪的话,则无需使用外部本地振荡器。因此,我们可以避免振荡器带来的相位噪声,所需处理的信号也更少。然而,该方法仍然存在不足,因此我们不得不选择外差接收机。
首先,在没有时钟数据恢复 (CDR) 功能的条件下使用时延线干涉仪测量相位随时间的变化,时延和采样周期需要明显低于符号周期,而当前极高的码率无疑会带来几乎不可能克服的挑战。另外,在测量低功率信号时,低功率参考信号和传输链路噪声累积会降低测量灵敏度。对于应用采样技术的设置,测量时间将延长,并且需要使用触发。最重要的是,零差接收机的灵活性较低。
到现在为止,我们针对时域检测技术专门进行了探讨。此外,可以对频谱进行检测,并通过傅里叶变换推导出时域信号。
频域探测
要通过频谱恢复一个复合调制信号,我们必须执行复合频谱测量,包括幅度和相位测量。
复合频谱分析仪能够通过色散元件分离不同的光频率分量,并完成复合频谱测量。应用多台检波器可以同时探测所有频段,也可以使用扫描窄带光滤波器和单台检波器完成顺序测量。
为了恢复相位和幅度信息,我们再次使用本地振荡器来提供参考信号。为了恢复两个分量,我们使用一台信号源来发射两个光频段的信号。
图 41 是完整的偏振解析复合频谱测量设置。
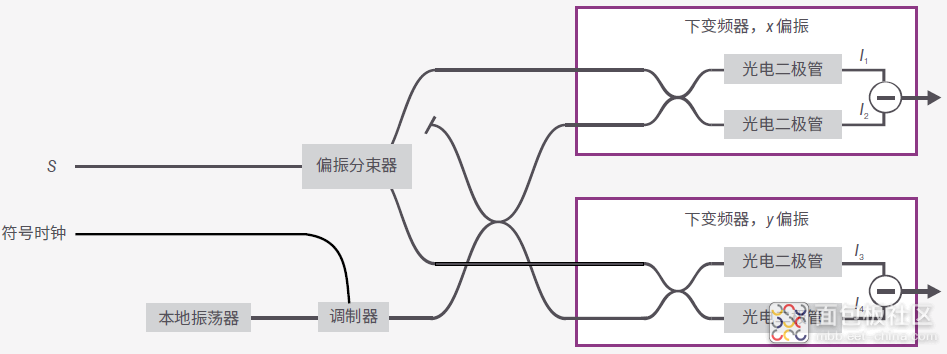
图 41. 偏振解析相干频率探测电路
频域探测的主要优势在于,该方法具有几乎无限的带宽,意味着无限的时间分辨率。 带宽取决于本地振荡器的扫描范围,因此我们可以借助外部可调谐空腔激光源实现 THz的带宽。另一项优势是无需使用高速接收机。
但是,频域检测也存在不足。
该方法仅适用于周期信号,因为周期信号可以生成所需的离散频谱峰值。另外,我们现在需要一个符号或码型时钟。时域信号精度与频谱分辨率直接相关,频谱分辨率决定可恢复的边带数目。受目前最高频谱分辨率的限制,码型长度在几十个符号以内。
综上所述,加上无法提供实时结果的不足,频域方法并不适用于网络接收机。事实上,这意味着测量时间会加长,测量设置和信号处理过程会变得复杂。
最后,频域方法会因平均方法消除所有的非周期效应。偏振模色散 (PMD) 同样如此, 且无法得到补偿。
如何选择?
自零差设置无需大量的信号处理工作,并且受相位噪声的干扰较小。但该方法的灵活性较低,必须采用与设计接近的码率,且灵敏度低于外差接收机。
外差时域探测法具有最高的灵活性。与频域探测不同,外差时域法支持实时测量,可用 于检测数据网络的实时信号。等效时间采样仅适用于长度有限的重复信号。借助实时采样技术,我们能够在所有域中重建完整的信号,并且不会受到调制制式的限制。外差时域检测中的信号长度没有限制。PMD 和 CD 可以在信号处理过程中得到补偿。因此, 信号处理速度是唯一限制吞吐量的因素。
要注意的是,该方法要求使用四通道高速设备,需譬如一台能够在整个频率范围内提供极低抖动和噪声并具有高有效位数 (ENOB) 的高性能实时数字化仪。
相干光接收机的相关问题
我们之前介绍了最灵活的检测电路是使用外差时域检测器,它适用于测试信号和实时信号,并且不受调制制式的影响。
图 42 中左侧的器件就是这种 IQ 检波器。此图清晰地说明,在识别并进一步分析符号中编码的输入比特之前,还有几个步骤需要完成。此处所示的接收机体系结构是光互联论坛 (OIF) 的推荐设计,它能够提取信号中的所有信息。详细检查接收机体系结构。
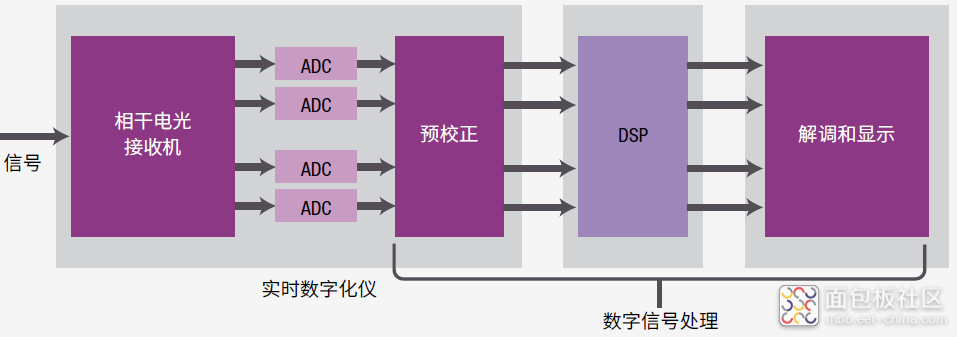
图 42. OIF 建议采用的集成内差相干接收机体系结构 ( 《用于集成双偏振相干接收机的 OIF 实施协议》,IA # OIF-DPC-RX-01.2,2013 年 11 月 14 日 )
大幅降低减损
光信号在经过模数转换后,还需要进行 DSP,这个步骤对于任何相干光接收机都是不可或缺的。传统的开/关键控存在 CD 和 PMD 信号失真效应,与之相比,使用 DSP 可以获得明显的优势。DSP 支持通过算法补偿 CD、PMD 和其他减损,因为相干检测可以提供完整的光场信息。这意味着采用复合光调制,我们再也不必使用 PMD 补偿器或色散补偿光纤,也不会因为这些模块增加的损耗和时延而头疼。
上游预校正步骤可以消除接收机缺陷。这些缺陷可能包括四个电通道之间的通道不平衡、 IQ 混频器的 IQ 相角误差、四个 ADC 通道之间的计时偏移,以及正常平衡接收机的差分不平衡。要消除这些减损,通常需要在进行仪器校准时,在波长范围内执行器件表征。
除了接收机带来的这些缺陷之外,DSP 还必须补偿信号经过发射机和接收机之间的光路径所发生的衰减,其中包括 CD 和 PMD、偏振相关损耗 (PDL)、偏振旋转或偏振态转换(PST) 和相位噪声。
为了评估相位噪声的影响,可以跟踪载波相位随时间的变化。不过,这个步骤在相干接收机设置中不是必需的。
载波相位恢复
通过引入本振,我们可以跟踪信号相位在不同时间相对本振相位的变化。但实际上外差接收机场景中的本振与信号之间存在频率差,导致相位漂移会随时间发生线性变化。只要记住在外差接收机中,IPhoto 与 cos(Δφ + Δω t) 成正比(如何检测复合调制的光信号),这一点就很好理解。图 43 所示为 QPSK 调制的这种“旋转”星座图。
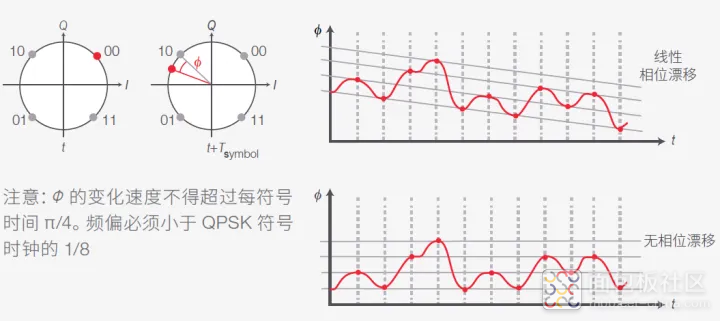
图 43. 发射机激光源与本地振荡器之间的频率差会使星座图发生“旋转”。
为防止模糊,相位的变化速度不得快于每符号时间 π/4,即两个相邻符号之间的相位差的一半。这意味着本振和信号之间的频偏必须小于 QPSK 符号时钟的 1/8。
为了能够跟踪相位,信号采样必须在相位值可预测的时间点(例如在符号时间处)执行。对于有限带宽的信号,相位采样率小于符号率。图 44 中深灰色线显示相位可能没有正确恢复。
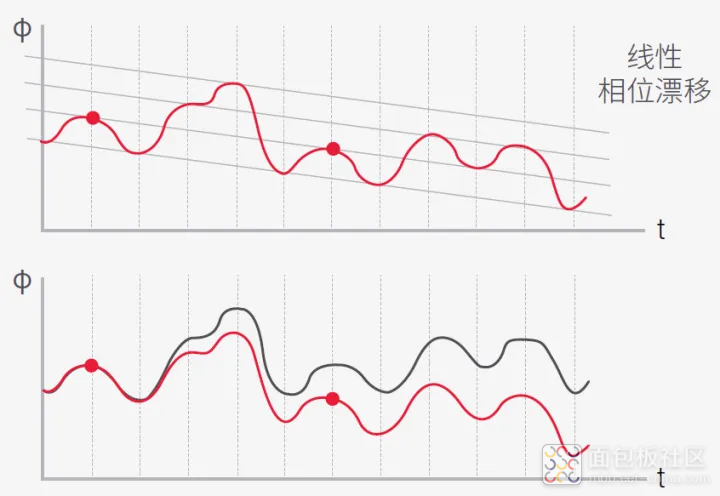
图 44. 在实际传输系统中,由于采样率太低,再考虑到相位噪声和偏移,相位通常不可能恢复。
在这些情况下,载波相位噪声和偏移必须遵循非常严格的限制,以使相位可以恢复。在实际传输系统中,通常不会出现这种情况,因为在执行实时采集的实际线路卡中不需要遵循这些更严格的规范。
图 45 显示了载波带宽对 DFB 激光源相位恢复的影响。左侧是高跟踪带宽实例。IQ 图中的星座点人为缩窄,因为在这种情况下相位跟踪会减少符号的角宽。较低的带宽带来的是更逼真的圆形符号。随着带宽进一步变小,在载波相位图中我们已经达到极限,不可能再跟踪相位。无法消除的相位噪声会对符号角展度产生明显影响。
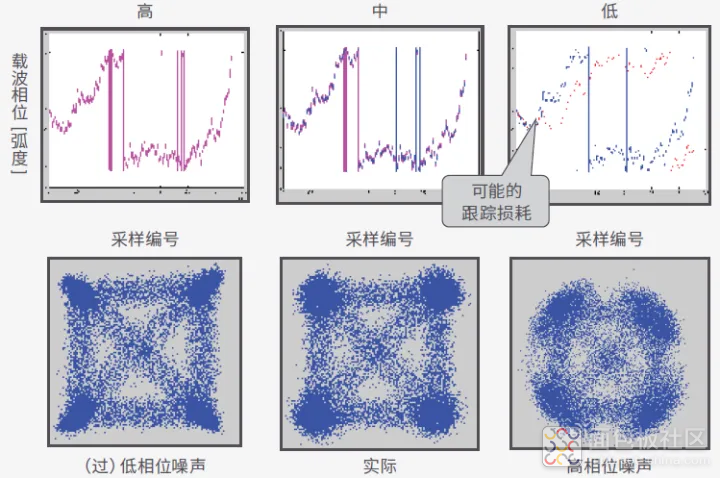
图 45. 这个示例表明,DFB 激光源的载波相位跟踪取决于跟踪带宽
找到 Jones 矩阵以恢复原始偏振态
为了给数字解调器提供两个独立的基带信号(用于 x 偏振和 y 偏振),需要在 DSP 中进行偏振去多路复用这一步骤。在这个步骤中,必须对 PMD 和 PDL 进行补偿。还需要考虑的是,在单模光纤 (SMF) 中,传播期间不会保持偏振态。
沿着信号通过光纤的路径,偏振方向会逐渐发生变化(图 46),因此终端的偏振态 (SOP)不仅仅与接收机的方向有关。如果接收机中存在偏振分束器的话,我们无法获得两个独立的信号,而只能得到这两个偏振信号的线性组合。偏振维持光纤可以保留 SOP,但是由于它们的衰减更大,价格也更高,因此不会在数据传输中部署。
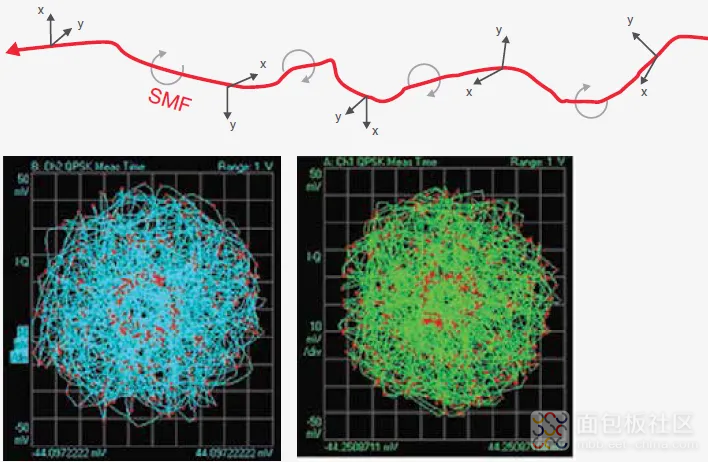
图 46. 单模光纤改变了发射光的偏振态。因此,接收机一侧的偏振分束器不提供 2 个独立信号, 而是提供线性组合,这里是偏振解复用之前的双偏振 QPSK 星座图示例。
光纤通道中全偏振光的所有衰减效应,均可用 Jones 矩阵进行数学描述。发送信号 S乘以 Jones 矩阵,即得到接收信号 R。对于没有减损的理想信道,Jones 矩阵是一个恒等矩阵;接收信号与最初发射的信号相同(参见图 47)。Jones 矩阵最常见的形式是一个复杂的 2x2 矩阵,其中含有 8 个独立的实时参数。

图 47. 理想信道的 Jones 矩阵
必须确定 Jones 矩阵以便从测得的接收信号中推导出原始信号。由于我们对信号在信道中的减损效应大小了解极少,因此很难完成以上任务。
为此,我们通常采用所谓的“盲算法”来近似估算原始信号。这些估算方法不要求我们了解原始信号(调制制式除外)。这里,我们用串联的均衡滤波器(图48)来过滤接收信号,得到 Jones 矩阵的倒数。每个滤波器元件建立一种信号衰减效应的模型。该算法迭代搜索滤波器变量组 (α、β、k...),最终得到收敛结果,这意味着测得的符号以最小误差映射到该算法计算得出的符号。
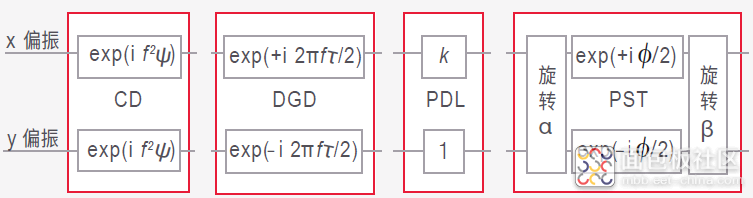
图 48. 用于补偿色散 (CD)、差分群时延 (DGD)、偏振相关损耗 (PDL) 和偏振态转换 (PST) 的 均衡滤波器模型 . ( 1. J. C. Geyer,F. N. Hauske,C. R. S. Fludger,T. Duthel,C. Schulien,M. Kuschnerov,K. Piyawanno, D. van den Borne,E.-D. Schmidt,B. Spinnler,H. de Waardt,B. Lankl 和 B. Schmauss :《偏振多样性相干接收机的信道参数估算》,IEEE 光子技术快报,第 20 期,第 10 号,2008 年 5 月 15 日)
这种方法的缺点是同一个偏振信道可能会恢复两次。这个问题被称为该算法的奇异性。这种方法也非常复杂,因为每个符号都必须单独处理,才能计算下一个迭代步骤。
在 Stokes 空间中更容易估算
使用 Stokes 空间可以更容易估算。在 Stokes 空间中,由于无需进行解调,也无需知道使用的调制制式或载波频率,所以偏振去多路复用是真正的盲程序。此外,Stokes 空间中没有奇点问题。
Stokes 空间可帮助显示光信号的偏振条件,因此是观察光信道中偏振变化的出色工具。完全偏振光的任何偏振态都可以通过球体表面上的三维空间点来描绘,所谓的 Poincaré球的中心位于这个坐标系的原点。球半径对应光幅度。沿着 S3 轴可以找到圆偏振。S1和 S2 轴所跨越平面的赤道上是线性偏振,中间位置表示椭圆偏振。图49 中,我们可以看到球体上有一些绿色的独立偏振态。
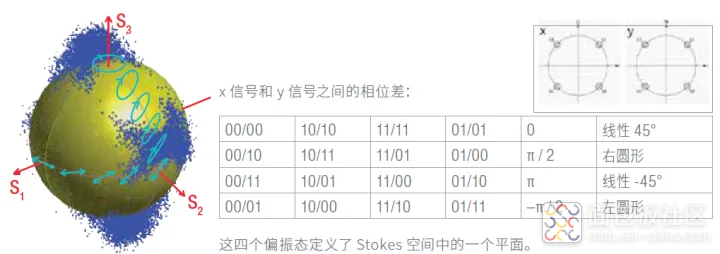
图 49. 偏振多路复用 (PDM) QPSK 信号的 Stokes 空间中的 Poincaré 球
图 49 中还显示了测得的 x 偏振和 y 偏振 QPSK 信号。这两个信号在采样点上有四个可能的相位差。通过 x 信号和 y 信号与这四个相位差的组合,可以得到 Stokes 空间中测得的蓝点云。(使用只有一个偏振方向的 QPSK 信号,我们只能在 S1 轴上获得一次累积。)
四个偏振态之间的转换在 Stokes 空间中定义了一个类似透镜的目标(参见图 50)。由此可见,任何制式的偏振多路复用信号都可以定义此类透镜。
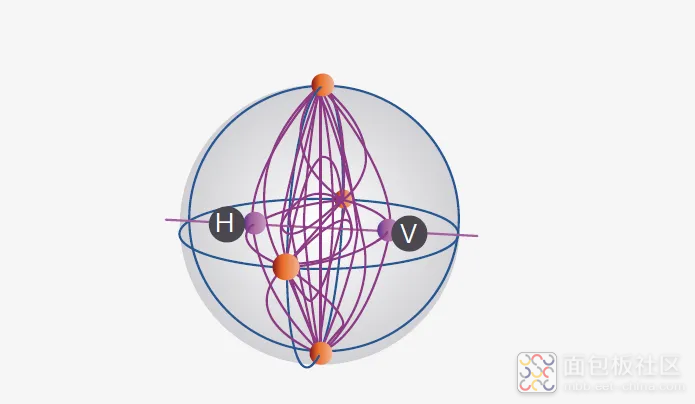
图 50. PDM QPSK 信号的符号之间的跳变,在左半球中,x 偏振信号(H :水平)的跳变和右半球的 y 偏振信号(V :垂直)
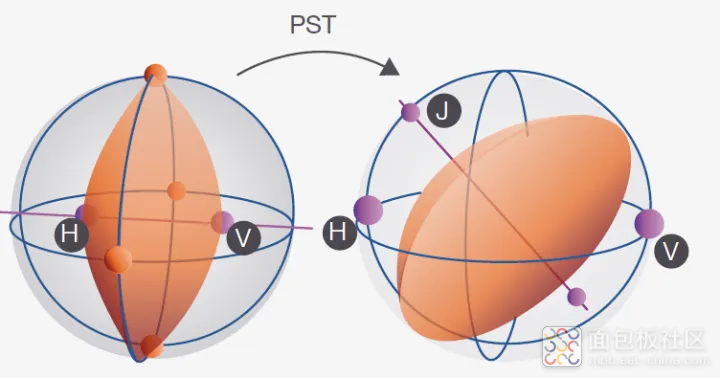
图 51. PST 导致透镜在 Stokes 空间旋转。透镜的法向定义了 Jones 矩阵――此处以 PDM QPSK 信号作为实例。
当我们面对沿着单模光纤光路径的 PST 时,透镜在 Stokes 空间中旋转(参见图 51)。根据 旋转,我们可以推导出 Jones 矩阵,即类似透镜目标的法向。
如何在 Stokes 空间中表现其他信号衰减效应?PDL 会使透镜发生变形和位移。但这并不影响 Jones 矩阵的恢复。通过变形,可以定量确定 PDL 的大小。CD 与偏振无关,也不 会妨碍偏振去多路复用。在这种情况下,星座图是进行定量研究的最佳工具。
符号的确定
成功完成 DSP 之后,接收的符号得以最终确定。在 QPSK 中,判定标准是星座图中测量点的 I 和 Q 值(参见图 52),例如每个具有正 I 和 Q 值的点都理解为“11”。在更先进的制式中,不可能简单地将 I 和 Q 值当成判定标准。这些点被指定给最近的符号。通过 图 10 右侧的扩散云,我们可以看到即使使用相干检测,还是会出现比特误码。如何量化确定这些问题?
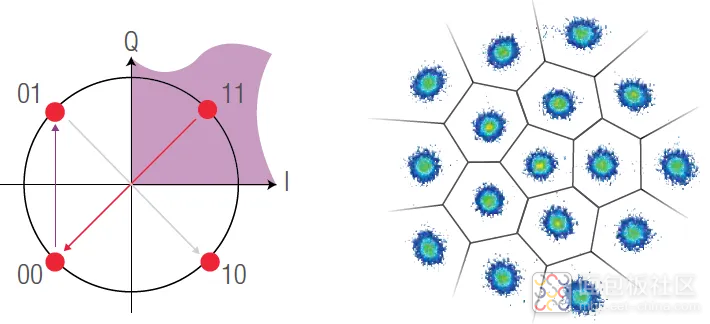
图 52. 在 QPSK 中,根据 I 值和 Q 值,在距离最近邻居的距离上采用更高级的制式
相干测量的质量评定
复合光调制方案需要在发射机和接收机侧采用新方法。前面文章表明,相干传输并不比传统的 OOK 更复杂。数字信号处理 (DSP) 是相干接收器的组成部分,可以减轻色散带来的减损影响。这是相干概念带来的额外好处。
然而,相干系统同样会产生其他失真,因此全面的误差分析必不可少。现在的问题在于,这里是否也需要新的概念?
传统质量参数
我们来看看 OOK 已知的质量指标。这里有比特误码率 (BER) 和 Q 因子,它们可以从假设高斯噪声分布的眼图来进行估算。
以 100-Gbps 传输系统常用的复合调制制式—QPSK 调制为例,我们可以绘制眼图来推导上述质量参数。尽管相位是 QPSK 中唯一的变量参数,有一种更为实用的方法是使用两个独立的眼图,将 I 分量和 Q 分量分别映射到两个独立眼图中。
图 53 的 I 眼图中,0 到 1 跳变用紫色表示 ;在 Q 眼图中,1 到 0 跳变用红色表示。由于 I 和 Q 分量已解耦,我们无法明确对应上述信息与 IQ 图的符号转换。左侧实例可能是01 或 00 到 11 或 10 的跳变,存在 4 种可能的跳变。Q 跳变映射存在同样的可能。
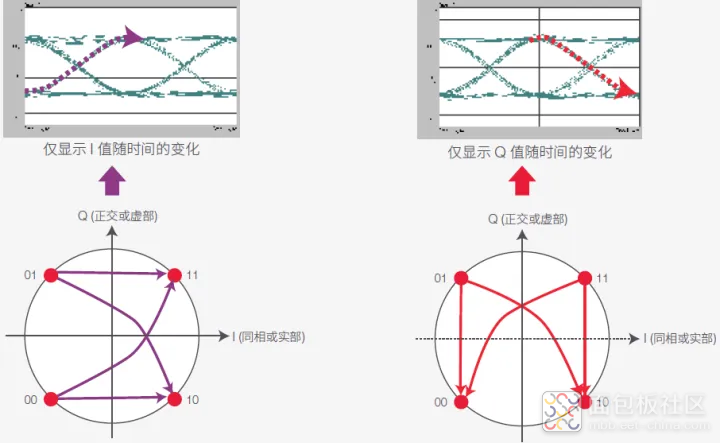
图 53. QPSK 信号中 I 分量和 Q 分量的眼图(单偏振)。IQ 图的符号跳变映射始终不清晰。 I 和 Q 路径的时序偏差只能通过 IQ 图显示
缺乏明确的映射并不一定会导致问题。但是,IQ 图中包含独立眼图无法显示的失真。 图 1 中,量个 IQ 图中的弯曲斜线跳变(参见图 53)显示调制器 I 和 Q 路径之间存在计时偏移。I 明显早于 Q,但在两个独立眼图中看不到这一点。
如果采用更先进的制式,事情将变得更加复杂。图54 所示为一种特殊的 16-QAM 制式。如何将其映射到眼图?
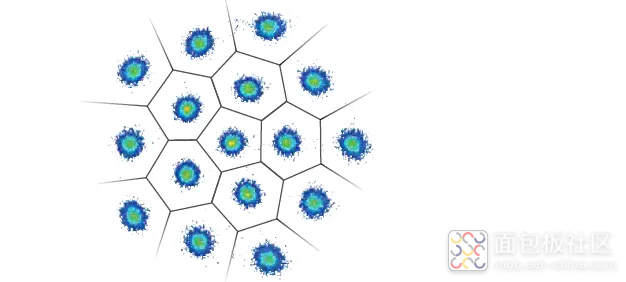
图 54. 特殊 16-QAM 制式的测量星座图
这个图也告诉我们,复合调制会在 IQ 平面上决定接收比特的序列。因此在同一幅图中判断质量更为便利。在这个视图中,有一些失真更为明显。
误差矢量幅度(Error Vector Magnitude) (EVM)
我们再次通过射频社区了解到,早在几年之前工程师就采用直观的方法从最近的理想星座点获取测量点距离,妥善解决了这个问题。这个概念不会产生歧义,并且适用于可以在星座图中表示的各种调制制式。
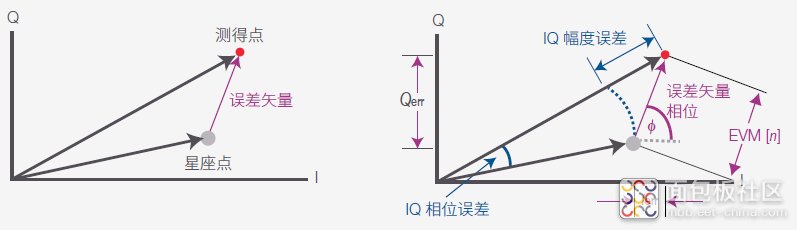
图 55. 误差矢量和误差矢量幅度的定义
“推荐阅读,了解三种准确进行和优化EVM测量的最佳实践”
图 55 所示为是某个测得点的误差矢量幅度。误差矢量幅度 EVM[n] 是测得点与理想参考点之间的欧几里德距离:
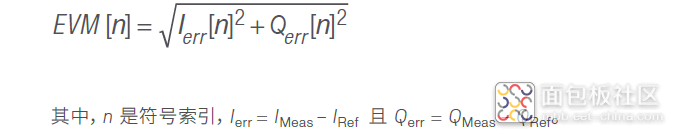
标准均平方根平均误差矢量幅度定义为:


除以峰值参考矢量的幅度可以实现归一化。其他定义使用所有参考矢量的平均幅度或平均功率,在比较 EVM 值时可能导致混淆。
图 56 所示 QPSK 信号实例中,四个星座图点周围的测得红点具有 5% 的误差矢量幅度。
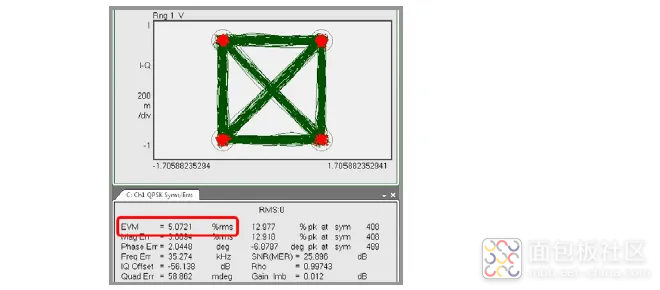
图 56. 在 QPSK 信号上测得的 EVM
信噪比 (SNR)
从 EVM 中还可以导出信噪比 (SNR)。它也称为调制误差率 (MER),其定义是发射信号的平均符号功率与噪声功率之比。这包括导致符号偏离理想状态的各种项 :

BER 估算
如果只存在高斯噪声,则可以直接从 EVM(归一化到所有参考矢量的平均幅度)来预测 BER。
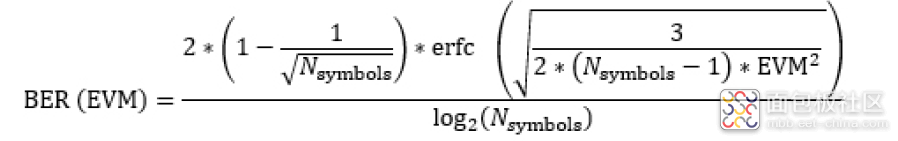
N symbols 是星座图中符号的数量,erfc 表示互补误差函数,log2 是以 2 为底的对数。如果EVM 同时包括其他失真,预测将更为复杂。测得的 BER 并未升至使用简单模型时的预期水平,因此预期 BER 提供的是上限。在信号不包括任何噪声但星座图失真时,上述情形尤其明显。此时,EVM 会有一个值,预测 BER 也非零,但实际的比特误码值可能为零。
借助误差矢量幅度 EVM(Error Vector Magnitude)获得深入见解
目前为止,我们只了解了符号时间的误差矢量幅度。观测 IQ 图中的跳变并绘制随时间或频率变化的 EVM 图,可以帮助我们找到失真的根源。
图 57 中有两个例子。左侧的例子将测量信号与“无限”带宽的参考信号进行比较;右侧的例子将相同的测量值与使用升余弦滤波器创建的参考信号进行比较。两个实例在符号时间上的 EVM 值相同。
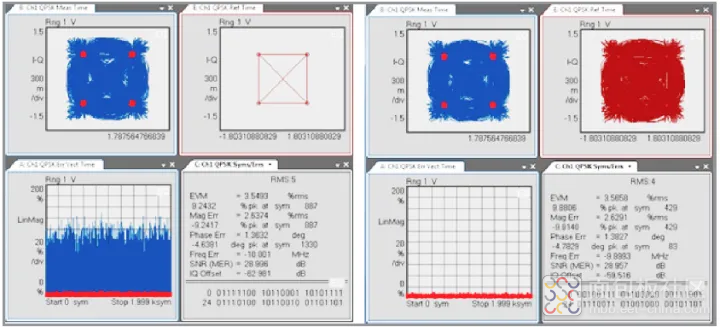
图 57. 决定时间上的 EVM 相同,但 EVM 时间趋势图显示“无限”带宽有问题(左侧),而升余弦滤波器没有问题(右侧)。
但是,查看 EVM 时间趋势图(下方右侧各个窗口)可以发现,测得信号偏离“无限”带宽参考信号,表现为高 EVM 值。如果发射机使用的升余弦滤波器与参考信号使用的滤波器具有相同特征,我们可以看到符号跳变时 EVM 值较低(右侧)。这一分析有助于在从一个符号到下一个符号的跳变阶段发现发射机信号中的无用特性,除了 EVM 之外,IQ 图还可以推导出其他误差参数,帮助我们找到光学系统中各种问题的根本原因。
增益失衡

增益失衡比较的是 I 信号的幅度和 Q 信号的幅度,以 dB 表示。
图 58 所示为一个大约 2dB 的增益失衡,表明存在问题。I 和 Q 的幅度相差 1.26 倍。
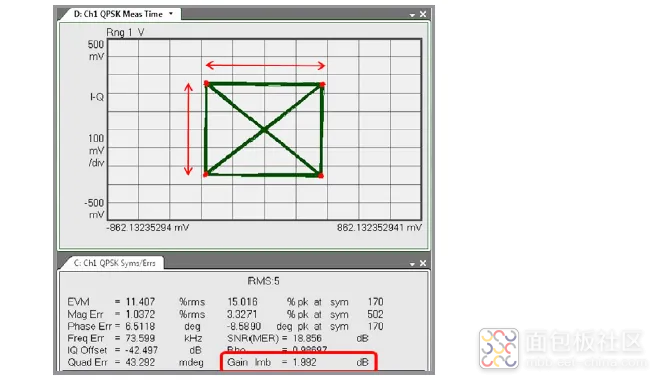
图 58. 增益失衡 :IQ 平面中的 I 幅度大于 Q 幅度。
增益失衡可能源于发射机端 Mach-Zehnder 调制器的射频驱动幅度失衡。
IQ 偏移
IQ 偏移(也称为 IQ 原点偏移)表示相对于原点的星座图(图 59)偏移(中心频率功率与平均信号功率的比值)。
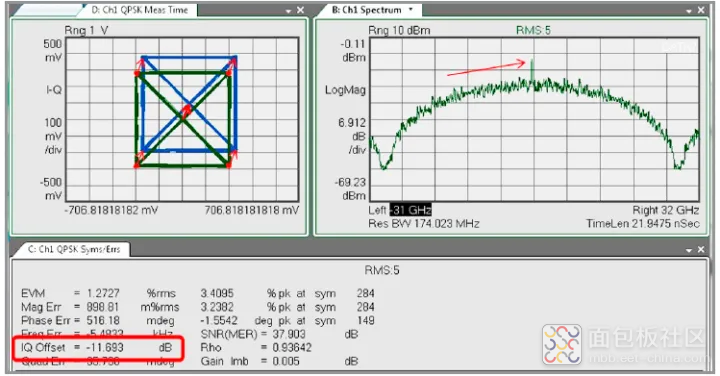
图 59 .IQ 偏移:IQ 图已偏离原点
这一结果指示的是载波馈通信号的幅度。当不存在载波馈通时,IQ 偏移为零(-无限 dB),表示为信号与偏移比 :
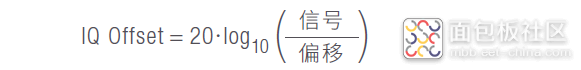
IQ 偏移通常是由调制器 I 或 Q 路径中的直流偏置或是由微小的射频驱动幅度和错误偏移点导致的。
正交误差
正交误差量化确定了 I 和 Q 之间正交性的像差。在理想的情况下,I 和 Q 应该为正交(相隔 90 度)。
图 60 所示的例子中,可以看到约 10 度的正交误差,意味着 I 和 Q 相交角度为 80 度。
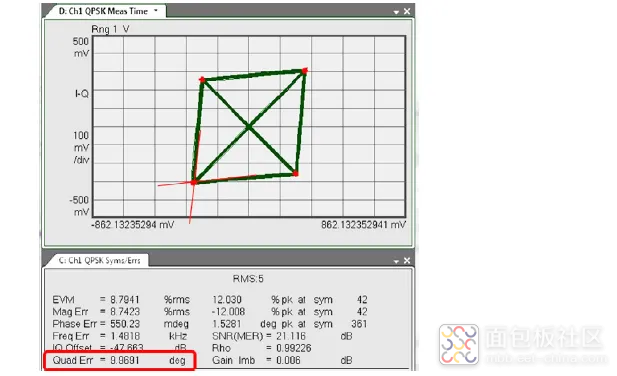
图 60. 正交误差 :I 和 Q 相位非正交。
正交误差通常表示发射机存在问题,IQ 90 度移相器可能存在错误偏移点。本例中同样包括眼图失真。
通过调整 Mach-Zehnder 干涉仪的偏置电压可以实现 I 和 Q 路径正交。
频率误差
频率误差表示载波频率和本地振荡器频率之间的频率差。这个误差数据的单位为 Hz,表示 为了实现载波锁定必须在数字域中添加的频偏量。可以补偿的最大频率误差取决于使用的调制制式(对比图 61)。

图 61. 不同调制制式的频率误差和最大频率误差示例。注意 :频率误差不会影响误差矢量幅度测量。
IQ 幅度误差
IQ 幅度误差表示测得信号与理想参考信号之间的幅度差异(对比图 55 和图 62):
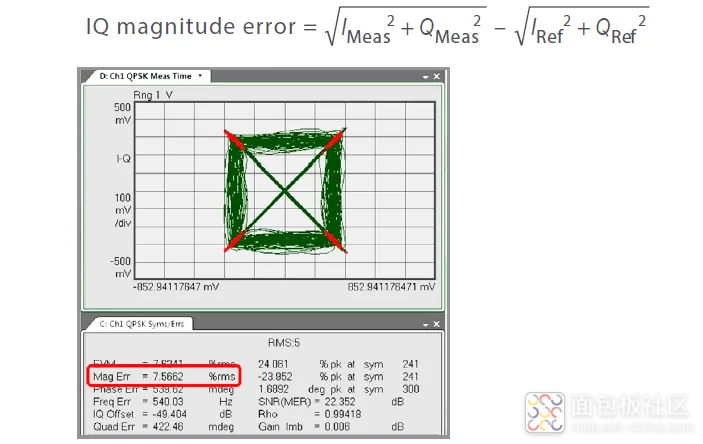
图 62. 误差幅度示例
例如,发射机激光源的低频率强度噪声可能导致幅度误差。
IQ 相位误差和激光源线宽
相位误差是理想 IQ 参考信号与在符号时间测得的 IQ 测量信号之间的相位差(见图 55 和图 63):
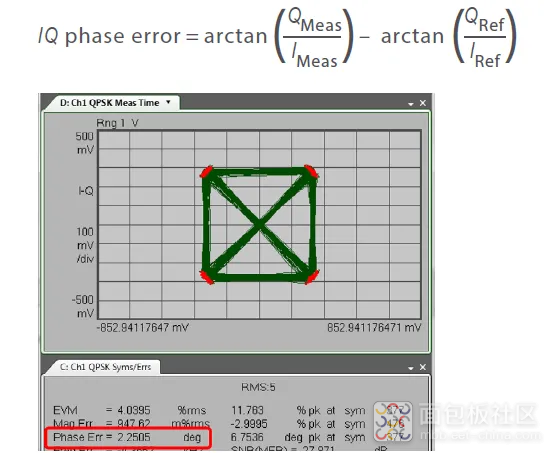
图 63. 相位误差示例
相位误差可能是由载波或本地振荡器激光源产生的相位噪声引起。它还可能导致时变频率误差。激光源的相位误差通常使用激光源线宽来量化。以下程序可以用来估算激光源线宽。使用 Kalman 滤波器相位跟踪算法(参见《基于 Kalman 滤波器的复杂信号估算和解调》),可以评估不同时间及经过傅里叶变换的相位误差,获得相位误差谱。将模型与相位误差谱拟合,可以将激光源线宽估算为自由拟合参数之一。
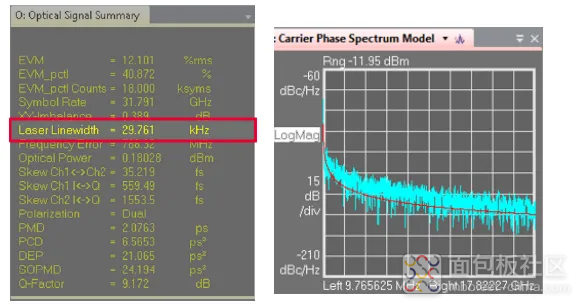
图 64. 激光线宽估算(左)及其与载波相位谱的拟合(右)
什么是IQ 偏差?
IQ 偏差测量发射机每个偏振的 I 信号和 Q 信号之间的时序偏差。这可以通过使用以下公式来测量符号时钟的相位差完成 :
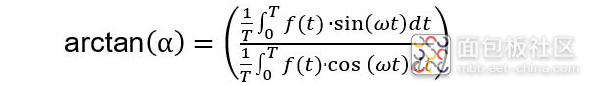
IQ 偏差会导致 IQ 曲线失真并使得 EVM 增加。在查看相应的 I 和 Q 眼图的叠加时,可以看出它们相对于彼此有位移。如果星座图非常干净,那么还可以观察到,向上和向下的45°跳变会采用不同的路径。
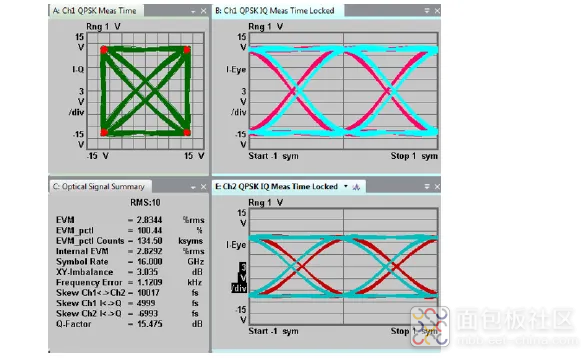
图 65. IQ 偏差示例
X-Y 偏振偏斜和失衡
x 偏振和 y 偏振之间也可能存在时序偏差。它的计算公式与 IQ 偏差相同。x-y 偏振偏差不是用于信号质量测量的关键参数,但是,在各个比特流失去同步之前,实际网络接收机可能只能容忍一定量的 x-y 偏差。请注意,是德科技 OMA 软件只会报告 x-y 偏差的数值。由于应用了时序校正,相应眼图不会显示偏差。
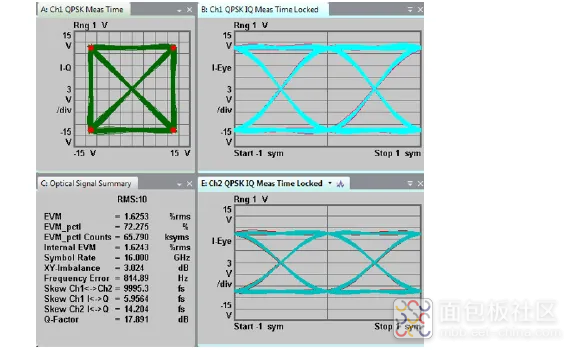
图 66. 失衡偏差示例
x-y 偏振失衡是由 x 偏振和 y 偏振功率电平的差异造成的。光功率电平 Px 和 Py 的最大功率变化 ΔPpol 使用以下公式计算 :
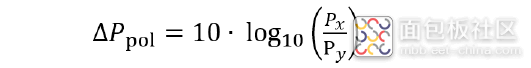
相干数据传输的未来
复合光学调制不仅仅是在数学意义上具有复杂性。但是,它的频谱效率比其他直接传输制式都高,因此尤其适用于较长距离和较高数据速率的传输。然而,即使是在诸如城域网和数据中心互连 (DCI) 这样的短距离中,相干调制也取代了一部分传统的直接检测传输制式。一般来说,数据速率越高,在短距离上使用直接检测技术也就越困难,而另一方面,在针对短距离进行优化时,相干传输技术可以简化。这意味着,随着数据速率提高,相干检测越来越有可能成为首选的技术。未来将会告诉我们,相干检测将会通过哪些应用在价格、尺寸和功耗方面赶上直接检测。
来源:是德科技






 /4
/4 

