运放这个器件相对于电阻,电容,三极管,MOS管等器件算是比较复杂的,而且电路中也常用,出问题的情况也多,显然一篇文章根本就说不明白运放,因此,可能要写很多期。
首先,第一个问题,为什么要说理想运放呢?
因为一般来说,我们了解一个东西,都是先将它当做理想来看的,这样最为简单,也最容易懂。
当我们拿到一个陌生的电路,首先我们肯定是要知道这个电路是干什么用的对不?
这个时候我们就先不用考虑电路中器件的非理想特性,比如先不考虑温漂,漏电,寄生电感,寄生电容等等这些。我们就先把它当做理想的,然后看这个电路到底实现了什么功能,运放电路一般也是这么分析的。
等我们知道这个电路是干啥用的,然后再看看器件的哪些特性会导致这个电路失效,或者说不按照预期的工作,这个时候就要考虑非理想特性了。
所以,我们了解理想运放的目的,就是为了在一开始的时候能快速的分析出电路的工作原理,实现了什么功能。
理想运放主要有以下三点:
- 1、增益无穷大
- 2、输入阻抗无穷大
- 3、输出阻抗为0
那么这三点特性又是怎么来的呢?
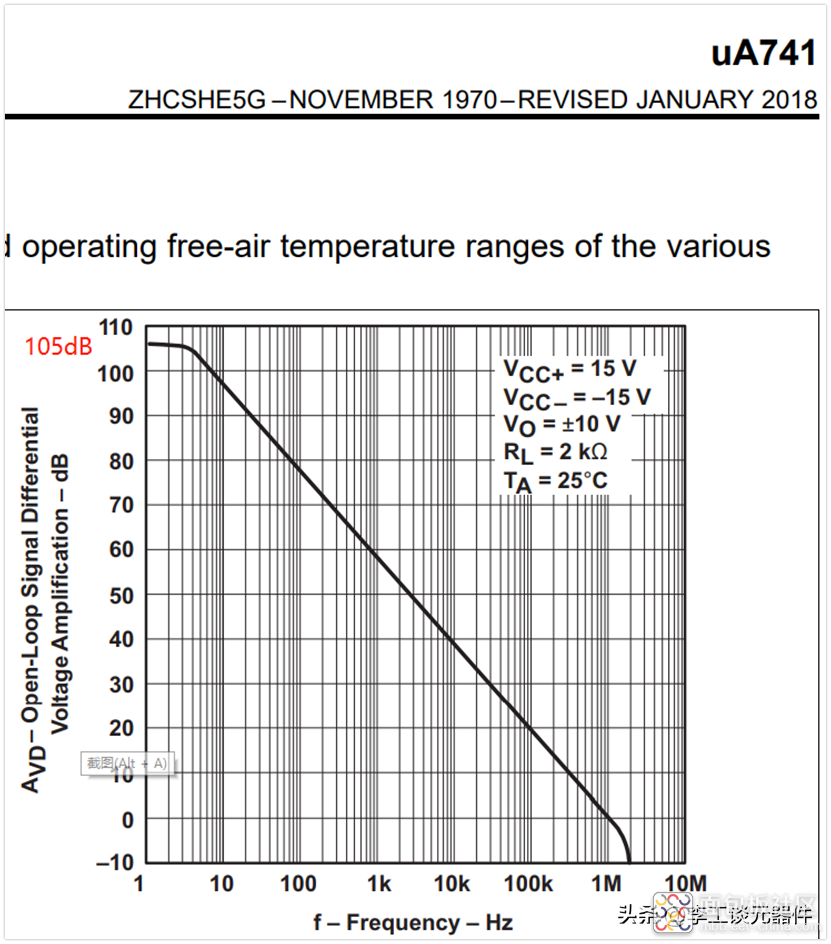
增益无穷大好理解,因为一般运放的增益就是很大的,比如Ti的uA741,开环增益是105dB左右,计算一下是多少倍呢?
20log(Av)=105dB,计算得Av=10^5.25=177828,大约是18万倍。相对于我们一般电路中几十倍的放大倍数,这个很大了。
理想运放的输入阻抗无穷大,我们看看实际运放的,还是以Ti的uA741为例,如下图:
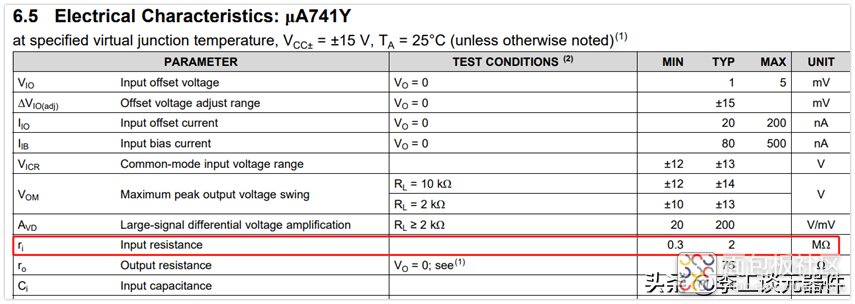
可以看到,输入阻抗还是比较大的,典型值是2MΩ,其实这个芯片在运放中阻抗算是偏小的了。比如TI的另外一款芯片LM358的输入阻抗就更大,差分输入阻抗10MΩ,共模输入阻抗4GΩ。

总之,运放的输入阻抗就是比较大的,因此呢,我们在进行原理性,分析电路工作原理的时候,就是把运放的输入阻抗看成是无穷大的。
理想运放的输出阻抗可以看成是0。
一般我们不会用运放直接驱动大功率的负载,而运放的输出阻抗一般也就是几十Ω或者上百Ω,相对后级来说,输出阻抗可以忽略,因此可以将运放的输出阻抗看出无穷小,也就是0,这样分析起来方便,而且结果也不会有太大的差异。
比如ti 的uA741的输出阻抗为75Ω
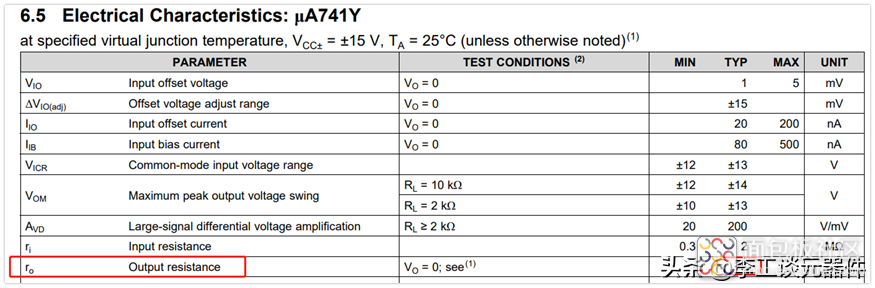
ti的LM358输出阻抗为300Ω。

可能有人会认为,这阻抗也不是很低啊,咋就能忽略呢?
这个其实还是看应用,如果运放后端的电路等效输入阻抗比较高,那么自然就可以忽略的。如果负载的输入阻抗本身也就只有几十或百Ω,那么自然就不能完全忽略。
以上就是理想运放的三个最大的特点,我们在拿到一个电路后,利用这三个特点,一般就能将运放电路的基本功能给分析出来。
但是可能会问这个问题:我们通常明明是利用运放的“虚短”和“虚断”分析电路的,根本就不是上面说的的这三个特点,那这又是咋回事呢?
答案其实也很简单,那就是运放的“虚短”和“虚断”,是根据上面理想运放三个特点推导出来的。
“虚断”相对于“虚短”来说,相对简单点。
前面说理想运放的输入阻抗无穷大,解读一下就是说,如果给运放的输入端加个电压,那么流入流出运放的输入管脚的电流就是0,阻抗无穷大嘛,自然没有电流,那就相当于是开路,也就是断路。但是呢,这跟完全断路又不一样,因为运放还是会感应输入端的电压的,所以也不是真的断路,因此,称为“虚断”。
可以看到,“虚断”跟把运放接成什么样的电路没有关系,只要是个集成运放,都可以运用虚断来分析(严格来说,实际运放输入端还是有电流的,只是相当小。如果外部电阻实在太大,导致电阻电流接近或者超过运放的输入端微小电流,“虚断”还是会失效的)。
相对于“虚断”的基本无门槛使用,运放的“虚短”使用是有门槛的。
先说结论,虚短使用有两个条件
- a、电路为负反馈电路
- b、运放工作在线性放大区
要理解这两点,我们只需要知道“虚短”是咋来的就好了。
首先,虚短的意思是什么呢?
我们知道,运放有两个输入端,同相端和反相端,“虚短”说的就是同相端和反相端的电压一样,就跟短路一样,那它是如何做到这一点的呢?我们前面说的理想运放的三个特点也没有这个呀?
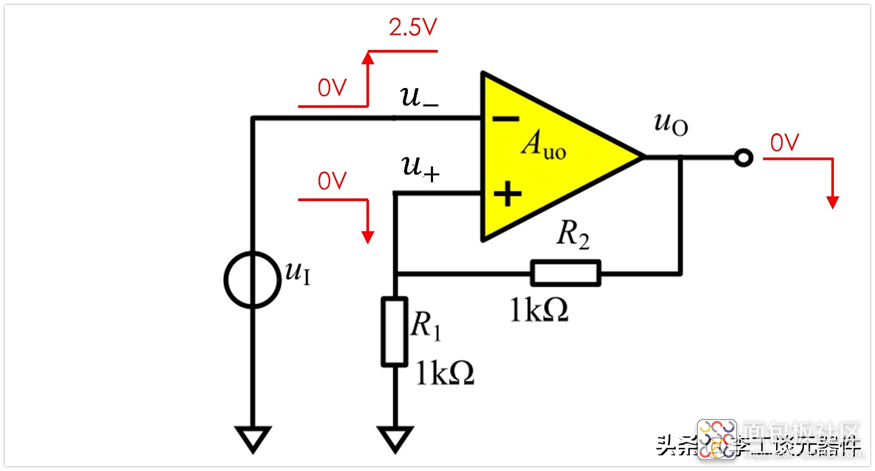
下面就以下图的电路为例子,看看为什么最终是u+ = u-的?
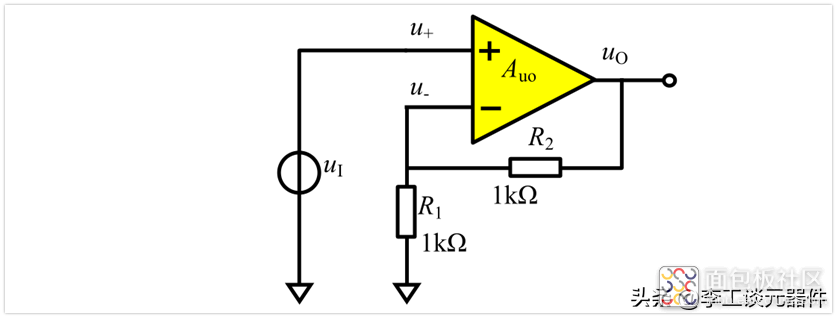
假设刚开始时,各处电压为0,突然u1瞬间从0变为2.5V,因为uo一开始为0V,根据“虚断”,u-没有电流流入放大器,所以u-为uo在R1和R2上的分压,依然为0V。
当u+瞬间为2.5V后,u-为0V,u+>u-,放大器会朝着电压增大的方向进行放大,即uo电压会开始升高。
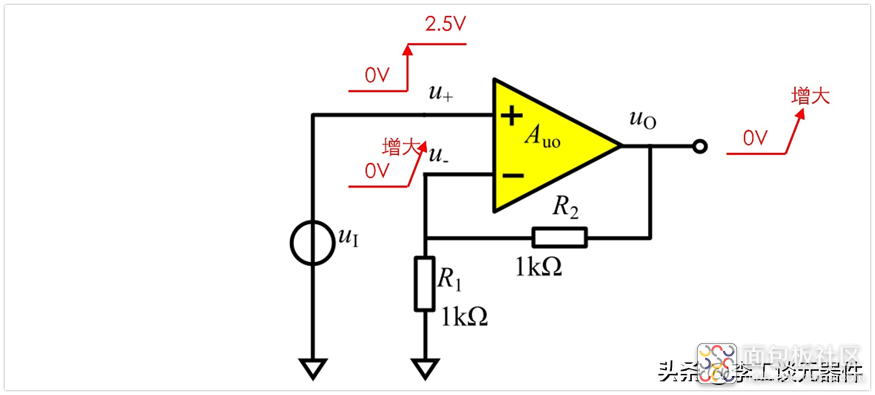
当uo增大到1V,u-依然为uo的在R1和R2上的分压,即为0.5V。此时u+=2.5V,u-=0.5V,u+>u-,放大器将电压继续正向放大,因此uo继续增大。
那问题来了,uo增大到多少会停止呢?很容易想到,只要u+>u-,因为我们现在讨论的是理想运放,放大倍数为无穷大,所以uo就会增大(放大器是这样一个装置,它总是将输入电压放大Auo倍,即总满足:Uo=Au*(u+ - u-))。
只有当uo增加到5V时,u-电压为uo在R1和R2的分压正好是2.5V,u-等于u+,此时放大器达到平衡,不再放大,即稳定态就是现在了。
那为什么稳定态一定是u- = u+,u- > u+不行吗?
我们也可以假设下,万一uo一不小心超过了5V,那么u-就会大于2.5V,u-会大于u+,此时放大器会将输出电压反方向放大,也就是减小,最终电压还是会向5V逼近。
因此,不论电路初始状态电压是怎么样的,最终输出都会稳定在5V,而且u+ = u-,因为一旦u+不等于u-,那么在无穷大的放大倍数下,输出必然会变化,最终还是会导致u+ = u-。
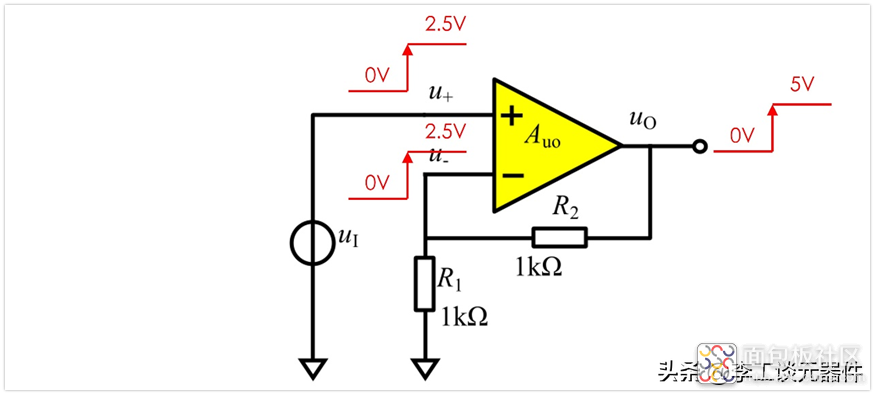
前面这些有点绕,我们仔细想一下,逻辑是不是这样:当u+不等于u-时,输出就会变化,这个变化又会送回到输入端,图中为u-,进而导致u+与u-的差值变小,差值变小,意味着输入信号变小了(运放的输入是u+ - u-,也就是差值)。
也就是说,输出信号将自己通过电阻R2和R1又送到输入端,降低了输入信号,这不就是负反馈吗?
总之,对于上面这个负反馈电路,最终的结果就是:u+ = u- 。
如果我们将运放的同相端和反相端颠倒会发生什么呢?
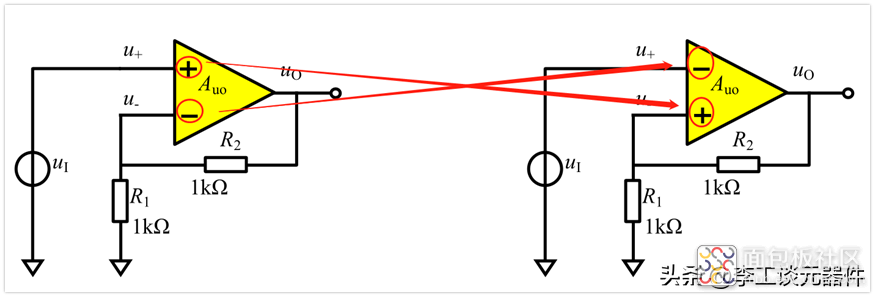
同样的,当输入突变成2.5V,因为uo初始还是0V,那么u+也是0V,此时有u+ < u-,因此,输出要减小,变成负的。当输出减小时,根据分压关系,u+也要减小,也是负的,也就说u+比u-小得更多了,即u+与u-的差值更大了。差值更大,意味着输入信号变大了(运放的输入是u+ - u-,也就是差值)。
也就是说,输出信号将自己通过电阻R2和R1又送到输入端,加强了输入信号,这不就是正反馈吗?
很容易想到,最终的稳态就是uo能输出多低就是多低,如果是单电源供电,那么uo=0V,此时u+=0V,而u-=2.5V,显然,u+不等于u-,也就是说不满足“虚短”
由上面可知,“虚短”必须是负反馈,但是还需要个条件。就是放大器需要工作在线性放大区,为什么这么说呢?
以前面的负反馈为例子,当输入2.5V时,输出就是5V了,但是假如供电只有3.3V呢?
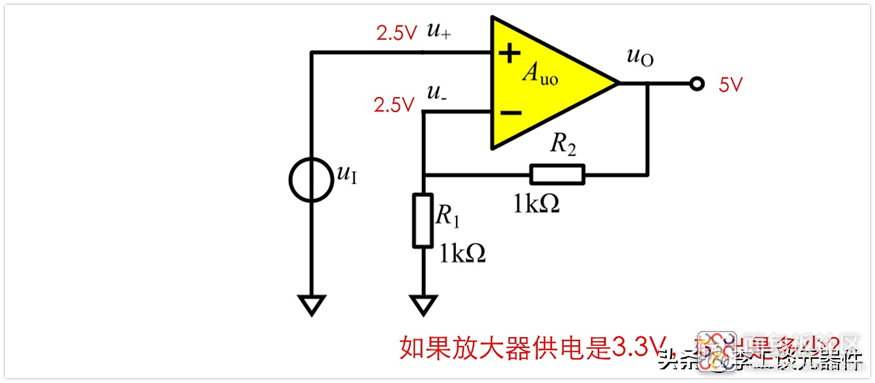
显然,输出超不过5V,此时放大器工作在饱和区,顶天了放大器也只能放大到3.3V,因此输出最终达不到5V,那么u-自然也到不了2.5V了,此时u+也就不等于u-了,也就不满足虚短了。
所以说,满足虚短还需要放大器工作在线性放大区。
这里我们可以再深入下,前面我们把运放当作理想运放,也就是增益无穷大,最终得到u+ = u-,也就是虚短。如果增益不是无穷大,而是一个有限的值,那么u+和u-的关系是怎么样的呢?
首先,我们先思考下,运放到底是个什么东西?
其实运放可以看成一个这样的东西,它总能将u+和u-的差值放大Auo倍。想想,是不是这么个玩意儿,其实它自己也不知道外面到底接了什么电路,反正就将u+与u-的差值,放大Auo倍,然后送到输出uo。
因此,天然就有了这么个公式:
uo=(u+ - u-)*Auo
变换一下,得:
u+ - u- =uo/Auo
uo是一个有限的值,如果3.3V供电,uo不会超过3.3,就假定uo=3.3V吧,假如Auo是一百万倍,Auo=1000000,那么:
u+ - u- = 3.3V/1000000 = 3.3uV
可以看到,u+与u-的电压差值只有3.3uV,这是相当小的,我们在分析电路电压的时候,自然可以忽略这个压差,把它们看成是相等的了,也就是“虚短”。同时,我们也可以看到,运放的开环增益Auo越大,那么u+和u-的越接近,更能看成是“虚短”。
以上就是本节的全部内容了,大致梳理了下理想运放的特点,以及虚断和虚短的意思,来源,以及使用的条件。
- 增益无穷大
- 输入阻抗无穷大
- 输出阻抗为0
- 基本无门槛(来源于运放的输入阻抗非常大)
- 负反馈
- 工作在线性放大区
原文链接:
https://mp.weixin.qq.com/s/mX6JNZOGL8ZE55IQXOq0zw
来源于:公众号(硬件工程师炼成之路)







 /3
/3 
