按照时域采样定理,采样频率≥2倍的信号频率,才能得到信号全部信息。
而以智能车中的编码器测速为例。我们知道测速周期在可接受范围内越小越利于控速,比如2ms。但2ms采样一次速度,究竟能不能得到速度信号的全部信息我们却不得而知,归根结底是因为不知道速度信号的频率是多少。
那么智能车速度信号的频率要如何得知呢?

速度光电编码盘
(回复)提问中的问题包括有三个子问题:
(1)根据采样定理,如何采集速度信号?
(2)使用光电码盘测量速度信号主要误差来源是什么?
(3)根据车模速度控制需要究竟需要按照什么周期采集速度信号?
同学们学习信号采样定理,最容易犯的错误就是机械的照搬定理的结论,却没有注意到定理的使用条件。
信号采样定理的应用条件有两个:一是信号是一个频带受限信号,即信号有一个最高频率;二是除了知道信号频谱的最高频率之外,不再知道其它信号的额外信息了。在此条件下,信号的奈奎斯特频率,即信号的采样频率就是信号的最高频率的两倍。
如果额外还知道信号的其它条件,比如信号是一个窄带信号,除了最高频率之外,还有最低频率;此时就可以使用低得多频率完成信号的采样。这一点可以参照郑君里教授《信号与系统》第三章的最后一个习题。
举一个极端的例子,如果已知信号是一个正弦波,即信号的频谱是一个线谱,此时实际上只需要任意对信号采样三个不同时间的数据,在一般意义上便可以恢复该信号,此时成为信号的参数估计。
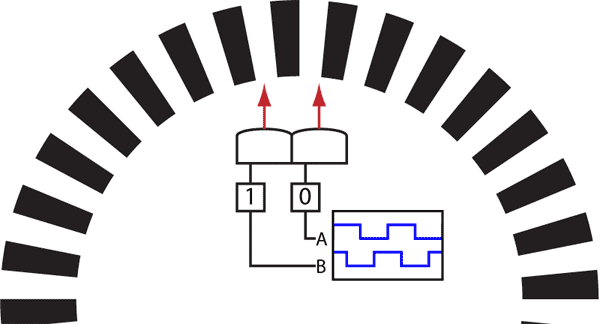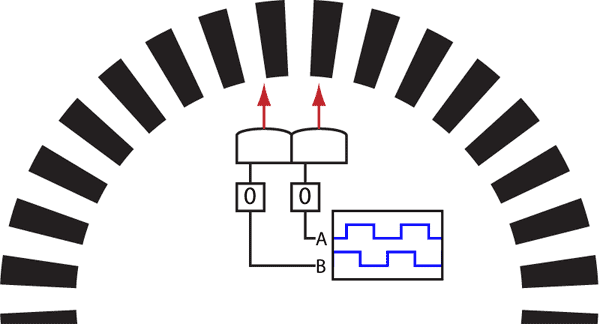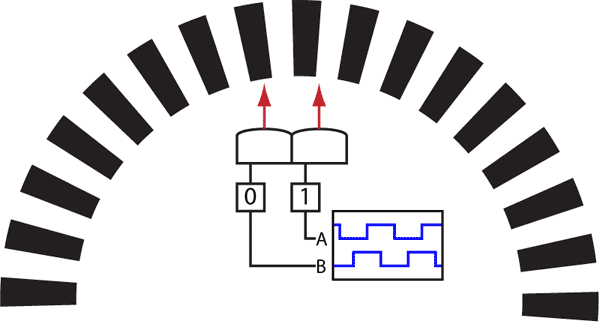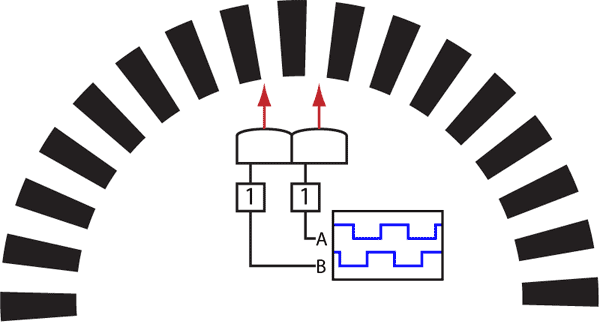
对于车模的速度信号,经过光电编码盘之后,它反映在两路输出正交方波信号中,速度信号是该方波信号的频率参数。
此时可以看成速度信号调制在两路正交同频率的方波脉冲信号中,是调频调制。因此,接受到的光电编码信号是速度信号的调制信号。

接收到的光电编码盘信号是速度的调制信号
所以光电编码信号的频谱并不是速度信号的频谱,而是速度的频谱被调制后进行了频谱搬移。如果对速度信号进行采样,则需要对原来信号进行解调之后才能够获得速度信号。
如何从光电脉冲信号解调出速度信号在第二个小问题进行回答。在此之前,还是需要讨论普通车模的速度信号的频谱范围如何确定?
信号的频谱范围取决于信号的交流分量的范围。如果车模的速度是保持在恒速运行,不论这个速度多大,对应的频谱范围都是0。
那么如何估计车模速度的交变分量呢?这一点可以使用车模从速度为零加速到最高速度的时间,或者从最高速度减速到0 的时间来衡量。这个时间的倒数与速度的频带宽度成正比。
比如车模使用0.2秒从静止加速到最高速度并保持匀速运行,对于这样一个斜边速度信号,它的频谱本身是无穷大的,但可以认为其主要频谱能量集中在5Hz(0.2秒的倒数)以内。对于速度信号的采样可以使用5Hz的两倍以上的频率完成采样,即10Hz以上的采样频率。当然,为了留出一定的余量,则需要使用20H以上的频率进行采样。
具体采样周期需要根据第二个问题-速度测量误差来源和第三个问题车模速度离散控制周期综合确定。
第二个问题是速度测量误差来源。由于常见到的速度编码器是将速度信号调制在两路正交脉冲信号上。

一款实际应用的Hall传感器测量速度
通常可以采用脉冲数量测量方法、脉冲周期测量方法、以及它们的组合方法。测量的误差与总测量时间T成反比,即测量周期越长,所获得的频率越准确。

对于信号的频率估计所产生的不确定性与信号的持续时间T呈现反比关系。这就是著名的信息测不准原理。相关的讨论可以参见推文《傅里叶变换与不确定性》中的叙述。
因此,如果想获得更加精确的速度信息,则需要更长的测量周期,则对应的测量速度的频率就需要越低。最后在结合控制速度的精确度来粗略估计对速度的测量大体精度。
最后一个问题就是关于车模速度控制周期。车模的速度调节是由单片机通过软件来实现的,这是一个离散时间控制系统。其中一个重要的参数,就是离散时间系统的控制周期的选择。
离散时间控制系统的周期在选择上只要比起控制对象的频带宽度对应的时间常数小一个数量级,便可以达到很好的控制效果了。
当确定下速度控制周期之后,对于速度采集的周期(频率)也就相继确定下来了,即速度控制周期就等于速度采样周期。
需要根据控制效果来确定被控对象的控制周期。对于控制效果,往往需要根据控制结果的性能来衡量,它们包括控制量的过冲比率、上升时间、稳定时间以及稳态精度等等。这可以从控制对象的单位阶跃响应曲线来定义。

下面是选择了一个带有0.2秒延迟的二阶系统,它的单位冲击响应如下图所示:

为了提高该系统的性能,即减少系统过冲,同时提高系统的跟踪速度,可以对该系统引入负反馈控制。
下面是引入比例负反馈控制的效果。比例控制参数从0增加到5.

下图给出了在不同的反馈比例因子,反馈系统的过程比率。可以看到,在反馈比例系数为1.75左右时,系统过冲最小,大约在50%的过冲左右。

如果希望进一步减少系统的过冲,可以再引入微分控制项。下图给出了反馈比例系数为1.75,微分反馈控制系数从0增加到1的过程中,系统的单位冲击响应曲线。系统的过冲从50%降低到20%左右。

下图绘制出在不同的微分系数下,系统的过冲变化曲线。在微分系数为0.75左右,系统过冲达到最小。

根据前面两次实验,可以大体确定下系统反馈控制的最优参数,比例系数为1.75,微分系数为0.75左右。
所形成的反馈控制如下图所示:

使用MATLAB的bode命令绘制出此时系统的频率特性:

从上图可以看出,该系统是一个低通系统。但由于延迟的存在,系统具有多个谐振峰值。第一个截止频率在1.6Hz左右,第一个谐振频率在15Hz左右。
对于该系统如果采用单片机软件控制,则需要确定控制周期。控制周期与控制效果之间有什么关系呢?
下图通过实验,对原来的连续控制系统进行离散化,取控制周期0.01s变化到0.75秒,观察系统的单位冲激响应的变化。

下图给出了在不同的控制周期下,系统的单位冲击响应的过冲比率。从图中可以看出,系统过冲量与控制周期之间并不是一个简单的曲线关系,而是随着控制周期增加呈现多次波动情况。
对于一个特定的对象,并不是控制周期越小越好,总是存在着一些最优的控制周期。
对于该系统,当
控制周期超过0.618
秒的时候,反馈系统就不再稳定
,呈现发散状态。

从上面的实验可以看出,对于控制周期小于0.1秒的时候,系统是稳定的,而且过冲误差控制在1.35之内。下面对于控制周期在0.01至0.1秒之间再进行实验,观察在不同控制周期下的控制效果。

下面曲线绘制出在控制周期从0.01秒到0.1秒变化时,系统的单位冲击响应的过冲误差曲线。该曲线呈现规律的波动。
因此,从整体上来看,对于该系统,控制周期只要小于0.1秒,系统过冲就不是很大了。控制周期从10毫秒至40毫秒之间控制性能差别不大了。

最后对于提问的回复进行小结:对于速度信号的测量,它的测量频率不是按照光电编码信号的最高频率来确定的,而是按照其中速度信号的频率来确定采样信号的。速度的频率范围可以从车模加速时间或者停止时间的倒数来近似确定。
最终的速度采样周期则需要跟控制软件周期保持一致。而该周期的确定则是根据控制性能(过冲量、过渡时间、稳定精度等)来权衡。
实践中,在控制性能能够满足要求的情况下,不要一味减小控制周期。这不仅对提高控制性能无益,同时由于对速度采样的周期减少,而带来额外的测量误差。这测量噪声在控制回路中会引起更大的控制噪声。

来源:公众号TsinghuaJoking







 /2
/2 
