在信号处理中,过采样(英语:Oversampling)是指以远远高于信号带宽两倍或其最高频率对其进行采样的过程。一般来说是指采样频率高于信号最高频率的两倍。
高斯白噪声
octave中的awgn函数可以为输入信号in 添加一定大小的噪声。
out = awgn(in,snr,'measured'); 是一种常见的使用方法,意思是在添加噪声前先测量一下输入信号的功率,再根据snr值添加噪声。
信噪比的计量单位是dB,其计算方法是10lg(n/s)。
在下图的代码中,通过y0=round(ay*cos(2*pi*f*t))产生频率为18kHz,幅度为1000,相位随机的输入信号。
out = awgn(in,snr,'measured'); 是一种常见的使用方法,意思是在添加噪声前先测量一下输入信号的功率,再根据snr值添加噪声。
信噪比的计量单位是dB,其计算方法是10lg(n/s)。
在下图的代码中,通过y0=round(ay*cos(2*pi*f*t))产生频率为18kHz,幅度为1000,相位随机的输入信号。
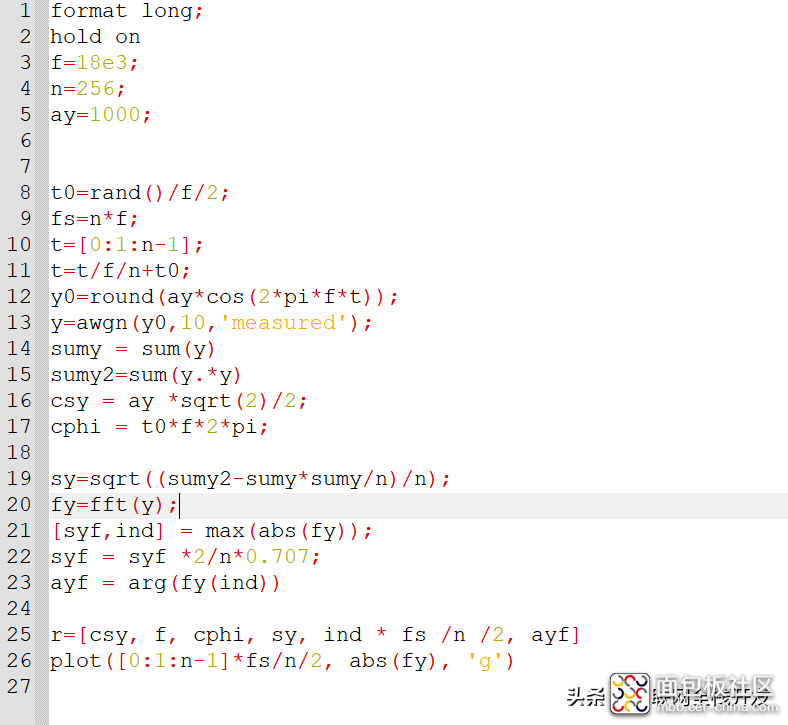
测试代码
第13行代码通过awgn函数往输入信号叠加白噪声,函数返回的新的信号的信噪比由第二个参数指定,该代码设定为10。即为10dB。
假设第i次采样为ADi,则平均功率为:
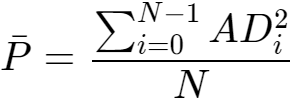
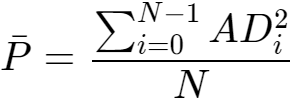
为了深入理解awgn函数,对得到的数据进行验证,
信号一个周期的平均功率:sum(y0.*y0)/n=561646.69。
噪声一个周期折平均功率:sum((y-y0).*y(-y0))/n=49183.81。
信噪比为:10*log10(561646.69/49183.81)=10.57dB,即为函数是第二个参数10dB。
对得到的新信号进行傅里叶变换,并绘制信号频谱曲线,如下:
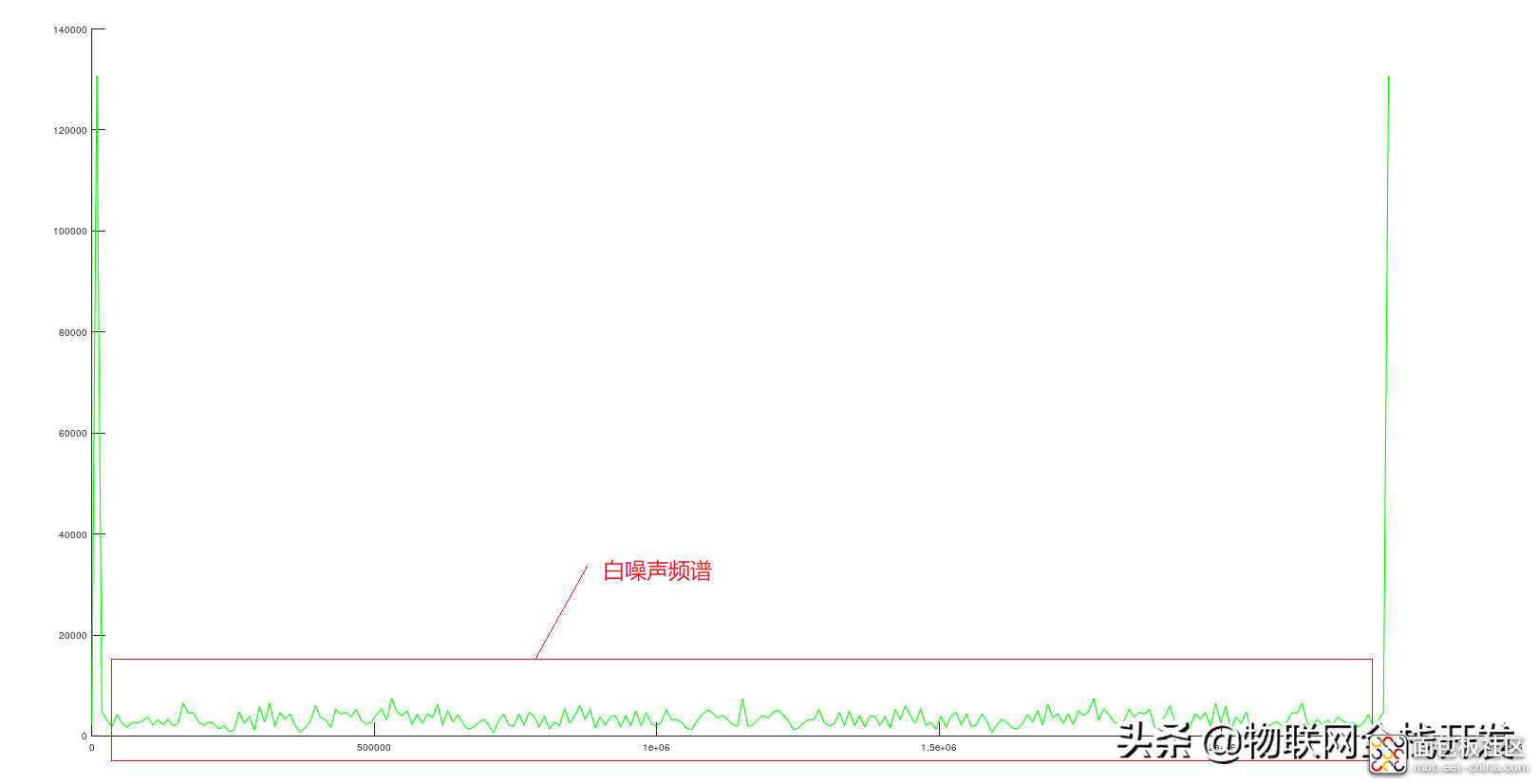
注入了高斯白噪声的信号频谱
可见, 白噪声的功率谱密度服从均匀分布。
可以通过以下公式估算出注入了噪声的正弦信号幅度ay':
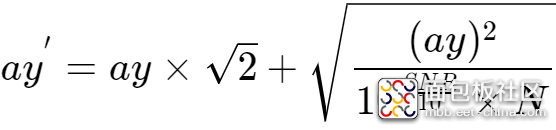
代入,ay=1000, SNR=10, N=256,得到:
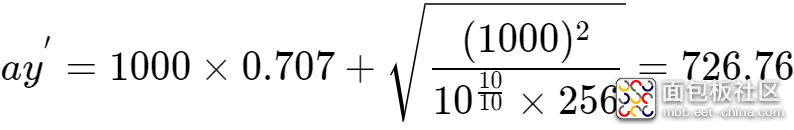
在幅度为1000的正弦信号的采样数据上叠加大小为(-50,50)之间的随机数。
得到如下图所示的含有随机噪声的波形,
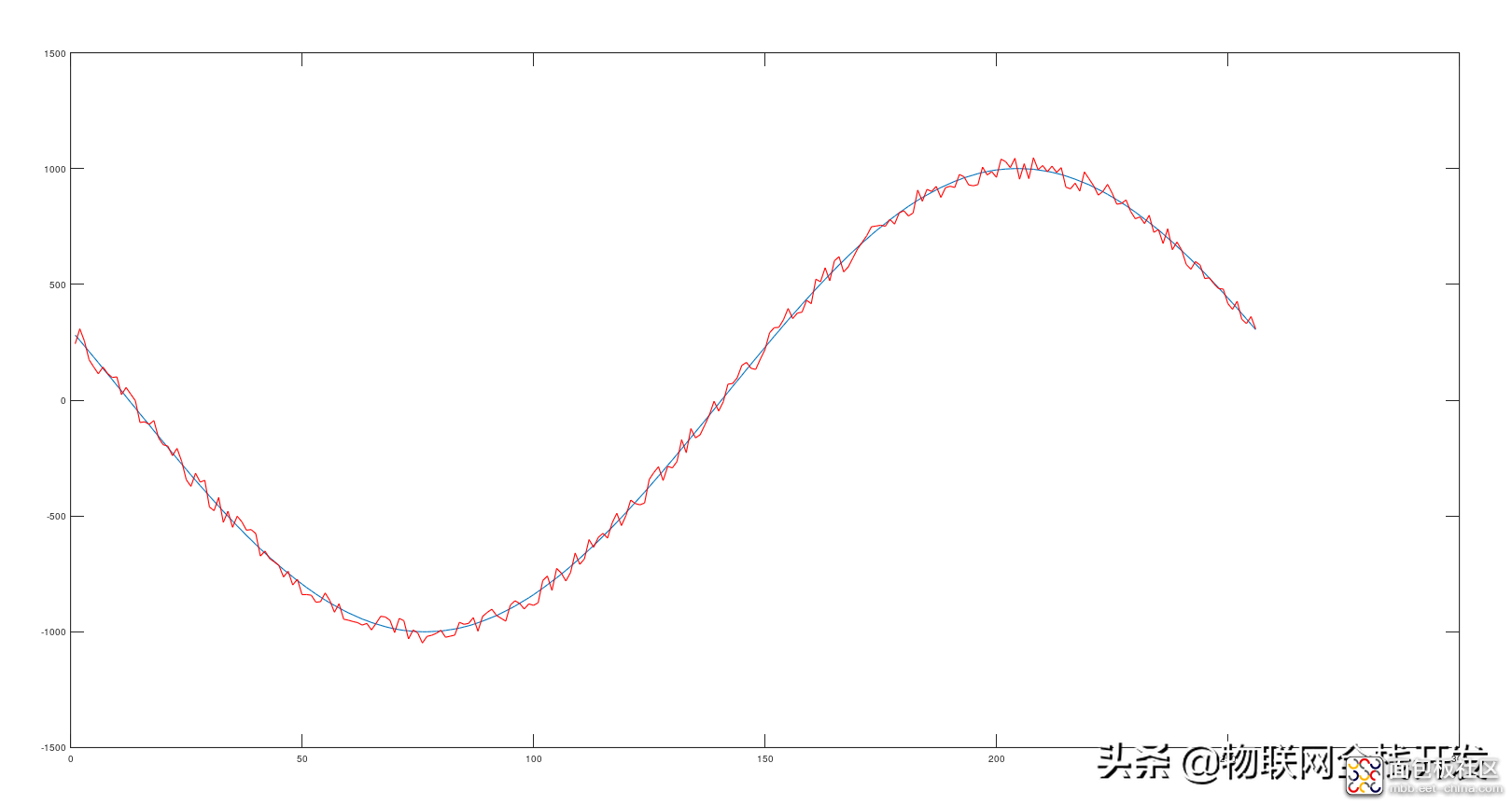
模拟生成的带噪声的正弦信号
此时,模拟信号的信噪比为26.0。
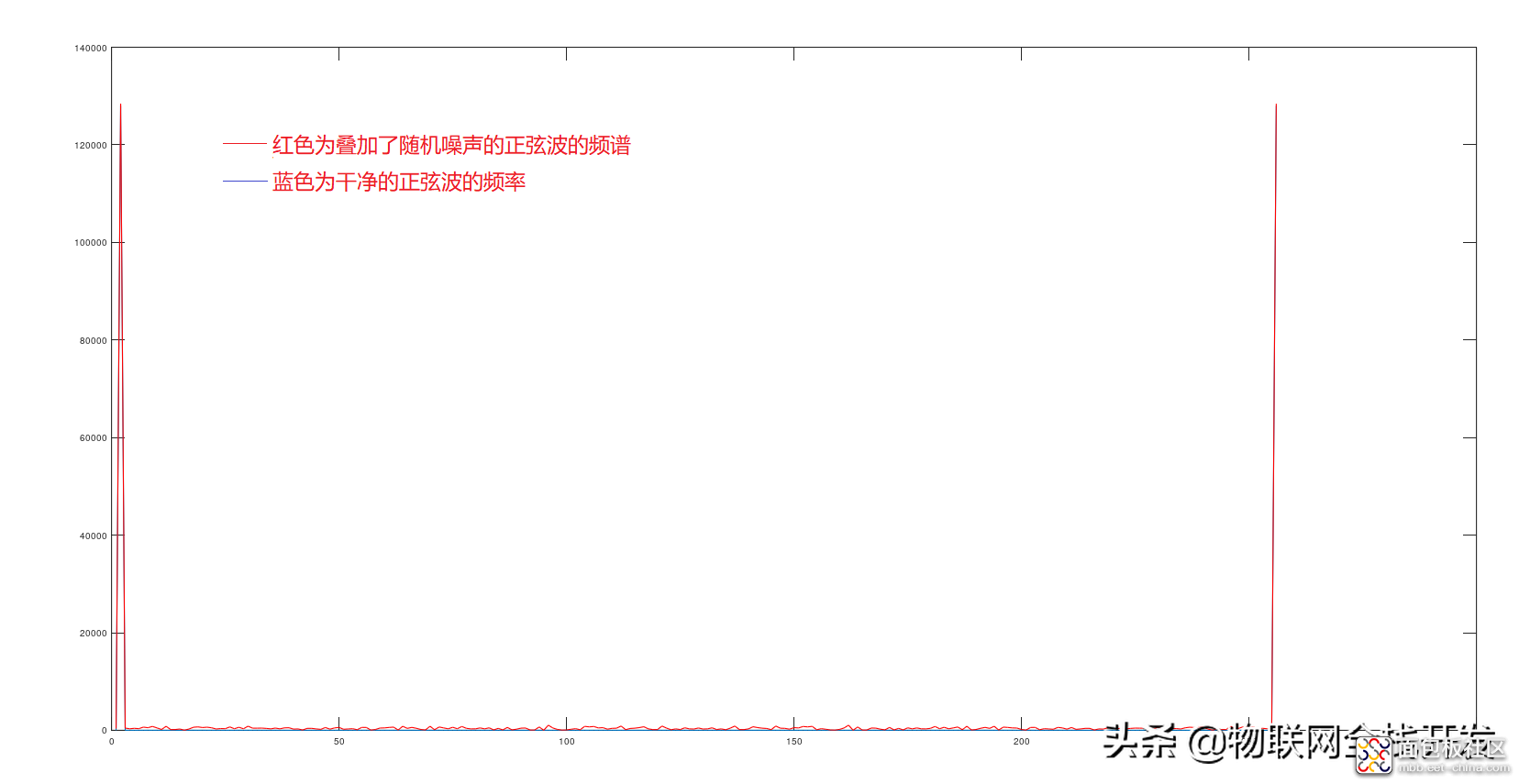
叠加了随机噪声的正弦波的频谱
将采样率设定为N倍的信号频率,
依次将N设定为2, 4, 8, 16, 32, 64, 128, 256。
对于每一个数值N,都注入上述随机噪声,按N倍的信号频率采样之后,在时域计算真有效值。
每一个N都模拟计算10000次,对10000次得到的真有效值进行统计分析得到平均值和标准偏差,得到结果如下:
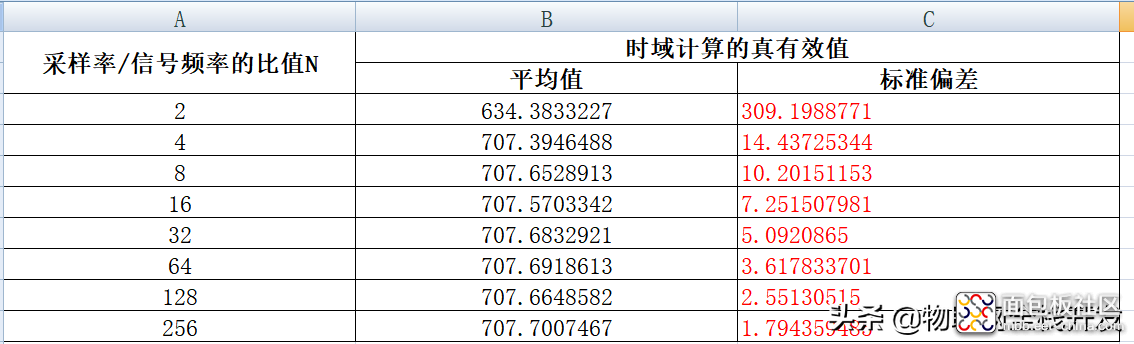
仿真计算结果
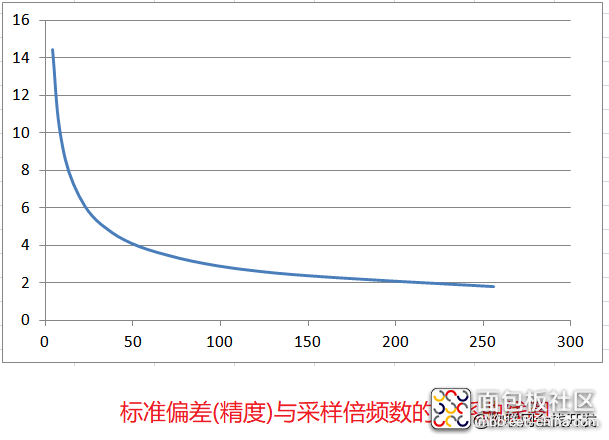
标准偏差与过采样倍频数的关系曲线图
结论
当采样率为信号频率的2倍时,计算得到的真有效值的统计结果,平均值与实际数值707相差比较大,而且标准偏差也比较,也就是即不准确也不精确,不能还原出原始信号。
当采样率大于信号频率的2倍时,计算得到的真有效值的统计结果,平均值与实际数值707相差不大,但是标准偏差随着采样率的增加而降低。
这就说明,虽然可以还原出原始信号,但是测量的精度随着采样率的增加而提高。
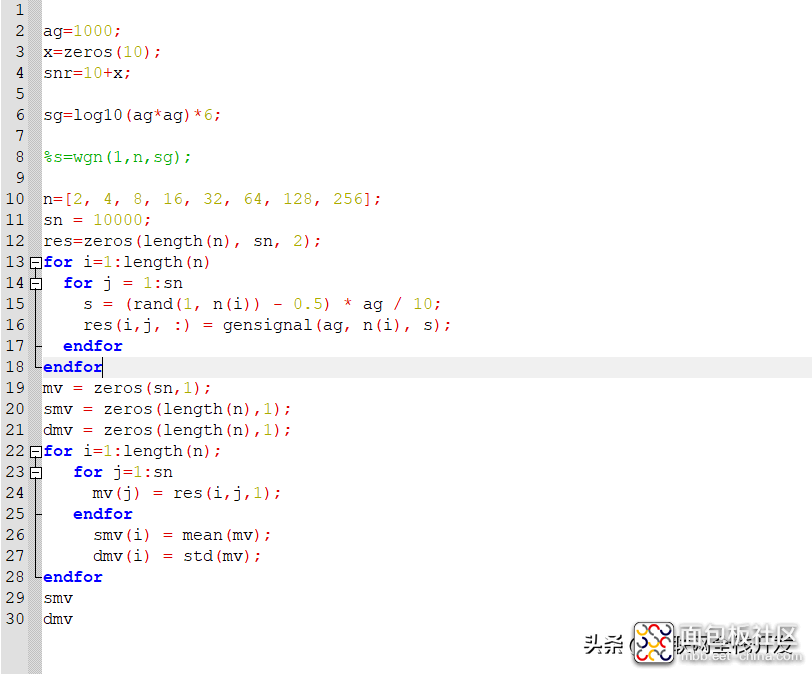
代码1
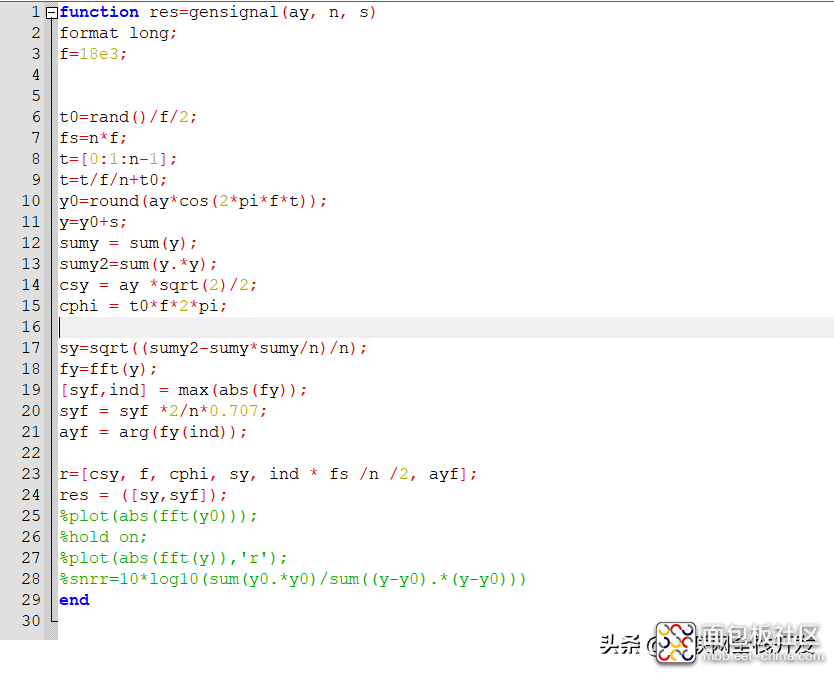
代码2
来源:物联网全栈开发






 /4
/4 

