课程概要 |
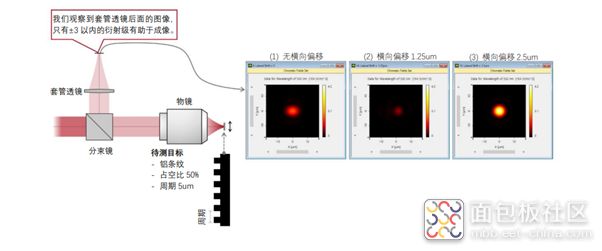
近年来,在材料学和生物学领域,对于微纳结构的成像,例如纳米小球,亚波长光栅,蛋白质分子等等,越来越受到极大关注。而对于微纳结构的成像,需要用到高数值孔径光学显微镜。由于微纳结构以及高数值孔径显微镜有着很大的矢量特性,所以传统的基于标量的成像理论已经不再适用。因此,对整个显微镜系统的矢量成像分析显得越来越迫切。 在本次课程中,我们首先介绍基于Debye-wolf 理论,对于偶极子(Dipole source)的理想高数值孔径的矢量点扩散函数的计算(vectorial PSF)。其次,我们会根据真实的显微镜系统来对Dipole Source 成像,分析矢量点扩散函数以及双螺旋(double helix)点扩散函数, 并分析不同光学系统的相差, 例如尼康(Nikon),奥林巴斯(Olympus),蔡司(Zeiss)等,以及实验中遇到的非准直等误差对结果的影响。再次我们会介绍严格麦克斯韦方程组解法,傅里叶模态法,用来对微纳结构做矢量模拟。最后,我们会结合透镜系统和微纳结构,讲解一些具体的显微镜系统应用及其成像质量分析,包括阿贝成像理论的实验,紫外显微镜对光栅的观察,晶圆级光学 (Wafer Level Optics) 对准装置的模拟,共聚焦扫描显微镜 (Scanning Confocal Microscopy) 成像原理的探究,傅里叶显微镜(Fourier Microscopy)对单分子的矢量成像,单光子结构光照明显微镜(Structured Illumination Microscopy)矢量照明分析,双光子(Two-photon)结构光照明显微镜的时域聚焦(temporal focusing)特性。 基于上述真实显微镜系统应用,我们还会和学员共同在现场利用VirtualLab Fusion完成模拟已经像差和物理原理的分析。 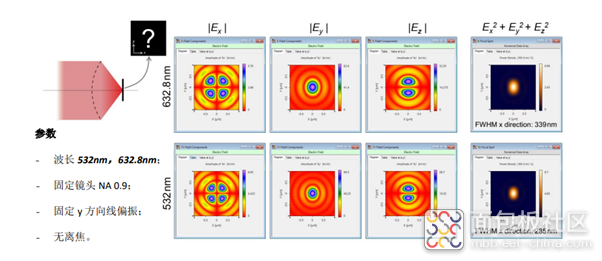
|
课程大纲 |
● 高数值孔径的理想透镜的矢量建模 利用Debye-Wolf积分来分析理想透镜的矢量成像特性,并辅以案例操作。 ● 高数值孔径的真实商业透镜的矢量建模 利用数值的计算的方法,快速计算求得带有像差和实验误差的矢量点扩散函数(PSF)以及双螺旋(double helix)点扩散函数的分布,并辅以案例操作。 ● 利用严格麦克斯韦方程解,傅里叶模态法对微纳光栅,微纳粒子进行建模。并辅以案例操作。 ● 傅里叶模态法对任意光束的建模,并辅以案例操作。 ● 利用矢量物理光学对 阿贝成像分辨率(Abbe Resolution) 的探究,紫外显微镜(UV microscopy)对于微纳结构的成像, 晶圆级光学 (Wafer Level Optics) 对准装置的模拟, 并辅以案例操作。 ● 利用矢量物理光学对共聚焦扫描显微镜 (Scanning Confocal Microscopy) 成像原理的探究,傅里叶显微镜(Fourier Microscopy)对单分子的矢量成像,并辅以案例操作。 ● 利用矢量物理光学对结构照明光显微镜(Structured Illumination Microscopy),高数值孔径时域聚焦研究, 双光子显微镜(Two-Photon Microscopy)的模拟和分析。 ● 利用VirtualLab Fusion案例操作:利用基于场追迹的矢量快速物理光学对结构照明光显微镜(Structured Illumination Microscopy)高数值孔径时域聚焦研究,双光子显微镜(Two-Photon Microscopy)的模拟和分析,并回答学员所有的问题。 课程安排 |





 /4
/4 

