在显微镜中，术语“分辨率”用于描述显微镜区分标本或样品细节的能力。换句话说，标本的两个不同点之间的最小距离，观察者或显微镜相机仍然可以将它们视为单独的实体。分辨率与显微镜光学元件（如物镜）的数值孔径（NA）以及所用光的波长有着内在的联系。本文介绍了解析概念背后的一些历史，并使用相对简单的术语解释了每个概念。

数值孔径（NA）与光通过的介质的折射率（n）以及给定物镜的角孔径（α）有关（NA = n sinα）。考虑到显微镜聚光镜的数值孔径，光学显微镜的分辨率不仅取决于物镜的数值孔径，还取决于整个系统的数值孔径。更多的图像细节将在显微镜系统中解析，其中所有光学组件都正确对齐，具有相对较高的NA值并且彼此和谐地工作。分辨率还与用于对标本成像的光的波长有关;较短波长的光能够比较长波长的光分辨更多的细节。

在处理分辨率时需要考虑 3 个数学概念：阿贝衍射极限、艾里斑和瑞利准则。下面按时间顺序介绍其中的每一个。

乔治·比德尔·艾里（1801-1892）是英国数学家和天文学家。到1826年（25岁），他被任命为三一学院的数学教授，两年后，他被任命为新剑桥天文台的天文学教授。从1835年到1881年，他是“皇家天文学家”，甚至有一个以他的名字命名的月球和火星陨石坑。

同样在1835年，他在《剑桥哲学学会学报》上发表了一篇题为“关于具有圆形孔径的物体玻璃的衍射”的论文[1]。艾里从天文学家的角度写了这篇论文，他在论文中描述了“在一台好的望远镜中看到的恒星图像周围的环或射线的形状和亮度”。尽管在不同的科学领域写作，但这些观察结果与包括显微镜在内的其他光学系统相关。

艾里斑是最佳聚焦的光点，可以通过受衍射限制的完美对齐系统中的圆形孔径来确定。从上面看（图1），这看起来像一个明亮的光点，周围是同心环或波纹（更准确地称为艾里图案）。

衍射图案由光的波长和光通过的孔径大小决定。艾里斑的中心点包含大约84%的发光强度，其余16%在该点周围的衍射图案中。当然，用显微镜观察的标本中有许多光点，与术语“艾里斑”所描述的单个光点相比，考虑许多艾里图案更为合适。

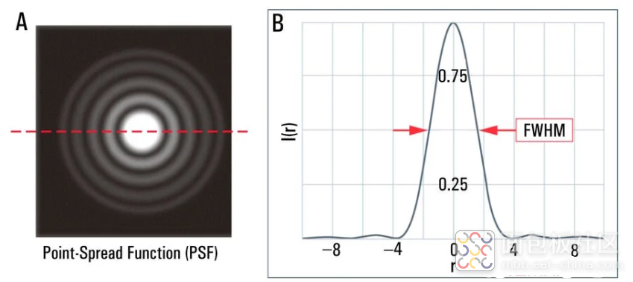
如图3右半部分所示的Airy图案的三维（1D）表示也称为“点扩散函数”（PSF）。

图 1 艾里图案的典型现象，也称为艾里斑，其中心最大光点和环绕的衍射环。

恩斯特·卡尔·阿贝（1840-1905）是德国数学家和物理学家。1866年，他遇到了卡尔·蔡司，他们一起创立了所谓的“蔡司光学工厂”，现在被称为蔡司。此外，他还于1884年共同创立了肖特玻璃厂。阿贝也是第一个定义数值孔径一词的人。1873年，阿贝发表了他的理论和公式，解释了显微镜的衍射极限[2]。Abbe认识到标本图像由许多重叠的，多强度的衍射极限点（或艾里斑）组成。

为了提高分辨率，d = λ/（2NA），必须使用较短波长（λ）的光或通过具有相对高折射率的成像介质或具有高NA的光学元件（或实际上，所有这些因素的组合）观察样品。

然而，即使考虑到所有这些因素，由于整个系统的复杂性、玻璃在400nm以下波长下的透射特性以及在整个显微镜系统中实现高数值孔径的挑战，使用真实显微镜的可能性仍然有限。理想光学显微镜的横向分辨率限制在200 nm左右，而轴向分辨率约为500 nm（分辨率限制示例如下）。

约翰·威廉·斯特鲁特，第三代瑞利男爵（1842-1919）是英国物理学家和多产作家。在他的一生中，他撰写了惊人的466篇出版物，包括430篇科学论文。他写了很多不同的主题，如鸟类飞行、心理研究、声学。1895年，他发现了氩（Ar），并于1904年获得诺贝尔物理学奖。

瑞利以乔治·艾里的工作为基础并扩展了他的工作，并于1896年发明了“瑞利准则”理论[3]。瑞利准则定义了衍射极限系统中的分辨率极限，换句话说，当两个光点可以区分或彼此分辨时。

使用艾里斑理论，如果来自两个单个艾里斑的衍射图案不重叠，那么它们很容易区分，“很好地解决”，并且据说符合瑞利准则。当一个艾里斑的中心与另一个衍射图的第一个最小值直接重叠时，它们可以被认为是“刚刚解决”的，并且仍然可以区分为两个独立的光点（图2，中间）。如果艾里斑比这更近，那么它们就不符合瑞利准则，并且“未解析”为两个不同的光点。

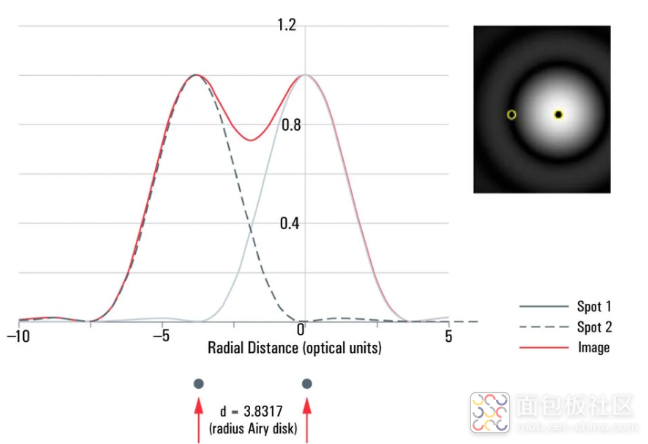
图 2对于瑞利准则，如果一个点的中心落在另一个点的 PSF 的第一个零（暗环）上，则认为 2 个斑点（插图中用黄色环标记的中心）已解决。该标准仅对类似艾里 PSF 有效。

更实用的分辨率方法是光学未分辨结构的半峰全宽（FWHM）强度[4，。该值相对容易用显微镜测量，并且已成为用于比较目的的普遍接受的参数。FWHM 的理论值为 R富华姆= 0.51λ/（NA），大约是λ/（2NA）。所以FWHM作为分辨率参数非常接近阿贝的衍射极限，但也可以从显微镜图像数据中测量。对于校准或分辨率极限测量，通常会对各种直径的磁珠或胶体进行成像和测量。

这些理论分辨率值源自物理和数学假设，是估计值。他们假设完美的成像系统和真空中的点光源或完全均匀的材料作为样品或样品。当然，这种假设在现实生活中几乎从未出现过，因为许多样品或标本都是异质的。由于只有有限量的光通过样品或从其表面反射，因此可测量的分辨率在很大程度上取决于信噪比（SNR）。

考虑到上述所有理论，很明显，在计算分辨率的理论极限时需要考虑许多因素。分辨率还取决于样品的性质。让我们看看使用阿贝衍射极限、瑞利准则和FWHM计算分辨率。

首先，应该记住：

NA = n（sinα）

其中n是成像介质的折射率，α是物镜角孔径的一半。物镜的最大角孔径约为144o。该角度的一半正弦是 0.95。如果使用折射率为1.52的油浸没物镜，则物镜的最大数值孔径为1.45。如果使用“干”（非浸没）物镜，物镜的最大数值孔径将为0.95（因为空气的折射率为1.0）。

横向（XY）分辨率的阿贝衍射公式为：

d = λ/（2NA），

其中λ是用于对标本成像的光波长。如果使用514 nm的绿光和数值孔径为1.45的油浸物镜，则（理论）分辨率极限将为177 nm。

轴向（Z）分辨率的阿贝衍射公式为：

d = 2λ/（NA）2

如果我们假设波长为514 nm来观察具有1.45 nm值的物镜的样品，那么轴向分辨率将为488 nm。

瑞利准则是基于阿贝衍射极限的略微改进的公式：

R = 1.22λ/（NAobj+ NAcond)

其中λ是用于对标本成像的光波长。NAobj是目标的NA。NAcond 是冷凝器的 NA。值“1.22”是一个常量。这是从瑞利关于贝塞尔函数的工作中衍生出来的。这些用于计算系统中的问题，例如波传播。

考虑到聚光镜的数值孔径，空气（折射率为1.0）通常是聚光镜和载玻片之间的成像介质。假设聚光镜的角孔径为144o，则NA待续值将等于 0.95。

如果使用 514 nm 的绿光、数值孔径为 1.45 的油浸物镜、数值孔径为 0.95 的聚光镜，则（理论）分辨率极限将为 261 nm。

如前所述，FWHM可以直接从PSF测量，也可以使用以下方法计算：

RFWHM= 0.51λ/（NA）。

再次使用514 nm的光波长和NA为1.45的物镜，则理论分辨率将为181 nm。该值非常接近从阿贝衍射极限计算出的横向分辨率。

如上所述，用于对标本成像的光波长越短，精细细节的解析就越多。因此，如果使用最短波长的可见光400 nm，油浸物镜的数值孔径为1.45，聚光镜的数值孔径为0.95，则R等于203纳米。

为了达到显微镜系统的最大理论分辨率，每个光学元件应具有可用的最高数值孔径（考虑到角孔径）。此外，使用较短波长的光观察标本将提高分辨率。最后，整个显微镜系统应正确对准。

分享自：吾爱光设