共栅放大电路的特点是:输入阻抗较低(kΩ级),输出阻抗一般(kΩ级),电压放大倍数为10左右。共栅放大电路的优点是高频性能比较好,而且是同相放大。但由于其输入阻抗低,一般不适合单独使用,而是在组合电路中配合其他放大级一起使用,用于改善高频性能。
共栅放大电路一般如下图所示:
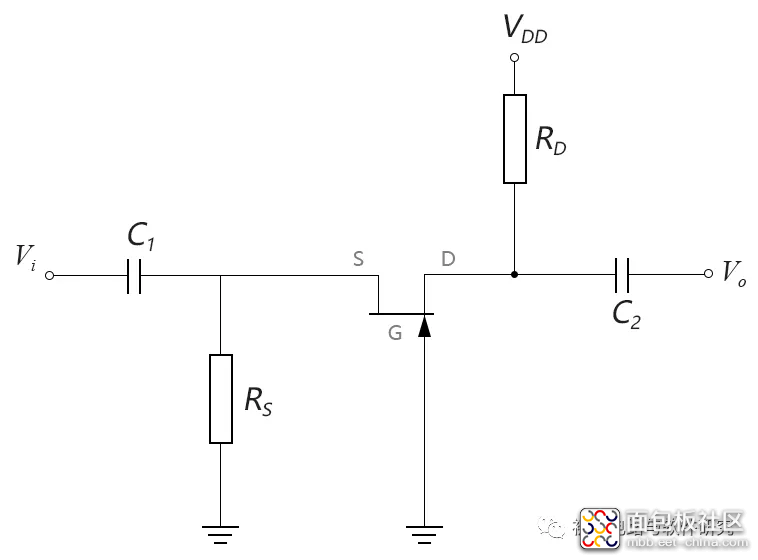
将上图中的电容C1、C2、CS视为短路,直流电压源视为直接通地,再代入JFET的交流等效电路,如下图所示:
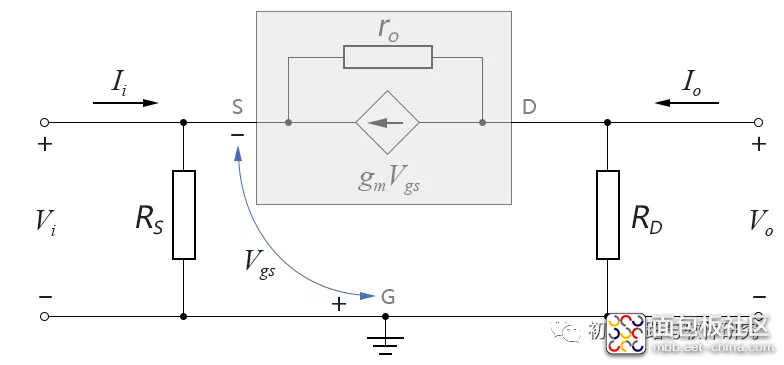
- 输入阻抗:
上图中的输入阻抗可视为RS与右侧部分的并联,设右侧部分的阻抗为Zi',则输入阻抗表达式为:
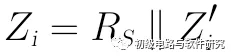
我们将右侧部分单独画出,如下图所示:
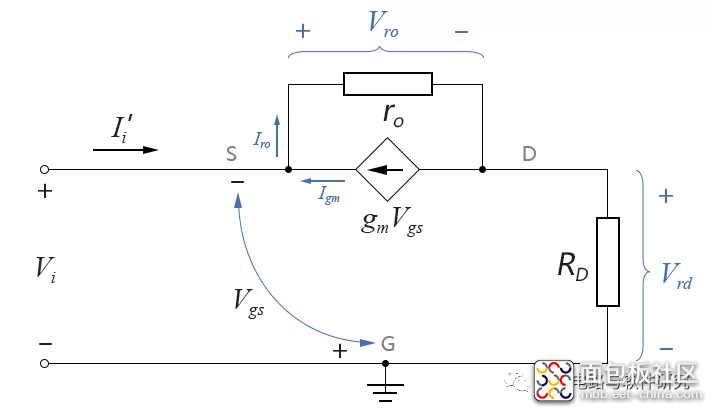
图中的Vro为电阻ro两侧电压,Vrd为电阻RD两侧电压;Iro和Igm分别为两个支路电流(注意图中的电压方向与电流方向都是人为定义方向,并不一定是实际的电压电流方向)。Vi的定义方向与Vgs相反,即:Vi = -Vgs。
首先可对上图应用基尔霍夫电压和电流定律,得到两个基本的电压电流关系式:
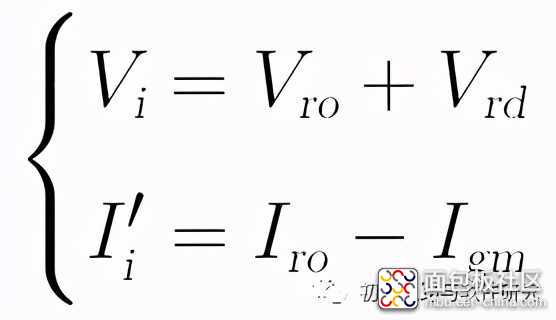
将其中的电压关系式展开可得:
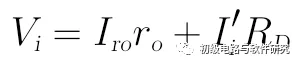
上式中的Iro可用电流关系式展开表示为:
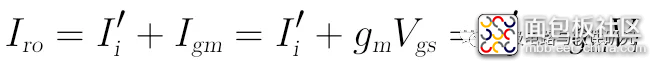
将这个Iro代入上面的电压关系展开式可得:
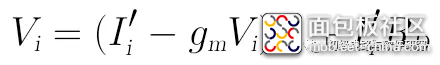
将上式中的Vi与Ii分别提取合并,可得:
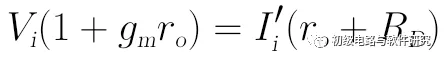
因此,上图7-3.03的输入阻抗为:
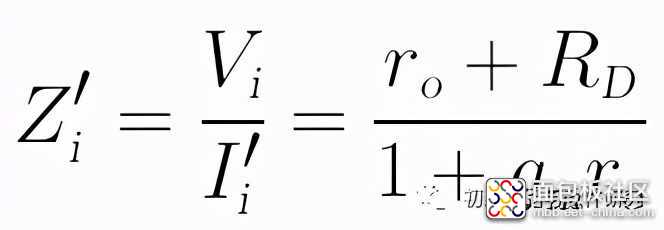
最终,总输入阻抗为:
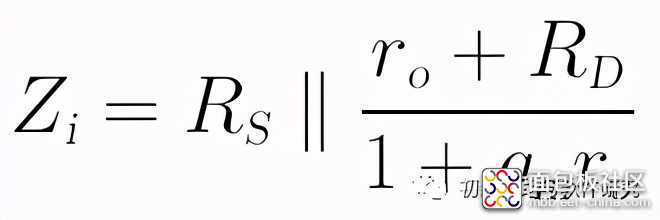
当ro远大于RD时,输入阻抗可近似为:
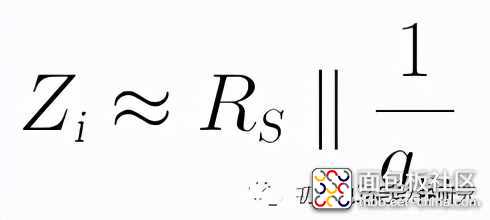
- 输出阻抗:
当将输入电压Vi置0时,受控电流源gmVgs=0,可视为开路,且RS被Vi短路,输出阻抗可简单看出为:
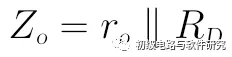
- 电压放大倍数:
电压放大倍数的计算可利用上面的图7-3.03来计算,我们将其重画于下,并标出Vo:
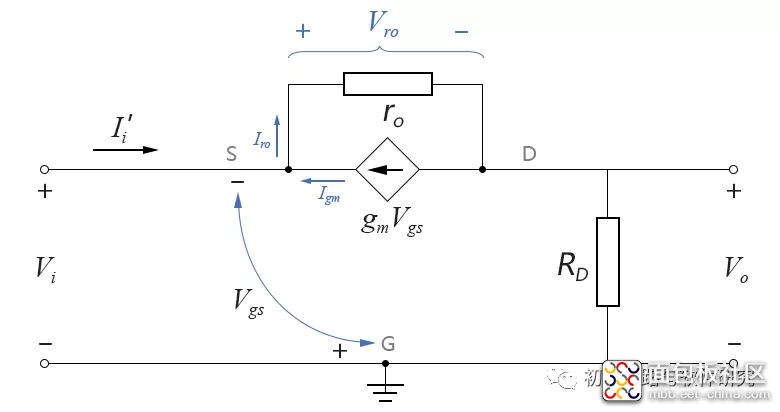
可利用Vo/Vi来求其空载电压放大倍数,我们先列写基尔霍夫电压方程:
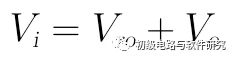
我们可利用在上面计算输入阻抗时得到的一些中间结果,作如下递推:
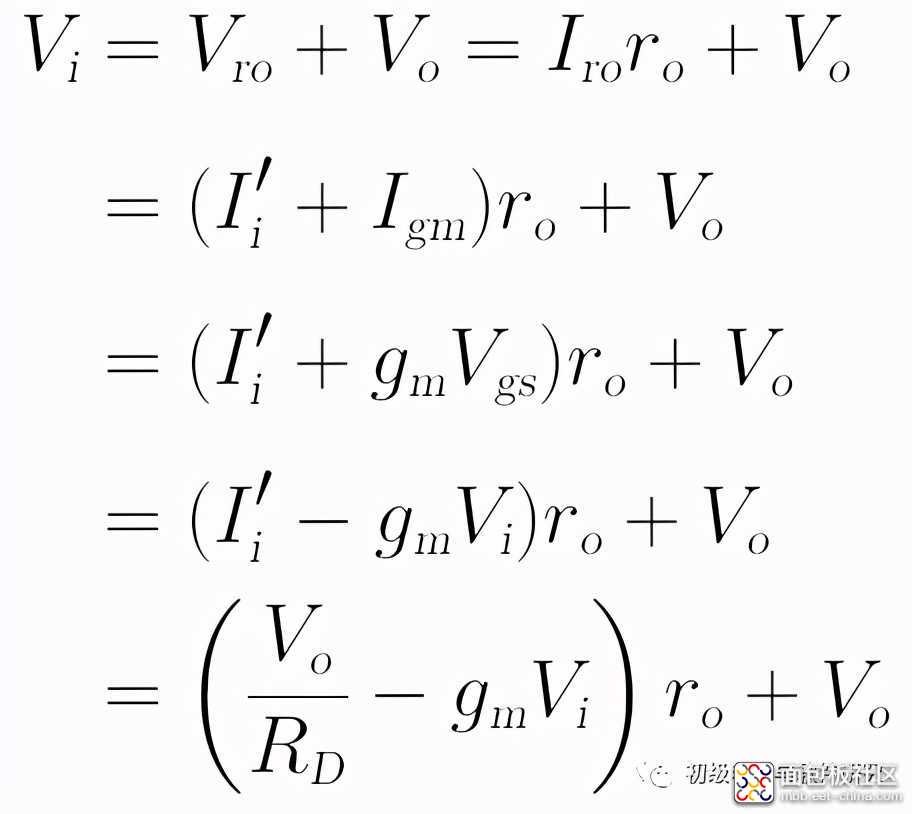
将上式中的Vi与Vo分别提取合并,可得:
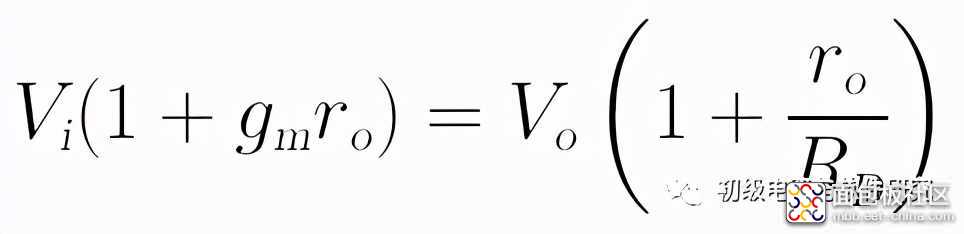
因此,电压放大倍数为:
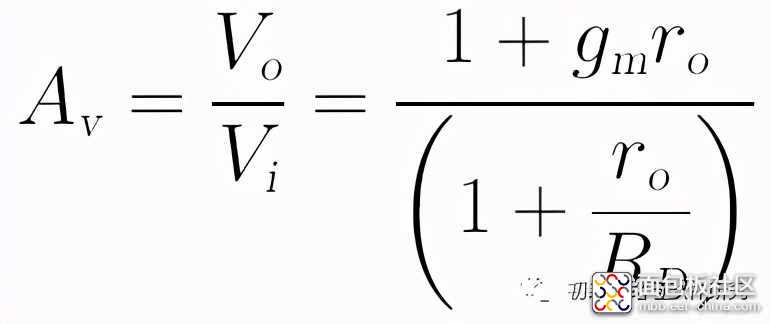
在ro远大于RD时,上式中分子和分母的中的1可省略,电压放大倍数可近似为:
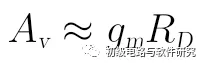
上式中Av的符号为正,表明共栅放大电路中,输出电压Vo和输入电压Vi同相。







 /2
/2 
