
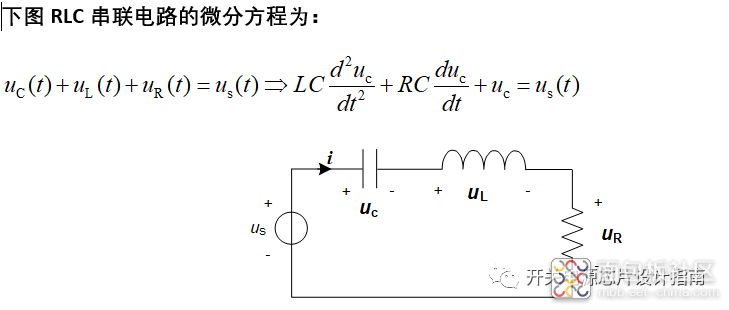


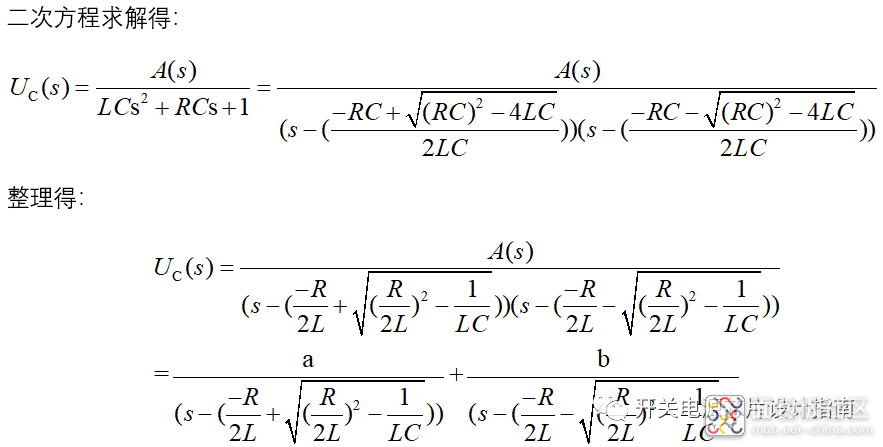

从上式可以看出,在有实数根时,电容电压uc(t)都是以自然对数e来无振荡衰减,分别是我们熟知的过阻尼振荡和临界阻尼振荡;当出现虚数根时uc(t)为欠阻尼振荡,上式根据欧拉公式进一步改写成如下形式,式中出现了正弦函数,可联想到欠阻尼的振荡波形,即该uc(t)波形的幅值为A以指数e(-R/2L)衰减,阻尼振荡角频率为w.
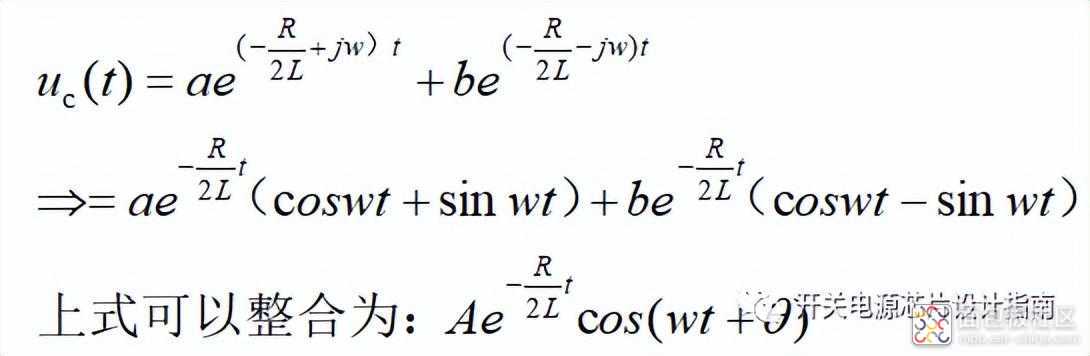
欠阻尼振荡特点是能量在电容和电感之间交换时,电流流过串联电阻,造成能量损失,形成衰减振荡;因此电阻越小,单位振荡周期消耗的能量越少,振荡幅值衰减越慢;当电阻R=0Ω时,电容电压uc(t)呈正弦等幅振荡。另外当电阻R固定时,电感量L越小,电容越大,越不容易发生欠阻尼振荡,可以理解为当电容C进行放电时,电感L存能少,不足以给电容反向充电形成振荡。
无源电流采样网络计算:电容C1的电压为带偏置的正弦电压,可以通过CS1和R1来对流过C1的电流进行采样.
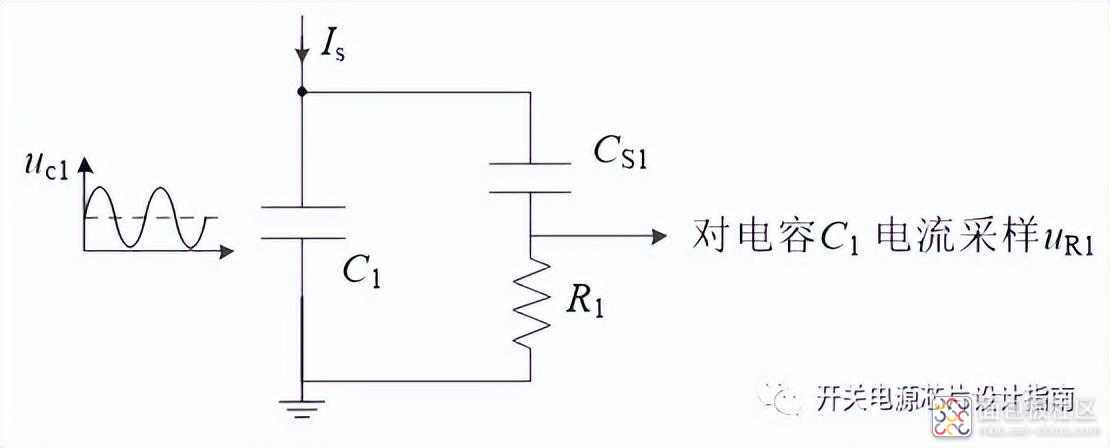
则电阻R1上的电压可以表示如下,理想情况下期望采样值与C1的电流相位一致,幅值按比例缩小。相位一致就需要式中sC1CS1R1=0,这样电流就可以按C1和CS1容值大小进行比例分配。以s=jw=j*2π*200kHz,C1=82nF为例,为了避免采样电路对主电路影响,一般取CS1/C1=0.01至0.001; 当Is=5cos(wt) A, CS1=100pF,R1=200Ω(合适的采样电压), sC1CS1R1=j2, 则采样电压可近似为UR1==200*(0.1/82.1)*5cos(wt)=1.21*cos(wt) V;
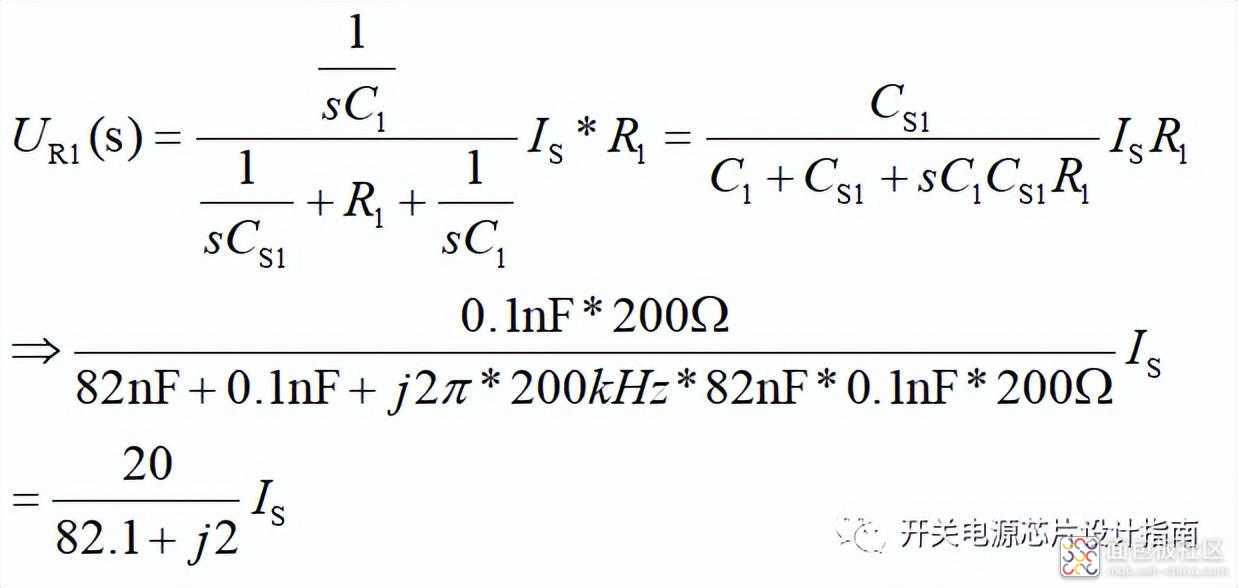
无源电压采样网络计算:电容C1的电压为带偏置的正弦电压,可以通过CS1和CS3来对C1的电压进行采样.
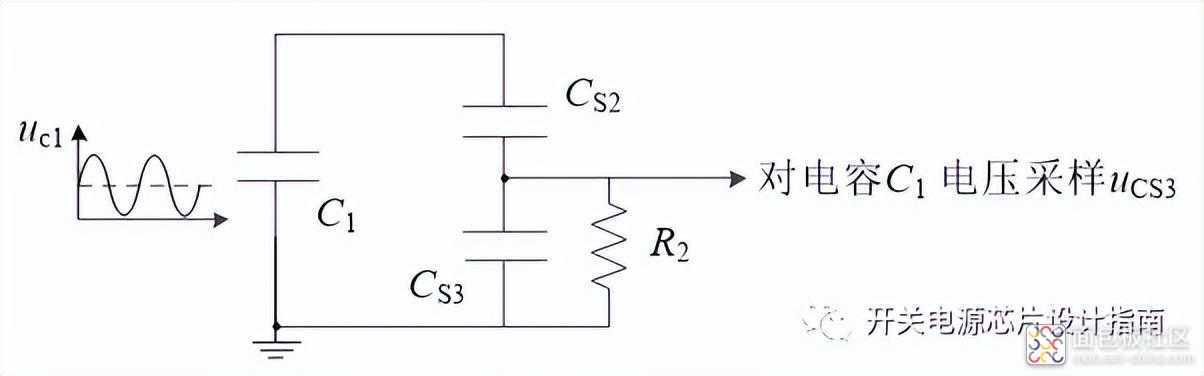
则电阻R2上的电压可以表示如下,理想情况下期望采样值的相位一致,幅值按比例缩小。相位一致就需要式中1/sR2为0,这样电压就可以按C1和CS1容值大小进行比例分配。同理,为了避免采样电路对主电路影响,取CS1=100pF; 当uC1=200sin(wt)+200V,R2必须为k Ω级才能忽略相位差;R2另一个作用时去除uC1的直流偏置,采样电路的时间常数为τ=R2(CS2+CS3)=16.4us;再直流偏置变化比较快时,为了滤除直流偏置的影响,需要减小R2来减小τ,此时采样相位误差会略有变大,采样幅值变小。








 /2
/2 
